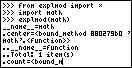
Module TI-Python: exploration module math + comparaisons
Cet article traite entre autres du module TI-Python, au sujet duquel il est rédigé a posteriori et illustré à l’aide des photos de tests prises sur le stand de Texas Instruments aux journées APMEP 2018 puis congrès UdPPC 2018. Nous ne disposons pas à ce jour du module.
Certaines photos ne correspondront pas exactement à ce qui est décrit, car nous avons amélioré le script utilisé entre les deux événements, sans pouvoir reprendre toutes les photos pour diverses contraintes lors du second événement.
Dans tous les cas, notez que ces tests ont été réalisés sur un prototype non final, et que des choses évoquées peuvent changer d'ici la livraison, en bien ou en mal d’ailleurs.
Certaines photos ne correspondront pas exactement à ce qui est décrit, car nous avons amélioré le script utilisé entre les deux événements, sans pouvoir reprendre toutes les photos pour diverses contraintes lors du second événement.
Dans tous les cas, notez que ces tests ont été réalisés sur un prototype non final, et que des choses évoquées peuvent changer d'ici la livraison, en bien ou en mal d’ailleurs.
 Dans un article précédent nous t'avons présenté le TI-Python, module externe permettant l'exécution de scripts Python sur ta TI-83 Premium CE, et t'avions annoncé la présence du module math. Par la suite, nous avions exploré son module builtins.
Dans un article précédent nous t'avons présenté le TI-Python, module externe permettant l'exécution de scripts Python sur ta TI-83 Premium CE, et t'avions annoncé la présence du module math. Par la suite, nous avions exploré son module builtins.Aujourd'hui, explorons son module math à l'aide du même script suivant :
- Code: Select all
#platforms: (0)TI-Nspire (1)NumWorks (2)Graph 90+E (3)Graph 75+E (4)TI-Python
plines=[29,12, 7, 9,11]
pcols =[53,99,509,32,32]
try:
import sys
try:
if sys.platform=='nspire': platform=0
if sys.platform=='TI-Python Adapter': platform=4
except: platform=3
except:
try:
import kandinsky
platform=1
except:
platform=2
nlines=plines[platform]
ncols=pcols[platform]
curline=0
def mprint(*ls):
global curline
st=""
for s in ls:
if not(isinstance(s,str)):
s=str(s)
st=st+s
stlines=1+int(len(st)/ncols)
if curline+stlines>=nlines:
input("Input to continue:")
curline=0
print(st)
curline+=stlines
def explmod(obj,hd="",obs="",reset=True):
global curline
if(reset): curline=0
c=0
for itm in sorted(dir(obj)):
c=c+1
try:
if obs=="":
try:
obs=obj.__name__
except:
obs=str(obj)
obs=obs[obs.find("'")+1:obs.rfind("'")]
its=obs+"."+str(itm)
itv=eval(its)
mprint(hd+str(itm)+"="+str(itv))
if itv!=obj:
c=c+explmod(itv,hd+".",its,False)
except:
mprint(hd+str(itm))
if c>0:
mprint(hd+"Total: "+str(c)+" item(s)")
return c
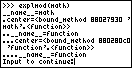
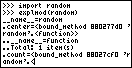
Le script nous liste alors pas moins de 50 entrées retranscrites ci-dessous :
TI-Python wrote:>>> from explmod import *
>>> import math
>>> explmod(math)
__name__='math'
.count()=<bound_method>
.endswith()=<bound_method>
.find()=<bound_method>
.format()=<bound_method>
.index()=<bound_method>
.isalpha()=<bound_method>
.isdigit()=<bound_method>.islower()=<bound_method>
.isspace()=<bound_method>
.isupper()=<bound_method>
.join()=<bound_method>
.lower()=<bound_method>
.lstrip()=<bound_method>
.replace()=<bound_method>
.rfind()=<bound_method>
.rindex()=<bound_method>
.rsplit()=<bound_method>.rstrip()=<bound_method>
.split()=<bound_method>
.startswith()=<bound_method>
.strip()=<bound_method>
.upper()=<bound_method>
Total: 22 item(s)
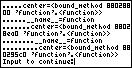
acos()=<function>
asin()=<function>
atan()=<function>
atan2()=<function>
ceil()=<function>
copysign()=<function>
cos()=<function>
degrees()=<function>
e=2.71828
exp()=<function>
fabs()=<function>
floor()=<function>
fmod()=<function>
frexp()=<function>isfinite()=<function>
isinf()=<function>
isnan()=<function>
ldexp()=<function>
log()=<function>
modf()=<function>pi=3.14159
pow()=<function>
radians()=<function>
sin()=<function>
sqrt()=<function>
tan()=<function>
trunc()=<function>
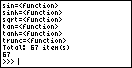
Total: 50 item(s)
50
>>>
Et bien comme tu vas le voir, ce n'est pas parce que deux calculatrices avec Python intègrent le module math qu'elles se valent. Voici ci-dessous la comparaison de ce que renvoient les différents modèles en lançant ce même script :
Casio Graph 90+E | NumWorks | TI-Python pour TI-83 Premium CE | ||
| __name__='math' acos() acosh() asin() asinh() atan() atan2() atanh() ceil() copysign() cos() cosh() degrees() e=2.718281828459045 erf() erfc() exp() expm1() fabs() floor() fmod() frexp() gamma() isfinite() isinf() isnan() ldexp() lgamma() log() log10() log2() modf() pi=3.141592653589793 pow() radians() sin() sinh() sqrt() tan() tanh() trunc() | __name__='math' acos() asin() atan() atan2() ceil() cos() e=2.718281828459045 exp() fabs() floor() fmod() frexp() ldexp() log() log10() modf() pi=3.141592653589793 pow() sin() sqrt() tan() trunc() | __name__='math' acos() asin() atan() atan2() ceil() copysign() cos() degrees() e=2.718281828459045 exp() fabs() floor() fmod() frexp() isfinite() isinf() isnan() ldexp() log() modf() pi=3.141592653589793 pow() radians() sin() sqrt() tan() trunc() | __name__='math' acos() acosh() asin() asinh() atan() atan2() atanh() ceil() copysign() cos() cosh() degrees() e=2.718281828459045 erf() erfc() exp() expm1() fabs() floor() fmod() frexp() gamma() isfinite() isinf() isnan() ldexp() lgamma() log() log10() log2() modf() pi=3.141592653589793 pow() radians() sin() sinh() sqrt() tan() tanh() trunc() | __name__='math' acos() asin() atan() atan2() ceil() copysign() cos() degrees() e=2.71828 exp() fabs() floor() fmod() frexp() isfinite() isinf() isnan() ldexp() log() modf() pi=3.14159 pow() radians() sin() sqrt() tan() trunc() |
| Total: 67 | Total: 47 | Total: 50 | Total: 63 | Total: 50 |
D'où le classement suivant :
- TI-Nspire avec 67 entrées
- NumWorks avec 63 entrées
- Casio Graph 35+E/75+E et module TI-Python pour TI-83 Premium CE avec 50 entrées
- Casio Graph 90+E avec 47 entrées
Les implémentations les plus complètes du module math concernent à ce jour de loin les NumWorks et TI-Nspire.
Les implémentations Casio Graph 90+E, Casio Graph 35/75+E et TI-Python pour TI-83 Premium CE à la différence ne retiennent que ce qui a été jugé utile à un niveau lycée par le ou les développeurs, avec quelques variations d'un modèle à un autre.
Outre l'absence de diverses fonctions dont les fonctions hyperboliques et logarithmes en base 2 et 10, notons que le module TI-Python semble également travailler sur des flottants en simple précision (32-bits), vu le nombre ridicule de décimales affichées pour les constantes de ce module...
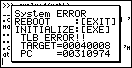
 ) du coup j'ai voulu savoir combien j'avais d'entrées, mais le script s'arrête à 26 (en exécutant extmod("math")) :
) du coup j'ai voulu savoir combien j'avais d'entrées, mais le script s'arrête à 26 (en exécutant extmod("math")) :