Correction algorithme Obligatoire BAC S 2013 (Antilles)
Intéressons-nous ce soir à l'algorithme tombé au sujet de Maths Obligatoire du BAC S 2013 en Antilles-Guyane, en exercice 4.
Il est assez particulier et donc intéressant; en effet il n'est pas seulement tombé avec une suite comme d'habitude, mais avec une suite complexe!

Question A)3)a)
On nous demande donc une trace de l'algorithme avec l'état des variables à chaque itération de la boucle (supposons que c'est à chaque fin d'itération de boucle - puisque l'énoncé ne précise pas).
Il nous suffit pour cela de traduire l'algorithme en un programme pour notre calculatrice TI-76/82/83/84:

Rajoutons maintenant une simple instruction de sortie dans la boucle...
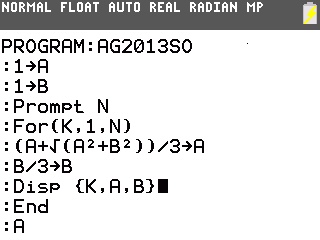
Et il n'y a plus qu'à recopier les résultats!

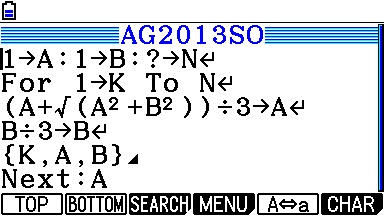
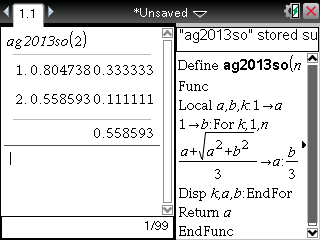
La même chose pouvait bien sûr s'obtenir à partir d'une Casio Graph/Prizm ou d'une TI-Nspire/89/92/V200:
Question A)3)b)
L'énoncé définit donc une suite complexe zn+1=(zn+|zn|)/3 avec z0=1+i.
Cette suite complexe peut être modélisée par deux suites réelles a et b prenant respectivement les valeurs des parties réelles et imaginaires:
an+1=(an+√(an2+bn2))/3 avec a0=1
bn+1=bn/3 avec b0=1
Ce sont ces suites qu'implémente l'algorithme, ces relations se retrouvant exactement dans les initialisations et affectations récurrentes sur A et B.
On pouvait aussi deviner en remarquant b1=1/3 dans la trace précédente.
Comme l'algorithme se termine par un affichage de A, son but est d'afficher an, ou encore la partie réelle de zn.
Lien:
BAC S 2013 - Annales des sujets inédits toutes matières et corrections
Il est assez particulier et donc intéressant; en effet il n'est pas seulement tombé avec une suite comme d'habitude, mais avec une suite complexe!


Question A)3)a)
On nous demande donc une trace de l'algorithme avec l'état des variables à chaque itération de la boucle (supposons que c'est à chaque fin d'itération de boucle - puisque l'énoncé ne précise pas).
Il nous suffit pour cela de traduire l'algorithme en un programme pour notre calculatrice TI-76/82/83/84:

Rajoutons maintenant une simple instruction de sortie dans la boucle...

Et il n'y a plus qu'à recopier les résultats!


| K | A | B |
| 1 | 0,8047 | 0,3333 |
| 2 | 0,5586 | 0,1111 |
La même chose pouvait bien sûr s'obtenir à partir d'une Casio Graph/Prizm ou d'une TI-Nspire/89/92/V200:


Question A)3)b)
L'énoncé définit donc une suite complexe zn+1=(zn+|zn|)/3 avec z0=1+i.
Cette suite complexe peut être modélisée par deux suites réelles a et b prenant respectivement les valeurs des parties réelles et imaginaires:
an+1=(an+√(an2+bn2))/3 avec a0=1
bn+1=bn/3 avec b0=1
Ce sont ces suites qu'implémente l'algorithme, ces relations se retrouvant exactement dans les initialisations et affectations récurrentes sur A et B.
On pouvait aussi deviner en remarquant b1=1/3 dans la trace précédente.
Comme l'algorithme se termine par un affichage de A, son but est d'afficher an, ou encore la partie réelle de zn.
Lien:
BAC S 2013 - Annales des sujets inédits toutes matières et corrections