ec 4 algèbre de boole
DownloadTélécharger
Actions
Vote :
ScreenshotAperçu
Informations
Catégorie :Category: mViewer GX Creator App HP-Prime
Auteur Author: iRePlaY
Type : Application
Page(s) : 6
Taille Size: 224.32 Ko KB
Mis en ligne Uploaded: 12/05/2018 - 13:49:11
Uploadeur Uploader: iRePlaY (Profil)
Téléchargements Downloads: 66
Visibilité Visibility: Archive publique
Shortlink : http://ti-pla.net/a1492797
Type : Application
Page(s) : 6
Taille Size: 224.32 Ko KB
Mis en ligne Uploaded: 12/05/2018 - 13:49:11
Uploadeur Uploader: iRePlaY (Profil)
Téléchargements Downloads: 66
Visibilité Visibility: Archive publique
Shortlink : http://ti-pla.net/a1492797
Description
Chapitre 4
ALGÈBRE DE BOOLE
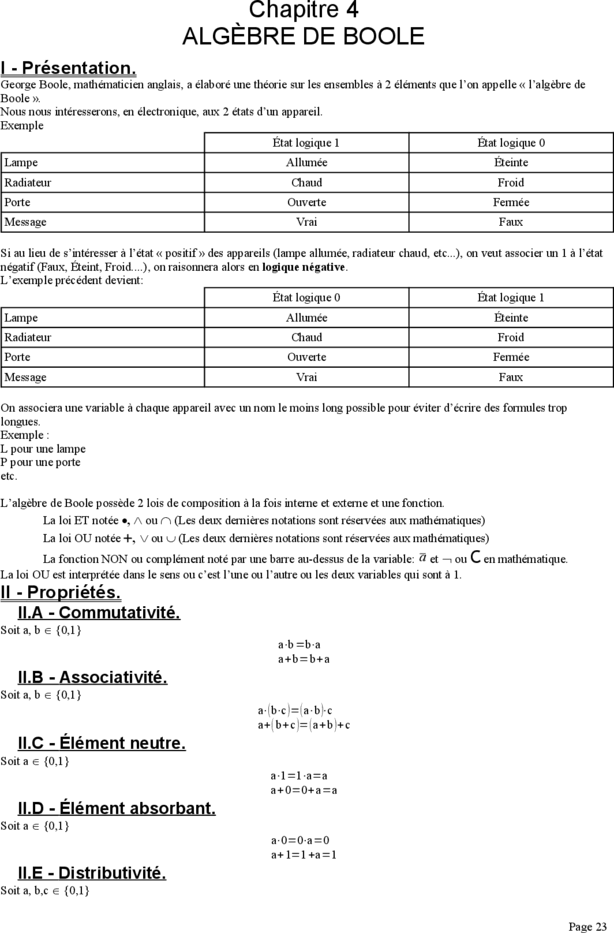
I - Présentation.
George Boole, mathématicien anglais, a élaboré une théorie sur les ensembles à 2 éléments que l’on appelle « l’algèbre de
Boole ».
Nous nous intéresserons, en électronique, aux 2 états d’un appareil.
Exemple
État logique 1 État logique 0
Lampe Allumée Éteinte
Radiateur Chaud Froid
Porte Ouverte Fermée
Message Vrai Faux
Si au lieu de s’intéresser à l’état « positif » des appareils (lampe allumée, radiateur chaud, etc...), on veut associer un 1 à l’état
négatif (Faux, Éteint, Froid....), on raisonnera alors en logique négative.
L’exemple précédent devient:
État logique 0 État logique 1
Lampe Allumée Éteinte
Radiateur Chaud Froid
Porte Ouverte Fermée
Message Vrai Faux
On associera une variable à chaque appareil avec un nom le moins long possible pour éviter d’écrire des formules trop
longues.
Exemple :
L pour une lampe
P pour une porte
etc.
L’algèbre de Boole possède 2 lois de composition à la fois interne et externe et une fonction.
La loi ET notée , Ù ou Ç (Les deux dernières notations sont réservées aux mathématiques)
La loi OU notée +, ou (Les deux dernières notations sont réservées aux mathématiques)
La fonction NON ou complément noté par une barre au-dessus de la variable: a et ou C en mathématique.
La loi OU est interprétée dans le sens ou c’est l’une ou l’autre ou les deux variables qui sont à 1.
II - Propriétés.
II.A - Commutativité.
Soit a, b {0,1}
a⋅b=b⋅a
a+b= b+a
II.B - Associativité.
Soit a, b {0,1}
a⋅( b⋅c )=( a⋅b)⋅c
a+( b+c )=( a+b )+c
II.C - Élément neutre.
Soit a {0,1}
a⋅1=1⋅a=a
a+0=0+a=a
II.D - Élément absorbant.
Soit a {0,1}
a⋅0=0⋅a=0
a+1=1 +a=1
II.E - Distributivité.
Soit a, b,c {0,1}
Page 23
Distributivité de par rapport à +
a⋅( b +c )=a⋅b+a⋅c
Distributivité de + par rapport à
a+( b⋅c )=( a+b )⋅( a+c)
ATTENTION, cette dernière propriété ne doit pas être utilisée en cours de mathématique pour un problème d’algèbre
classique
II.F - Propriétés de la fonction NON.
II.F.1 - Manipulation de la fonction NON.
Soit a, b,c {0,1}
̄a =a
On peut complémenter les deux membres d’une égalité
ā=b +c est identique à
̄a =b +c soit a= b+c
II.F.2 - Nilpotence.
Soit a {0,1}
a⋅ā =0
a+ ̄a =1
II.F.3 - Théorème de De Morgan.
Soit a, b {0,1}
a⋅b =̄a +̄b
a+b=̄a⋅̄b
II.F.4 - Idem-potence.
Soit a {0,1}
a+a=a
̄a + ̄a =̄a
a⋅a=a
̄a⋅̄a = ̄a
II.F.5 - Formule d’absorption.
Soit a, b {0,1}
a⋅(̄a +b) =a⋅b
a+ ̄a⋅b=a+b
II.F.6 - OU exclusif.
Soit a, b {0,1}
a b=a⋅̄b +̄a⋅b
a b=a⋅b+ā⋅̄b
III - Simplification de fonctions logiques.
Les propriétés développées ci-dessus permettent de simplifier des fonctions booléennes.
Exemples :
Simplifier les fonctions suivantes (noter les résultats) :
f ( a , b , c )=a⋅b⋅c+a⋅b⋅̄c +a⋅̄c =
f ( a , b , c )=a+b+c+a⋅b⋅̄c +a⋅̄c =
f ( a , b , c )=̄a⋅b⋅c+a⋅b⋅c+a+b=
f ( a , b , c )=a⋅̄c +a +b+c+a⋅b⋅c=
f ( a , b , c )=a⋅̄c +a⋅b⋅c+( a+b )⋅c=
f ( a , b , c )=( a +b)⋅( b+ ̄c ) +a⋅b+ ̄b⋅c=
Page 24
IV - Construction d’un logigramme.
L’objectif de la simplification est de construire un schéma électrique (logigramme) le plus simple possible.
Pour réaliser un schéma, on utilise des portes logiques:
Il existe des portes à 2, 3, 4 et 8 entrées.
Exemple :
Soit l’équation à simplifier suivante,
f ( a , b, c )=̄a⋅b⋅̄c +a⋅b⋅c+a⋅b
On trouve
f ( a , b , c )=̄a⋅c+ a⋅b + b c
On aura besoin de 2 portes ET à 2 entrées, un inverseur, une porte OU à 3 entrées et une porte OU exclusif à 2 entrées.
IV.A - Brochages des principales portes logiques (Utile dans un
simulateur).
Fonction Brochage TTL Brochage CMOS
OU NON à
2 entrées
OU NON à
3 entrées
Page 25
Fonction Brochage TTL Brochage CMOS
OU NON à
4 entrées
N’existe pas sous forme de porte simple.
ET NON à
2 entrées
ET NON à
3 entrées
ET NON à
4 entrées
OU à 2
entrées
OU à 3
entrées
N’existe pas sous forme de porte simple.
Page 26
Fonction Brochage TTL Brochage CMOS
OU à 4
entrées
N’existe pas sous forme de porte simple.
ET à 2
entrées
ET à 3
entrées
ET à 4
entrées
Amplificat
eur non
inverseur
N’existe pas sous forme de porte simple.
Page 27
Fonction Brochage TTL Brochage CMOS
Amplificat
eur
inverseur
OU
EXCLUSI
Fà2
entrées.
OU NON
EXCLUSI
Fà2
entrées
N’existe pas sous forme de porte simple.
ET NON à
8 entrées.
OU NON à
8 entrées.
N’existe pas sous forme de porte simple.
Page 28
ALGÈBRE DE BOOLE
I - Présentation.
George Boole, mathématicien anglais, a élaboré une théorie sur les ensembles à 2 éléments que l’on appelle « l’algèbre de
Boole ».
Nous nous intéresserons, en électronique, aux 2 états d’un appareil.
Exemple
État logique 1 État logique 0
Lampe Allumée Éteinte
Radiateur Chaud Froid
Porte Ouverte Fermée
Message Vrai Faux
Si au lieu de s’intéresser à l’état « positif » des appareils (lampe allumée, radiateur chaud, etc...), on veut associer un 1 à l’état
négatif (Faux, Éteint, Froid....), on raisonnera alors en logique négative.
L’exemple précédent devient:
État logique 0 État logique 1
Lampe Allumée Éteinte
Radiateur Chaud Froid
Porte Ouverte Fermée
Message Vrai Faux
On associera une variable à chaque appareil avec un nom le moins long possible pour éviter d’écrire des formules trop
longues.
Exemple :
L pour une lampe
P pour une porte
etc.
L’algèbre de Boole possède 2 lois de composition à la fois interne et externe et une fonction.
La loi ET notée , Ù ou Ç (Les deux dernières notations sont réservées aux mathématiques)
La loi OU notée +, ou (Les deux dernières notations sont réservées aux mathématiques)
La fonction NON ou complément noté par une barre au-dessus de la variable: a et ou C en mathématique.
La loi OU est interprétée dans le sens ou c’est l’une ou l’autre ou les deux variables qui sont à 1.
II - Propriétés.
II.A - Commutativité.
Soit a, b {0,1}
a⋅b=b⋅a
a+b= b+a
II.B - Associativité.
Soit a, b {0,1}
a⋅( b⋅c )=( a⋅b)⋅c
a+( b+c )=( a+b )+c
II.C - Élément neutre.
Soit a {0,1}
a⋅1=1⋅a=a
a+0=0+a=a
II.D - Élément absorbant.
Soit a {0,1}
a⋅0=0⋅a=0
a+1=1 +a=1
II.E - Distributivité.
Soit a, b,c {0,1}
Page 23
Distributivité de par rapport à +
a⋅( b +c )=a⋅b+a⋅c
Distributivité de + par rapport à
a+( b⋅c )=( a+b )⋅( a+c)
ATTENTION, cette dernière propriété ne doit pas être utilisée en cours de mathématique pour un problème d’algèbre
classique
II.F - Propriétés de la fonction NON.
II.F.1 - Manipulation de la fonction NON.
Soit a, b,c {0,1}
̄a =a
On peut complémenter les deux membres d’une égalité
ā=b +c est identique à
̄a =b +c soit a= b+c
II.F.2 - Nilpotence.
Soit a {0,1}
a⋅ā =0
a+ ̄a =1
II.F.3 - Théorème de De Morgan.
Soit a, b {0,1}
a⋅b =̄a +̄b
a+b=̄a⋅̄b
II.F.4 - Idem-potence.
Soit a {0,1}
a+a=a
̄a + ̄a =̄a
a⋅a=a
̄a⋅̄a = ̄a
II.F.5 - Formule d’absorption.
Soit a, b {0,1}
a⋅(̄a +b) =a⋅b
a+ ̄a⋅b=a+b
II.F.6 - OU exclusif.
Soit a, b {0,1}
a b=a⋅̄b +̄a⋅b
a b=a⋅b+ā⋅̄b
III - Simplification de fonctions logiques.
Les propriétés développées ci-dessus permettent de simplifier des fonctions booléennes.
Exemples :
Simplifier les fonctions suivantes (noter les résultats) :
f ( a , b , c )=a⋅b⋅c+a⋅b⋅̄c +a⋅̄c =
f ( a , b , c )=a+b+c+a⋅b⋅̄c +a⋅̄c =
f ( a , b , c )=̄a⋅b⋅c+a⋅b⋅c+a+b=
f ( a , b , c )=a⋅̄c +a +b+c+a⋅b⋅c=
f ( a , b , c )=a⋅̄c +a⋅b⋅c+( a+b )⋅c=
f ( a , b , c )=( a +b)⋅( b+ ̄c ) +a⋅b+ ̄b⋅c=
Page 24
IV - Construction d’un logigramme.
L’objectif de la simplification est de construire un schéma électrique (logigramme) le plus simple possible.
Pour réaliser un schéma, on utilise des portes logiques:
Il existe des portes à 2, 3, 4 et 8 entrées.
Exemple :
Soit l’équation à simplifier suivante,
f ( a , b, c )=̄a⋅b⋅̄c +a⋅b⋅c+a⋅b
On trouve
f ( a , b , c )=̄a⋅c+ a⋅b + b c
On aura besoin de 2 portes ET à 2 entrées, un inverseur, une porte OU à 3 entrées et une porte OU exclusif à 2 entrées.
IV.A - Brochages des principales portes logiques (Utile dans un
simulateur).
Fonction Brochage TTL Brochage CMOS
OU NON à
2 entrées
OU NON à
3 entrées
Page 25
Fonction Brochage TTL Brochage CMOS
OU NON à
4 entrées
N’existe pas sous forme de porte simple.
ET NON à
2 entrées
ET NON à
3 entrées
ET NON à
4 entrées
OU à 2
entrées
OU à 3
entrées
N’existe pas sous forme de porte simple.
Page 26
Fonction Brochage TTL Brochage CMOS
OU à 4
entrées
N’existe pas sous forme de porte simple.
ET à 2
entrées
ET à 3
entrées
ET à 4
entrées
Amplificat
eur non
inverseur
N’existe pas sous forme de porte simple.
Page 27
Fonction Brochage TTL Brochage CMOS
Amplificat
eur
inverseur
OU
EXCLUSI
Fà2
entrées.
OU NON
EXCLUSI
Fà2
entrées
N’existe pas sous forme de porte simple.
ET NON à
8 entrées.
OU NON à
8 entrées.
N’existe pas sous forme de porte simple.
Page 28













