BTS IRIS corrigé physique appliquée
DownloadTélécharger
Actions
Vote :
ScreenshotAperçu
Informations
Catégorie :Category: mViewer GX Creator Lua TI-Nspire
Auteur Author: skynet_360rg
Type : Classeur 3.6
Page(s) : 5
Taille Size: 363.77 Ko KB
Mis en ligne Uploaded: 30/03/2015 - 08:16:35
Uploadeur Uploader: skynet_360rg (Profil)
Téléchargements Downloads: 44
Visibilité Visibility: Archive publique
Shortlink : http://ti-pla.net/a179992
Type : Classeur 3.6
Page(s) : 5
Taille Size: 363.77 Ko KB
Mis en ligne Uploaded: 30/03/2015 - 08:16:35
Uploadeur Uploader: skynet_360rg (Profil)
Téléchargements Downloads: 44
Visibilité Visibility: Archive publique
Shortlink : http://ti-pla.net/a179992
Description
BTS IRIS PHYSIQUE APPLIQUEE 2013
CORRECTION
Partie A
16,5pts A.I.1. Charge de la batterie
P
A.I.1.1. Rappel : I . Voir document réponse 1 :
1pt U
P1 = 60W P1 = 120W P1 = 350W
0,5pt U1 = 44V U1 = 44V U1 = 44V
I1 = 1,36A I1 = 2,73A I1 = 7,95A
1pt A.I.1.2. Imax_charge = 2,9A pour la batterie 3. Il faut donc utiliser la puissance P2 = 120W
qui donne un courant de charge de 2,73A.
400W .h
1pt A.I.1.3. tch arg e 3,33h , soit 3h 20min c'est-à-dire 200 minutes.
120W
A.I.2. Décharge de la batterie
A.I.2.1. Le courant de décharge maximum est de 35A sous 44V soit une puissance maximum
1pt
400Wh
de 1540W. On a donc tdéch arg e 0,26h soit 15min et 35sec.
1540W
1pt A.I.2.2. T = 60s.
1 1
A.I.2.3. f = 16,7mHz.
1pt T 60
A.I.2.4. I
(12 10) (12 5) (12 10) 12 25 = 5A.
0,5pt 60 60
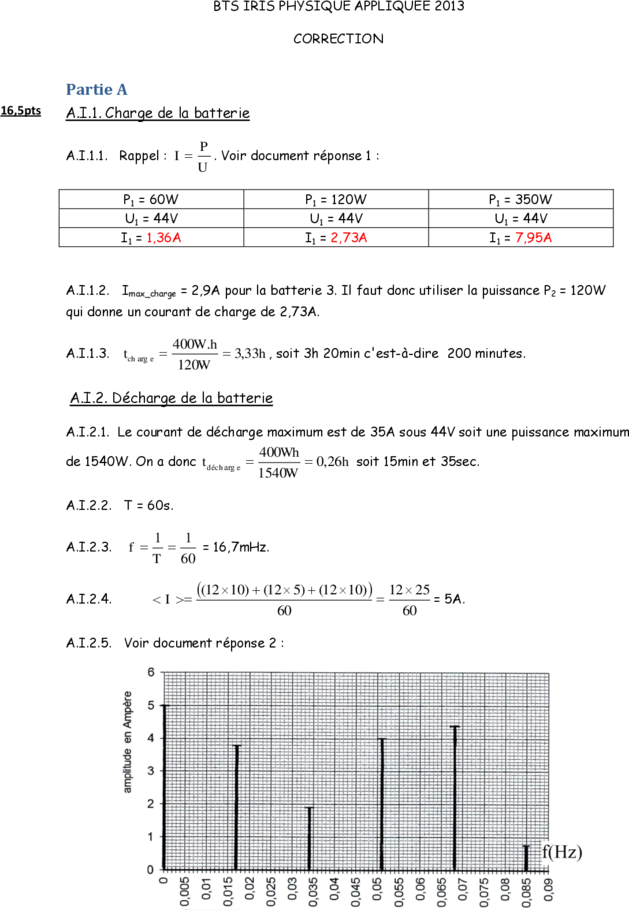
A.I.2.5. Voir document réponse 2 :
4pts
1,5pts
0,5pt
A.I.2.6. La fréquence la plus élevée est de 0,085Hz ; le rang correspondant est donc
0,085
5 (0,017Hz correspond à la fréquence du fondamental).
0,017
3,8² 1,9² 4² 4,4² 0,76²
A.I.2.7. On a I 5² = 7,21A.
2
A.I.2.8.
19,5pts Partie B
B.I. Mesure de la tension batterie
R12
B.I.1. Le pont diviseur de tension permet d’écrire : U12 .U BAT ;
R11 R12
1pt
B.I.2. l’amplificateur (AIL) fonctionne en linéaire grâce à la contre réaction, on peut
écrire U (t ) U (t ) ; comme U U12 et U U MES on a donc U MES U12 .
1pt
U MES R12 4,09
B.I.3. ; d’où 54.R12 = 4,09.R11 + 4,09.R12 4,09.R11 = 49,91.R12
U BAT R11 R12 54
R11 = 12,2.R12 R11 ≈ 1M.
1pt B.II. Mesure de l’intensité du courant
B.II.1. u1 max .imax = 0,001 × 50 = 50mV.
1pt us max 5
B.II.2. Il faut prendre A 100 .
u1 max 0,05
B.III. Caractéristiques de l’amplificateur
B.III.1. Le gain maximum est GMAX = +40dB ; l’amplification maximum est donc
GMAX 40
2pts AMAX 10 20
10 20
100 .
B.III.2. La bande passante correspond à la plage de fréquences pour lesquelles le gain
est supérieur ou égal à GMAX – 3dB ; ici, fC ≈ 1kHz ; la bande passante est donc [0 ;1kHz].
B.III.3. L’amplificateur à le comportement d’un filtre passe bas car le gain est
0,5pt maximum en continu et tend vers -∞ en hautes fréquences.
B.III.4. f = 50Hz, G = OdB ; f = 500Hz, G = -40dB ; l’atténuation est donc de
40dB/décade.
1pt B.III.5. Filtre du second ordre (40 = 2 × 20).
B.III.6. Ce filtre laisse passer la composante continue car son gain est maximal en
continu.
B.III.7. L’harmonique de rang le plus élevé est amplifiée par 100 (de la même façon que
la composante continue) car le gain est toujours de 40dB à 0,085Hz. On peut donc dire
que toutes les composantes harmoniques sont transmises.
B.III.8. Pour i = 12A, uS = ×A×12=0,001×100×12=1,2V.
B.III.9. Voir document réponse 3 :
18pts Partie C
C.I.
C.I.1. ( p) k RTH p ( p) RTH G( p) ; ( p).1 k RTH p RTH G( p) ;
1pt RTH
( p) G ( p) .
.1 k RTH p
1pt C.I.2. T0 = RTH et = k.RTH .
0,113
C.I.3. T0 = RTH = 0,113 et = k.RTH = 35,4 × 0,113 = 4s . D’où ( p) G( p)
.1 4 p
C.II. Réponse indicielle
1pt
531
C.II.1. G ( p)
p
1pt
0,113 531 60
C.II.2. ( p)
.1 4 p p p1 4 p
C.II.3. (t ) 60.1 e
t
2pts 60
C.II.4. lim (t ) lim p. ( p) lim p = 60°C
t p 0 p 0
p1 4 p
C.III.
C.III.1. Système du premier ordre : tangente à l’origine oblique.
C.III.2. 3 = 80°C ; ne correspond pas à l’essai de la question C.II car la température
en régime permanent n’est pas de 60°C.
C.III.3. Pour t = tr5% , = 0,63×60 = 37,8°C ; tr5% ≈ 7,5s.
C.III.4. La courbe qui correspond à l’essai de la question C.II est la courbe 1 car elle
donne = 4s et 1 max = 60°C.
C.III.5. = 60°C ; R () 60C
C.III.6. tr5% = 12s (pour 1 = 0,95 × 60 = 57°C)
26pts Partie D
D.I. Conditions d’acquisition
D.I.1. On a 30 échantillons pour 60s, soit 1 échantillon toutes les deux secondes ;
1 1
1pt fE = 0,5Hz.
TE 2
fE
1pt D.I.2. f max = 0,25Hz.
2
D.I.3. Oui, fE remplit la condition de Shannon car la fréquence maximum à traiter est
fE
inférieure à .
2
1pt D.II. Conversion analogique-numérique
D.II.1. nMAX = 2n – 1 = 28 – 1 = 255
1pt
U PE 4 4
D.II.2. On a q n
8 15,6mV
2 2 256
D.II.3. tC < TE
uS 1
D.II.4. N10 = = 64. N2 = 0100 0000
2pts q 15,625 103
0,5pt
D.III. Traitement numérique
D.III.1. Il s’agit d’un algorithme récursif car la sortie à l’instant n dépend de la
sortie à l’instant (n-1).
D.III.2.
D.III.3. Voir document réponse 4 :
n -1 0 1 2 3 4 5 6 7 8
xn 0 1 0 0 0 0 0 0 0 0
xn-1 0 0 1 0 0 0 0 0 0 0
yn-1 0 0 0 88 88 88 88 88 88 88
yn 0 0 88 88 88 88 88 88 88 88
D.III.4.
D.III.5. Le système numérique est stable car sa réponse impulsionnelle tend vers une valeur
finie.
D.III.6. On a yn 88xn1 yn1 ; la transformation en z donne : Y z 88.z 1. X z z 1.Y z ;
Y z 88.z 1
soit Y z . 1 z 1 88.z 1. X z ;
X z 1 z 1
; en multipliant par z le numérateur et le
Y z 88
dénominateur, on obtient .
X z z 1
X z
64 64 z
D.III.7.
1 z z 1
1
Y z
88 64 z 5632.z
D.III.8. .
z 1 z 1 z 12
D.III.9. Séquence rampe : yn = 5632.n
D.III.10. Energie = puissance × temps ; si la puissance est constante alors l’énergie augmente
linéairement avec le temps.
CORRECTION
Partie A
16,5pts A.I.1. Charge de la batterie
P
A.I.1.1. Rappel : I . Voir document réponse 1 :
1pt U
P1 = 60W P1 = 120W P1 = 350W
0,5pt U1 = 44V U1 = 44V U1 = 44V
I1 = 1,36A I1 = 2,73A I1 = 7,95A
1pt A.I.1.2. Imax_charge = 2,9A pour la batterie 3. Il faut donc utiliser la puissance P2 = 120W
qui donne un courant de charge de 2,73A.
400W .h
1pt A.I.1.3. tch arg e 3,33h , soit 3h 20min c'est-à-dire 200 minutes.
120W
A.I.2. Décharge de la batterie
A.I.2.1. Le courant de décharge maximum est de 35A sous 44V soit une puissance maximum
1pt
400Wh
de 1540W. On a donc tdéch arg e 0,26h soit 15min et 35sec.
1540W
1pt A.I.2.2. T = 60s.
1 1
A.I.2.3. f = 16,7mHz.
1pt T 60
A.I.2.4. I
(12 10) (12 5) (12 10) 12 25 = 5A.
0,5pt 60 60
A.I.2.5. Voir document réponse 2 :
4pts
1,5pts
0,5pt
A.I.2.6. La fréquence la plus élevée est de 0,085Hz ; le rang correspondant est donc
0,085
5 (0,017Hz correspond à la fréquence du fondamental).
0,017
3,8² 1,9² 4² 4,4² 0,76²
A.I.2.7. On a I 5² = 7,21A.
2
A.I.2.8.
19,5pts Partie B
B.I. Mesure de la tension batterie
R12
B.I.1. Le pont diviseur de tension permet d’écrire : U12 .U BAT ;
R11 R12
1pt
B.I.2. l’amplificateur (AIL) fonctionne en linéaire grâce à la contre réaction, on peut
écrire U (t ) U (t ) ; comme U U12 et U U MES on a donc U MES U12 .
1pt
U MES R12 4,09
B.I.3. ; d’où 54.R12 = 4,09.R11 + 4,09.R12 4,09.R11 = 49,91.R12
U BAT R11 R12 54
R11 = 12,2.R12 R11 ≈ 1M.
1pt B.II. Mesure de l’intensité du courant
B.II.1. u1 max .imax = 0,001 × 50 = 50mV.
1pt us max 5
B.II.2. Il faut prendre A 100 .
u1 max 0,05
B.III. Caractéristiques de l’amplificateur
B.III.1. Le gain maximum est GMAX = +40dB ; l’amplification maximum est donc
GMAX 40
2pts AMAX 10 20
10 20
100 .
B.III.2. La bande passante correspond à la plage de fréquences pour lesquelles le gain
est supérieur ou égal à GMAX – 3dB ; ici, fC ≈ 1kHz ; la bande passante est donc [0 ;1kHz].
B.III.3. L’amplificateur à le comportement d’un filtre passe bas car le gain est
0,5pt maximum en continu et tend vers -∞ en hautes fréquences.
B.III.4. f = 50Hz, G = OdB ; f = 500Hz, G = -40dB ; l’atténuation est donc de
40dB/décade.
1pt B.III.5. Filtre du second ordre (40 = 2 × 20).
B.III.6. Ce filtre laisse passer la composante continue car son gain est maximal en
continu.
B.III.7. L’harmonique de rang le plus élevé est amplifiée par 100 (de la même façon que
la composante continue) car le gain est toujours de 40dB à 0,085Hz. On peut donc dire
que toutes les composantes harmoniques sont transmises.
B.III.8. Pour i = 12A, uS = ×A×12=0,001×100×12=1,2V.
B.III.9. Voir document réponse 3 :
18pts Partie C
C.I.
C.I.1. ( p) k RTH p ( p) RTH G( p) ; ( p).1 k RTH p RTH G( p) ;
1pt RTH
( p) G ( p) .
.1 k RTH p
1pt C.I.2. T0 = RTH et = k.RTH .
0,113
C.I.3. T0 = RTH = 0,113 et = k.RTH = 35,4 × 0,113 = 4s . D’où ( p) G( p)
.1 4 p
C.II. Réponse indicielle
1pt
531
C.II.1. G ( p)
p
1pt
0,113 531 60
C.II.2. ( p)
.1 4 p p p1 4 p
C.II.3. (t ) 60.1 e
t
2pts 60
C.II.4. lim (t ) lim p. ( p) lim p = 60°C
t p 0 p 0
p1 4 p
C.III.
C.III.1. Système du premier ordre : tangente à l’origine oblique.
C.III.2. 3 = 80°C ; ne correspond pas à l’essai de la question C.II car la température
en régime permanent n’est pas de 60°C.
C.III.3. Pour t = tr5% , = 0,63×60 = 37,8°C ; tr5% ≈ 7,5s.
C.III.4. La courbe qui correspond à l’essai de la question C.II est la courbe 1 car elle
donne = 4s et 1 max = 60°C.
C.III.5. = 60°C ; R () 60C
C.III.6. tr5% = 12s (pour 1 = 0,95 × 60 = 57°C)
26pts Partie D
D.I. Conditions d’acquisition
D.I.1. On a 30 échantillons pour 60s, soit 1 échantillon toutes les deux secondes ;
1 1
1pt fE = 0,5Hz.
TE 2
fE
1pt D.I.2. f max = 0,25Hz.
2
D.I.3. Oui, fE remplit la condition de Shannon car la fréquence maximum à traiter est
fE
inférieure à .
2
1pt D.II. Conversion analogique-numérique
D.II.1. nMAX = 2n – 1 = 28 – 1 = 255
1pt
U PE 4 4
D.II.2. On a q n
8 15,6mV
2 2 256
D.II.3. tC < TE
uS 1
D.II.4. N10 = = 64. N2 = 0100 0000
2pts q 15,625 103
0,5pt
D.III. Traitement numérique
D.III.1. Il s’agit d’un algorithme récursif car la sortie à l’instant n dépend de la
sortie à l’instant (n-1).
D.III.2.
D.III.3. Voir document réponse 4 :
n -1 0 1 2 3 4 5 6 7 8
xn 0 1 0 0 0 0 0 0 0 0
xn-1 0 0 1 0 0 0 0 0 0 0
yn-1 0 0 0 88 88 88 88 88 88 88
yn 0 0 88 88 88 88 88 88 88 88
D.III.4.
D.III.5. Le système numérique est stable car sa réponse impulsionnelle tend vers une valeur
finie.
D.III.6. On a yn 88xn1 yn1 ; la transformation en z donne : Y z 88.z 1. X z z 1.Y z ;
Y z 88.z 1
soit Y z . 1 z 1 88.z 1. X z ;
X z 1 z 1
; en multipliant par z le numérateur et le
Y z 88
dénominateur, on obtient .
X z z 1
X z
64 64 z
D.III.7.
1 z z 1
1
Y z
88 64 z 5632.z
D.III.8. .
z 1 z 1 z 12
D.III.9. Séquence rampe : yn = 5632.n
D.III.10. Energie = puissance × temps ; si la puissance est constante alors l’énergie augmente
linéairement avec le temps.












