BTS IRIS corrigé physique appliquée 2009
DownloadTélécharger
Actions
Vote :
ScreenshotAperçu
Informations
Catégorie :Category: mViewer GX Creator Lua TI-Nspire
Auteur Author: skynet_360rg
Type : Classeur 3.6
Page(s) : 5
Taille Size: 298.73 Ko KB
Mis en ligne Uploaded: 30/03/2015 - 08:49:52
Uploadeur Uploader: skynet_360rg (Profil)
Téléchargements Downloads: 77
Visibilité Visibility: Archive publique
Shortlink : http://ti-pla.net/a179997
Type : Classeur 3.6
Page(s) : 5
Taille Size: 298.73 Ko KB
Mis en ligne Uploaded: 30/03/2015 - 08:49:52
Uploadeur Uploader: skynet_360rg (Profil)
Téléchargements Downloads: 77
Visibilité Visibility: Archive publique
Shortlink : http://ti-pla.net/a179997
Description
BTS IRIS
Session 2009
(Corrigé)
PARTIE A. Moto-réducteur d’entrainement du volet.
T0M
A.1. Le système est du premier ordre : TM(p) est de la forme : .
1 Mp
A.2. τM = 0,1 s.
A.3. tr5% = 3 τM = 0,3 s.
o m
.c
T0M U T0M
A.4. N(p) = TM(p)×U(p) = 0 et lim n(t) = lim p×N(p) = lim U0 = T0M U0
1 Mp p t p p 1 M p
m
lim n(t) = 1,67×6 = 10 tr.s-1
a
t
x
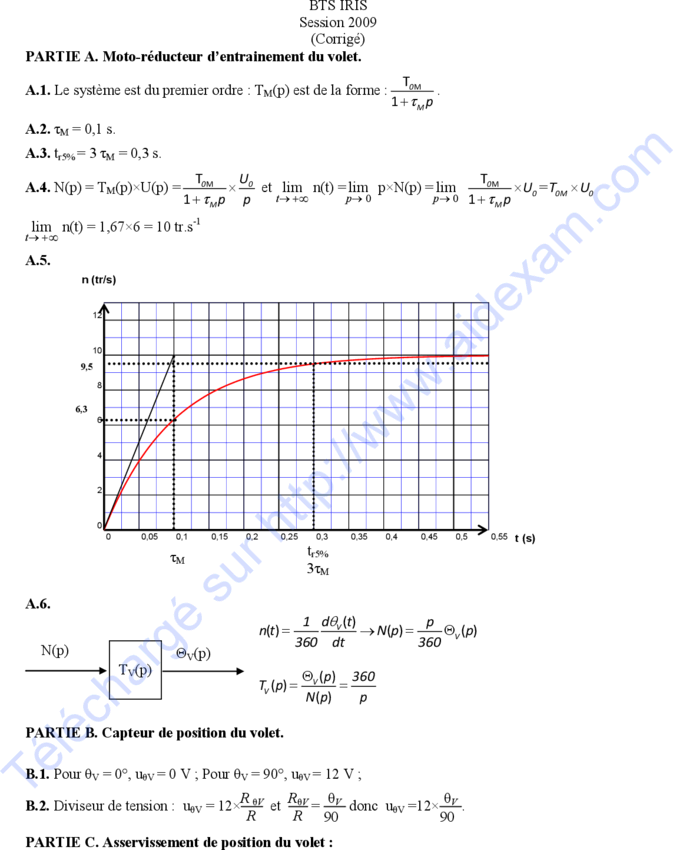
A.5.
e
n (tr/s)
id
12
10
.a
w
9,5
w
8
w
6,3
/
6
:/
4
2
tt p
0
0 0,05 0,1
r
0,15 0,2
h
0,25 0,3 0,35 0,4 0,45 0,5 0,55 t (s)
su
τM tr5%
3τM
é
A.6.
g
1 dV (t) p
r
n(t) N(p) V (p)
360 dt 360
a
N(p) ΘV(p)
h
TV(p) V (p) 360
TV (p)
c
N(p) p
lé
é
PARTIE B. Capteur de position du volet.
T
B.1. Pour θV = 0°, uθV = 0 V ; Pour θV = 90°, uθV = 12 V ;
B.2. Diviseur de tension : uθV = 12×
R θV
R
R
R
θ θ
et θV = V donc uθV =12× V .
PARTIE C. Asservissement de position du volet :
V (p) TV (p) TM (p) C (p) U (p) U v (p) TV (p) TM (p) C (p) U (p) TC (p)V (p)
o m
V (p) TV (p) TM (p) C (p) U (p) TV (p) TM (p) C (p) TC (p) V (p)
.c
m
V (p) 1 TV (p) TM (p) C (p) TC (p) TV (p) TM (p) C (p) U (p)
a
V (p) TV (p) TM (p) C (p)
x
TBF 1 (p)
U (p) 1 TV (p) TM (p) C (p) TC (p)
C.2.
e
id
U (p) TC (p) (p)
.a
(p) TV (p) TM (p) C (p)
TBF 1 (p) V
U (p) 1 TV (p) TM (p) C (p) TC (p)
w
(p) V (p) U (p) T (p) TM (p) C (p) TC (p)
TBF 2 (p) V TBF 1 (p) TC (p) V
w
(p) U (p) (p) 1 TV (p) TM (p) C (p) TC (p)
w
Partie D. Rôle du correcteur.
:/ /
D.1. Le système est du deuxième ordre : dépassement, tangente à l’origine horizontale.
tt p
D.2. L’erreur en régime permanent est nulle car θV = θconsigne
θVmax θV
D.3. D1 = = = 56 %
h
θV
r
D.4. Mφ de l’ordre de 10°
su
g é
a r
c h
lé
T é
D.5. Il faut augmenter la marge de phase pour augmenter la stabilité du système.
D.6.
o m
.c
a m
tr5% = 0,135 s
e x
id
D.7. Le système est du second ordre : la tangente à l’origine est horizontale.
.a
Partie E. Étude du système dans sa version numérique.
w
E.1. Le bloqueur permet de maintenir constante la valeur de l’angle pendant la durée de la conversion
numérique.
E.2. fE = → fE = = 100 Hz.
w
w
TE ×
:/ /
E.3. Le spectre du signal échantillonné boqué peut à cause du repliement se superposer au spectre du
tt p
signal initial.
fE
E.4. On ne devra échantillonner que des fréquences inférieures à = 50 Hz pour respecter la règle de
h
Shannon. Il faut donc couper le domaine Hz ; ∞ .
r
s u
E.5.
S(z) 1, 2 1,1z 1
C (z) S(z) 1 0 , 5z 1 E (z) 1, 2 1,1z 1
é
E (z) 1 0 , 5z 1
g
S(z) 0 , 5z 1S(z) 1, 2E (z) 1,1z 1E (z) S(z) 1, 2E (z) 1,1z 1E (z) 0 , 5z 1S(z)
r
1
Z
sn 1, 2en 1,1en1 0 , 5sn1
E.6.
h a
c
Le système est récursif car l’équation de récurrence fait appel au terme de sortie de rang inférieur à n.
E.7.
lé
é
sn
en
T
1,2
TE TE
-1,1 0,5
E.8.
n 0 1 2 3
en 1 0 0 0
sn 1,2 - 0,5 - 0,25 -0,125
E.9.
{δn} → 1
1, 2 1,1z 1
S(z) C (z) E (z) 1
1 0 , 5z 1
E.10.
lim s n = lim (z-1)E(z) =lim
n∞ z1
1, 2 1,1z 1
z1 1 0 , 5z 1
z 1 = 0
o m
.c
Le correcteur est stable car la réponse impulsionnelle car lim sz n = 0
n∞
m
Partie F. Bus de données.
F.1. tr =
d
v
→ tr = = 50µs.
xa
F.2. Il faut R = RC = 120 Ω.
e
nombre de bits
→ tt = = 154 µs.
id
.a
F.3. Débit =
durée
w
nombre de bits utiles
F.4. Dn = → Dn = 64/154×10-6 = 0,42 Mbit.s-1
durée d'une trame
Partie G. Alimentation en énergie électrique.
w
G.1. = U×I → Pun = 14×90 = 1,26 kW
/ w
:/
Pun P ,
G.2. η = → Pmn = un → Pmn = = 2,0 kW.
tt p
Pmn η ,
Pmn Pmn 2000×60
h
G.3. Pmn = Tm ×Ω → Tm = = → Tm = = 7,64 N.m.
Ω 2πn 2π×2500
r
G.4. U = E - aI ; E = UI=0 =24 V ; Pour I = 20 A, U = 20 V
su
–
→ 20 = 24 – 20a → a = = 0,2 Ω
g é
a r
c h
lé
T é
G.5. U1 = 24 – 0,5I1 → U1 = 24 - 0,2×60 = 12 V
G.6. La tension augmente.
G.7. Iexc doit diminuer.
Partie H. Étude du régulateur.
H.1. U = 14 V
H.2. <uext> uext dt = ×Aire hachurée = ×αT×U = αU
T
o m
.c
T T
H.3. α = 0,75
H.4. Si U diminue il faut que Iext augmente pour compenser la baisse.
H.5. Il faut alors que <uext> augmente donc que α augmente.
a m
e x
id
.a
w
w
/ w
:/
tt p
r h
su
g é
a r
c h
lé
T é
Session 2009
(Corrigé)
PARTIE A. Moto-réducteur d’entrainement du volet.
T0M
A.1. Le système est du premier ordre : TM(p) est de la forme : .
1 Mp
A.2. τM = 0,1 s.
A.3. tr5% = 3 τM = 0,3 s.
o m
.c
T0M U T0M
A.4. N(p) = TM(p)×U(p) = 0 et lim n(t) = lim p×N(p) = lim U0 = T0M U0
1 Mp p t p p 1 M p
m
lim n(t) = 1,67×6 = 10 tr.s-1
a
t
x
A.5.
e
n (tr/s)
id
12
10
.a
w
9,5
w
8
w
6,3
/
6
:/
4
2
tt p
0
0 0,05 0,1
r
0,15 0,2
h
0,25 0,3 0,35 0,4 0,45 0,5 0,55 t (s)
su
τM tr5%
3τM
é
A.6.
g
1 dV (t) p
r
n(t) N(p) V (p)
360 dt 360
a
N(p) ΘV(p)
h
TV(p) V (p) 360
TV (p)
c
N(p) p
lé
é
PARTIE B. Capteur de position du volet.
T
B.1. Pour θV = 0°, uθV = 0 V ; Pour θV = 90°, uθV = 12 V ;
B.2. Diviseur de tension : uθV = 12×
R θV
R
R
R
θ θ
et θV = V donc uθV =12× V .
PARTIE C. Asservissement de position du volet :
V (p) TV (p) TM (p) C (p) U (p) U v (p) TV (p) TM (p) C (p) U (p) TC (p)V (p)
o m
V (p) TV (p) TM (p) C (p) U (p) TV (p) TM (p) C (p) TC (p) V (p)
.c
m
V (p) 1 TV (p) TM (p) C (p) TC (p) TV (p) TM (p) C (p) U (p)
a
V (p) TV (p) TM (p) C (p)
x
TBF 1 (p)
U (p) 1 TV (p) TM (p) C (p) TC (p)
C.2.
e
id
U (p) TC (p) (p)
.a
(p) TV (p) TM (p) C (p)
TBF 1 (p) V
U (p) 1 TV (p) TM (p) C (p) TC (p)
w
(p) V (p) U (p) T (p) TM (p) C (p) TC (p)
TBF 2 (p) V TBF 1 (p) TC (p) V
w
(p) U (p) (p) 1 TV (p) TM (p) C (p) TC (p)
w
Partie D. Rôle du correcteur.
:/ /
D.1. Le système est du deuxième ordre : dépassement, tangente à l’origine horizontale.
tt p
D.2. L’erreur en régime permanent est nulle car θV = θconsigne
θVmax θV
D.3. D1 = = = 56 %
h
θV
r
D.4. Mφ de l’ordre de 10°
su
g é
a r
c h
lé
T é
D.5. Il faut augmenter la marge de phase pour augmenter la stabilité du système.
D.6.
o m
.c
a m
tr5% = 0,135 s
e x
id
D.7. Le système est du second ordre : la tangente à l’origine est horizontale.
.a
Partie E. Étude du système dans sa version numérique.
w
E.1. Le bloqueur permet de maintenir constante la valeur de l’angle pendant la durée de la conversion
numérique.
E.2. fE = → fE = = 100 Hz.
w
w
TE ×
:/ /
E.3. Le spectre du signal échantillonné boqué peut à cause du repliement se superposer au spectre du
tt p
signal initial.
fE
E.4. On ne devra échantillonner que des fréquences inférieures à = 50 Hz pour respecter la règle de
h
Shannon. Il faut donc couper le domaine Hz ; ∞ .
r
s u
E.5.
S(z) 1, 2 1,1z 1
C (z) S(z) 1 0 , 5z 1 E (z) 1, 2 1,1z 1
é
E (z) 1 0 , 5z 1
g
S(z) 0 , 5z 1S(z) 1, 2E (z) 1,1z 1E (z) S(z) 1, 2E (z) 1,1z 1E (z) 0 , 5z 1S(z)
r
1
Z
sn 1, 2en 1,1en1 0 , 5sn1
E.6.
h a
c
Le système est récursif car l’équation de récurrence fait appel au terme de sortie de rang inférieur à n.
E.7.
lé
é
sn
en
T
1,2
TE TE
-1,1 0,5
E.8.
n 0 1 2 3
en 1 0 0 0
sn 1,2 - 0,5 - 0,25 -0,125
E.9.
{δn} → 1
1, 2 1,1z 1
S(z) C (z) E (z) 1
1 0 , 5z 1
E.10.
lim s n = lim (z-1)E(z) =lim
n∞ z1
1, 2 1,1z 1
z1 1 0 , 5z 1
z 1 = 0
o m
.c
Le correcteur est stable car la réponse impulsionnelle car lim sz n = 0
n∞
m
Partie F. Bus de données.
F.1. tr =
d
v
→ tr = = 50µs.
xa
F.2. Il faut R = RC = 120 Ω.
e
nombre de bits
→ tt = = 154 µs.
id
.a
F.3. Débit =
durée
w
nombre de bits utiles
F.4. Dn = → Dn = 64/154×10-6 = 0,42 Mbit.s-1
durée d'une trame
Partie G. Alimentation en énergie électrique.
w
G.1. = U×I → Pun = 14×90 = 1,26 kW
/ w
:/
Pun P ,
G.2. η = → Pmn = un → Pmn = = 2,0 kW.
tt p
Pmn η ,
Pmn Pmn 2000×60
h
G.3. Pmn = Tm ×Ω → Tm = = → Tm = = 7,64 N.m.
Ω 2πn 2π×2500
r
G.4. U = E - aI ; E = UI=0 =24 V ; Pour I = 20 A, U = 20 V
su
–
→ 20 = 24 – 20a → a = = 0,2 Ω
g é
a r
c h
lé
T é
G.5. U1 = 24 – 0,5I1 → U1 = 24 - 0,2×60 = 12 V
G.6. La tension augmente.
G.7. Iexc doit diminuer.
Partie H. Étude du régulateur.
H.1. U = 14 V
H.2. <uext> uext dt = ×Aire hachurée = ×αT×U = αU
T
o m
.c
T T
H.3. α = 0,75
H.4. Si U diminue il faut que Iext augmente pour compenser la baisse.
H.5. Il faut alors que <uext> augmente donc que α augmente.
a m
e x
id
.a
w
w
/ w
:/
tt p
r h
su
g é
a r
c h
lé
T é












