Démonstrations capes - Géométrie
Symétrique par rapport à la première bissectrice

Dans un repère orthonormé (O, i , ⃗j ) (O,
⃗ i , j ), le symétrique du point M(a, b)M(a, b) par rapport à la droite
→ →


y = x y = x est le point M ′ (b, a) M ′ (b, a).

Démonstration

Il suffit de démontrer que la droite y = x y = x
est la médiatrice du segment [M M ′ ] [MM ′ ]
. Les deux droites sont perpendiculaires. En effet, un vecteur directeur de y = x y = x
est u =
⃗ (1, 1)→u = (1, 1)
et un vecteur directeur de (M M ′ ) (MM ′ )
−−−→′ →
est MM = (b − a, a − b) MM ′ = (b − a, a − b)
−−−→′ →
. On vérifie alors facilement que u ⋅⃗ MM = 0 →
u ⋅ MM ′ = 0
.

D'autre part, le milieu de [M M ′ ] [MM ′ ]
est le point I I
de coordonnées ((a + b)/2, (a + b)/2) ((a + b) / 2, (a + b) / 2 )
. Il est bien sur la droite y = x y = x
.


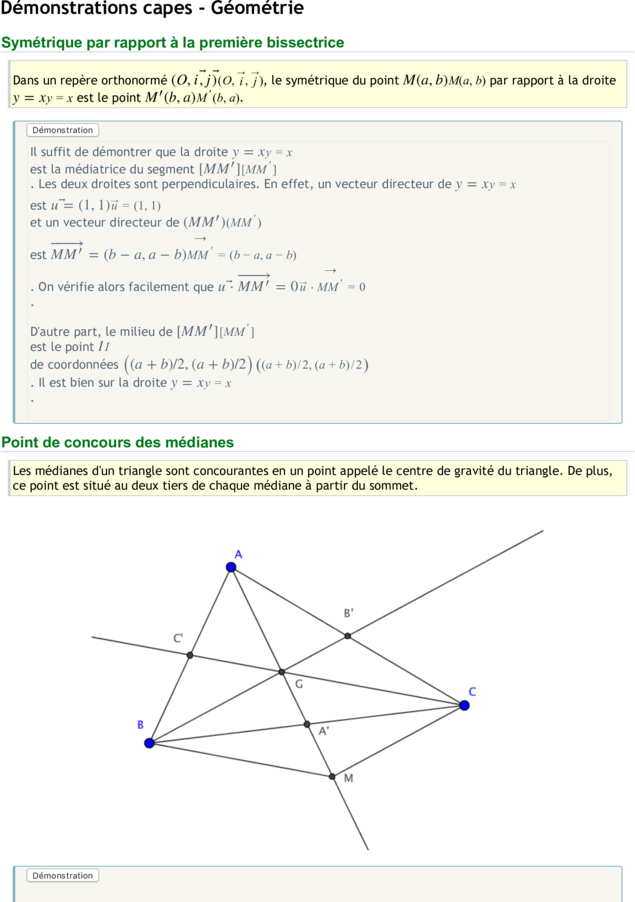
Point de concours des médianes
Les médianes d'un triangle sont concourantes en un point appelé le centre de gravité du triangle. De plus,
ce point est situé au deux tiers de chaque médiane à partir du sommet.




Démonstration
Dans le triangle ABC ABC
, notons A′ A ′
le milieu de [BC][BC]
, B′ B ′
le milieu de [AC][AC]
et C ′ C ′
le milieu de [AB] [AB]
. On note encore GG
le point d'intersection de (BB′ ) (BB ′ )
et de (CC ′ ) (CC ′ )
. et M M
le symétrique de A A
par rapport à GG
. Nous allons prouver que le quadrilatère BMCG BMCG
est un parallélogramme. Pour cela, on remarque que

La droite (BM) (BM) est parallèle à la droite (GC) = (C ′ G) (GC) = (C ′ G). En effet, dans le
triangle ABM ABM, C ′ C ′ est le milieu de [AB] [AB] et GG est le milieu de [AM] [AM]. Le
théorème de la droite des milieux entraîne que (BM) (BM) est parallèle à (C ′ G) (C ′ G).
La droite (CM) (CM) est parallèle à la droite (BG)(BG). Ceci résulte toujours du théorème de la
droite des milieux, mais appliqué cette fois au triangle ACM ACM.

Le quadrilatère BMCG BMCG
est donc un parallélogramme. Ainsi, ses diagonales se coupent en leur milieu, et donc A′ A ′
, le milieu de [BC][BC]
, est aussi le milieu de [MG] [MG]
. En particulier, A′ A ′
est sur la droite (AG) = (MG) (AG) = (MG)
, et donc (AA′ ) (AA ′ )
passe bien par GG
. Enfin, on a

1 1 2
GA′ = GM = AG ⟹ AG = AA′ .
2 2 3
1 1 2
GA ′ = GM = AG ⟹ AG = AA ′ .
2 2 3

On peut aussi démontrer ce théorème sans doute plus facilement avec des vecteurs. En effet,
introduisons le point GG
→
−→
− 2 −−→
→ 2
tel que AG = 3 AA′ AG = AA ′
3
−−→′ −→
− → →′ → →
, c'est-à-dire que 2GA + GA = 0 2GA + GA = 0
. Alors on a aussi
−−→′ 1 −→
− 1 −→
−
GA = GB + GC
2 2
→
′ 1→ 1→
GA = GB + GC
2 2

et donc
−→
− −→
− −→
− →
GB + GC + GA = 0 .
 → → → →
GB + GC + GA = 0.

D'autre part,

−→
− −→
− −−→′
GA + GC = 2GB

→ → →
GA + GC = 2GB ′

et donc

−→
− −−→′ →
GB + 2GB = 0

→ →
→
GB + 2GB ′ = 0

soit encore

−→
− 2 −−→′
BG = BB .
3
→ →
2
BG = BB ′ .
3

Ainsi, GG
est sur la droite (BB′ ) (BB ′ )
. On montre de la même façon que GG
est sur la droite (CC ′ ) (CC ′ )
, et les relations vectorielles donnent en prime la position de GG
sur chaque médiane. Remarquons que les égalités vectorielles que nous avons écrites ne sont rien
d'autre que la traduction de la propriété d'associativité du barycentre.


Point de concours des médiatrices
Dans un triangle ABC, les médiatrices des trois segments [AB] [AB], [BC][BC] et [CA][CA] sont
concourantes.

Démonstration

Rappelons qu'un point M M
est sur la médiatrice de [AB] [AB]
si et seulement si MA = MB MA = MB
. Ainsi, si OO
est le point d'intersection des médiatrices de [AB] [AB]
et de [BC][BC]
, alors on a OA = OBOA = OB
et OB = OCOB = OC
. Ainsi, on a aussi OA = OCOA = OC
et OO
est sur la médiatrice de [AC][AC]
.


Point de concours des hauteurs
Dans un triangle, les trois hauteurs sont concourantes.
Démonstration

Notons ABC ABC
le triangle, (d1)(d1)
la hauteur issue de A A
, (d2)(d2)
la hauteur issue de B B
et (d3)(d3)
la hauteur issue de C C
. On va construire un autre triangle IJK IJK
tel que (d1)(d1)
, (d2)(d2)
et (d3)(d3)
soient les médiatrices des trois côtés de ce triangle, ce qui prouvera le résultat.

Pour cela, on construit

La parallèle à (AB) (AB) passant par C C;
La parallèle à (AC)(AC) passant par B B;
La parallèle à (BC)(BC) passant par A A.

Ces trois droites se coupent en I I
, JJ
et K K
avec A ∈ [JK] A ∈ [JK]
, B ∈ [IK] B ∈ [IK]
et C ∈ [IJ] C ∈ [IJ]
. On va prouver que A A
est le milieu de [JK] [JK]
. Pour cela, remarquons que le quadrilatère AKBC AKBC
est un parallélogramme, puisque les droites (AK) = (JK)(AK) = (JK)
et (BC)(BC)
sont parallèles et que les droites (BK) = (IK) (BK) = (IK)
et (AC)(AC)
sont parallèles. En particulier, on a AK = BC AK = BC
. De la même façon, ABCJ ABCJ
est un parallélogramme, et donc AJ = BC AJ = BC
. Ceci prouve que A A
est le milieu de [JK] [JK]
.

Or, (d1)(d1)
est perpendiculaire à (BC)(BC)
 , donc à (JK) (JK)
et passe par A A
le milieu de [JK] [JK]
. Donc (d1)(d1)
est la médiatrice de [JK] [JK]
. De la même façon, on prouve que (d2)(d2)
est la médiatrice de [IK][IK]
, et que (d3)(d3)
est la médiatrice de [IJ] [IJ]
. Ainsi, (d1)(d1)
, (d2)(d2)
et (d3)(d3)
sont les trois médiatrices du triangle IJK IJK
. Ainsi, elles sont concourantes.


Droite d'Euler
Dans un triangle ABC ABC, notons GG le centre de gravité, H H le point de concours des hauteurs, et OO
le centre du cercle circonscrit. Alors les points G, H, O G, H, O sont alignés. Plus précisément, on a
−→
− −→
− → →
GH = −2GO GH = − 2GO.




Démonstration

Notons A′ A ′
, B′ B ′
et C ′ C ′
les milieux respectifs des segments [BC][BC]
, [CA][CA]
et [AB] [AB]
, et hh
l'homothétie de centre GG
et de rapport −2 − 2
 −−→′ → →
−→
−
. Alors, d'après le théorème concernant le centre de gravité, on sait que GA = −2GA GA = − 2GA ′
. Ainsi, h(A′ ) = Ah(A ′ ) = A
. De la même façon, h(B′ ) = Bh(B ′ ) = B
et h(C ′ ) = C h(C ′ ) = C
.

En particulier, on a h(A′ B′ ) = (AB) h(A ′ B ′ ) = (AB)
et h(C ′ ) = C h(C ′ ) = C
. Considérons maintenant la médiatrice de [AB] [AB]
, c'est-à-dire la droite passant par C ′ C ′
et perpendiculaire à [AB] [AB]
. C'est aussi la droite passant par C ′ C ′
et perpendiculaire à (A′ B′ ) (A ′ B ′ )
, puisque (AB) (AB)
est parallèle à (A′ B′ ) (A ′ B ′ )
par le théorème de la droite des milieux. Une homothétie conservant l'orthogonalité, l'image par hh
de cette médiatrice est la droite perpendiculaire à h(A′ B′ ) = (AB) h(A ′ B ′ ) = (AB)
et passant par h(C ′ ) = C h(C ′ ) = C
, c'est-à-dire la hauteur issue de C C
...