Attention : Ce code ne fonctionne pas si votre numworks tourne avec une version 1.2 ou supérieure. Un script est présenté plus tard sur ce topic pour les version 1.2 ou supérieure.
- Code: Select all
import kandinsky
N_iteration = 40
X_min = -2
X_max = 2
Y_min = -2
Y_max = 2
for x in range(320):
for y in range(240):
c_r = -1
c_i = 0.3
z_r = X_min +(X_max-X_min)*x/320
z_i = Y_min +(Y_max-Y_min)*y/240
i=0
while (i < N_iteration ) and ((z_r*z_r)+(z_i*z_i) < 4):
i+1=i
stock = z_r
z_r = z_r * z_r - z_i * z_i + c_r
z_i = 2 * stock * z-i + c_i
rgb = int(255*i/N_iteration)
col = kandinsky.color(rgb,rgb,rgb)
kandinsky.set_pixel(x,y,col)
ça affiche ça

Alors oui, le programme est très proche du programme fourni avec la version bêta du python, mais j'y ai mis 4 variables permettant de modifier les parties du plan affichées par la calculatrice (et de faire des zooms)
exemple avec c_r et c_i = 0.36 :

c'est pas mal, mais en modifiant un peu le plan :
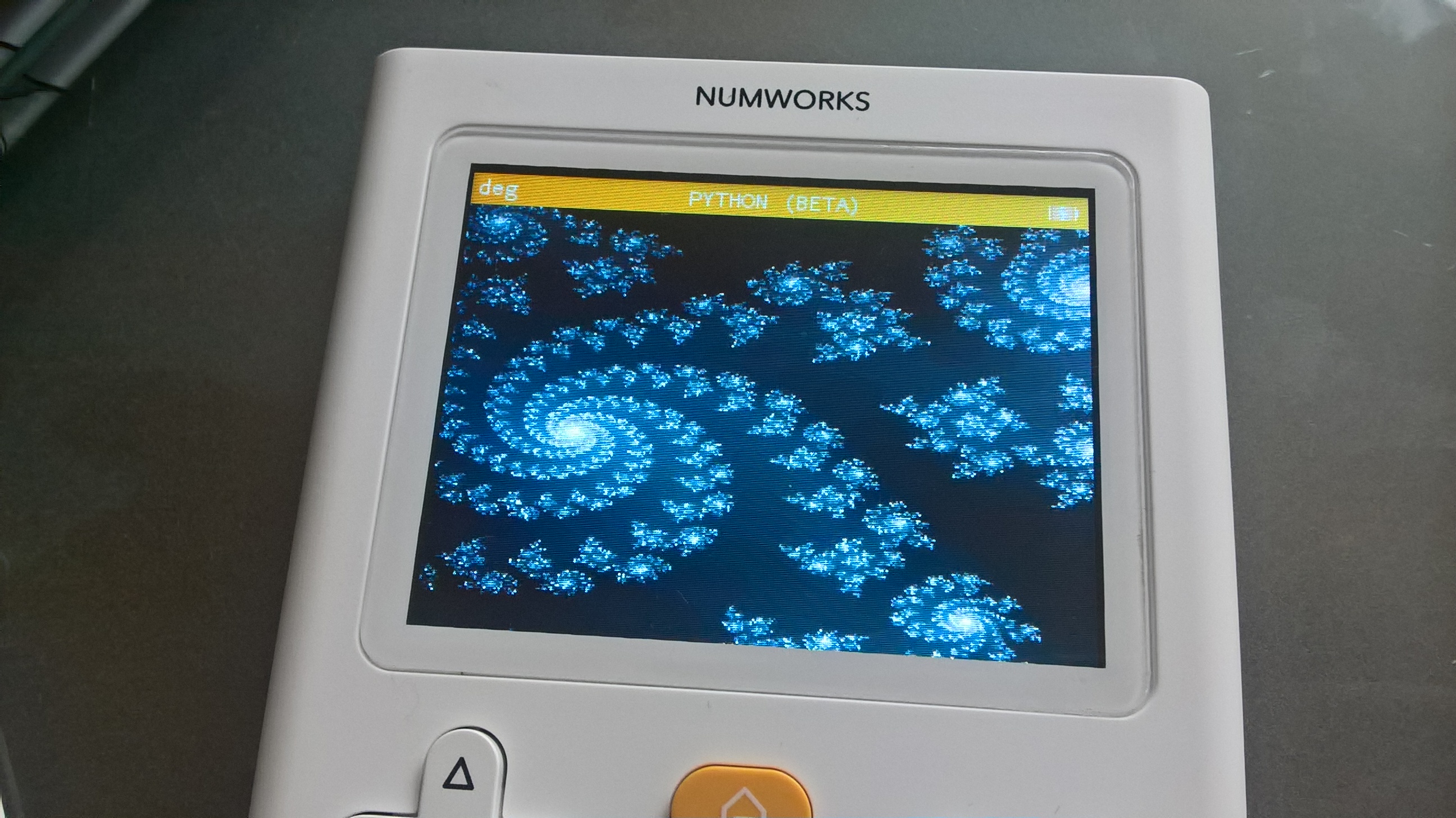
ça donne d'un coup plus envie
 (pensez à augmenter le nombre d'itérations)
(pensez à augmenter le nombre d'itérations)c'est pratique quand la fractale générée n'est pas connexe
Pour modifier les couleurs, il suffit de modifier la 20ème ligne de code (pensez à rajouter int( entre chaque "rgb" car chaque valeur se doit d'être entière
pour c_r = 0.3 et c_i = 0.5 :

c_r = 0.285 et c_i = 0.013 avec recadrage

amusez vous bien




























