CPLua - What is wrong with this while loop?

[MrMagoo]

Bonjour! J'espère que vous allez tous bien.
Je suis brésilien et je ne parle pas Français. Je m'excuse et si vous me le permettez, j'écrirai en Anglais dans ce post.

Also, sorry for my bad English too - I'm a Portugues native speaker.

I hope that this forum is active, in order to us talk about this issue.

I have a few calculators and sometimes I like to make some benchmark tests with them. Maybe the "Calculator Olympic Games", if you wish.
I use to figure tests that everyone can play.
But, this time, I tried something different and excluded the non-programable calculators.
My intentions were to analyze the native programming language and also a similar algorithm to them, in order to compare their performance (maybe it is interesting to post the results and the codes in another post).
Well, we all know that the Classpad does not have a native good programming environment when you have performance in mind (even more when you are dealing with numerical analys with a lot of loops). In this way, myself and all the other calculators agreed that we will allow CP330 to use CPLua in substitution of natural Casio Basic.
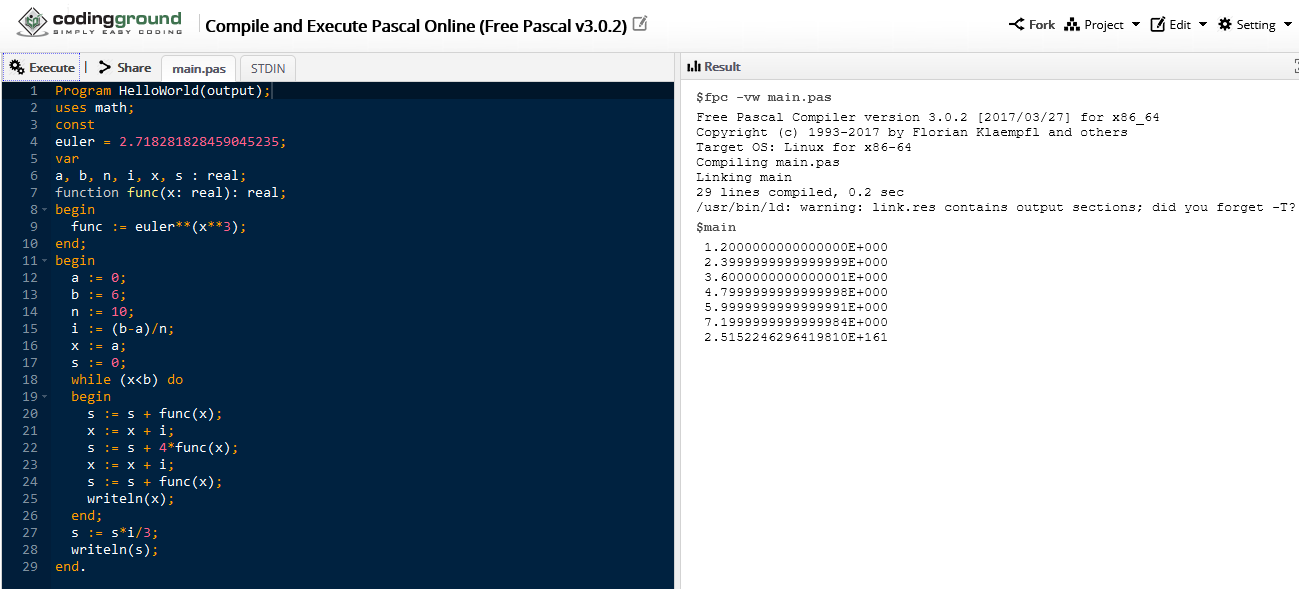
The benchmark used is to perform Simpson Rule as presented in this link for the Ti-81 (https://www.ticalc.org/pub/81/basic/math/simpson.81) PS: on line 5, the correct code is a capital i instead of one. The corrected instruction is : (B - A) / N -> I
The code was minor adjusted according the possible commands on each calculator.

So, they all have to perform the following definite integral:

e^(x^3), from 0 to 6, with n=1000

It was based on the test presented here: https://www.youtube.com/watch?v=DHRsvSTGiBc

The CPLua code used is:

Code: Select all

--start
function y(x)
  return math.exp(x^3)
end

n = 1000
a = 0 + 0.
b = 6 + 0.
i = (b-a)/n
x = a + 0.
s = 0.0
while ( x < b ) do
  s = s+y(x)
  x = x+i
  s = 4*y(x)+s
  x = x+i
  s = s+y(x)
end
s = s*i/3
print(s)

Ok. All the calculators performed well and provided the same answer (obviously, with their respective performance time).
But CPLua in Classpad did not.
CPLua ignores when x = 6, when it should stop. It iterates one more time, as if the instruction were ( x <= b ) .

I tried everything that I figured that it could be and did not find anything. I tried CPLua 0.8 and 0.10a.

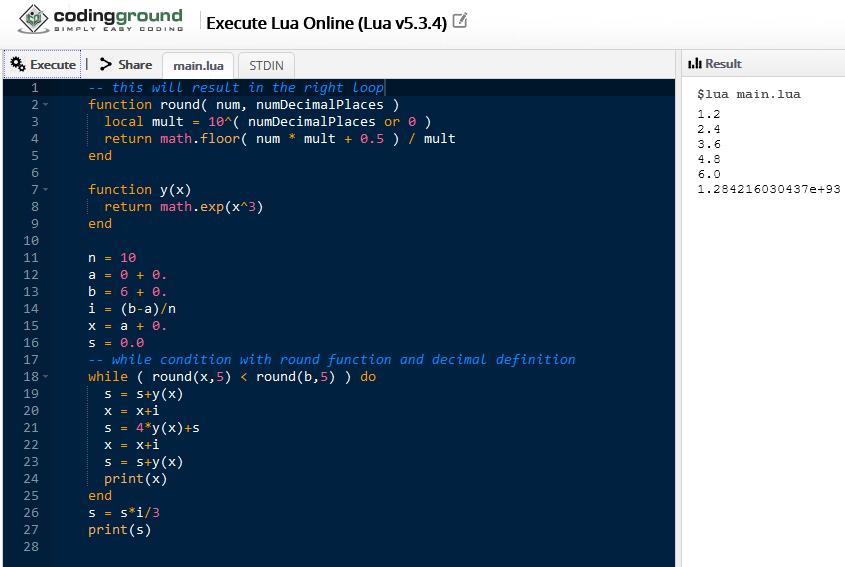
So, I changed the code, reduced the d to 10 and requested an x print before the while end. Just to investigate, the code became:

Code: Select all

n = 10
a = 0 + 0.
b = 6 + 0.
i = (b-a)/n
x = a + 0.
s = 0.0
while ( x < b ) do
  s = s+y(x)
  x = x+i
  s = 4*y(x)+s
  x = x+i
  s = s+y(x)
  print(x)
end
s = s*i/3
print(s)

The output is:
1.2
2.4
3.6
4.8
6
7.2
2.51522462964201e+161
Done.

The 7.2 there is totaly wrong. It is not suposed to be there.
If I change b=5, so it works. If I change b to 6.000001 it works
But if I change b=6.00001 it does not work!!!!


Going a little bit further.
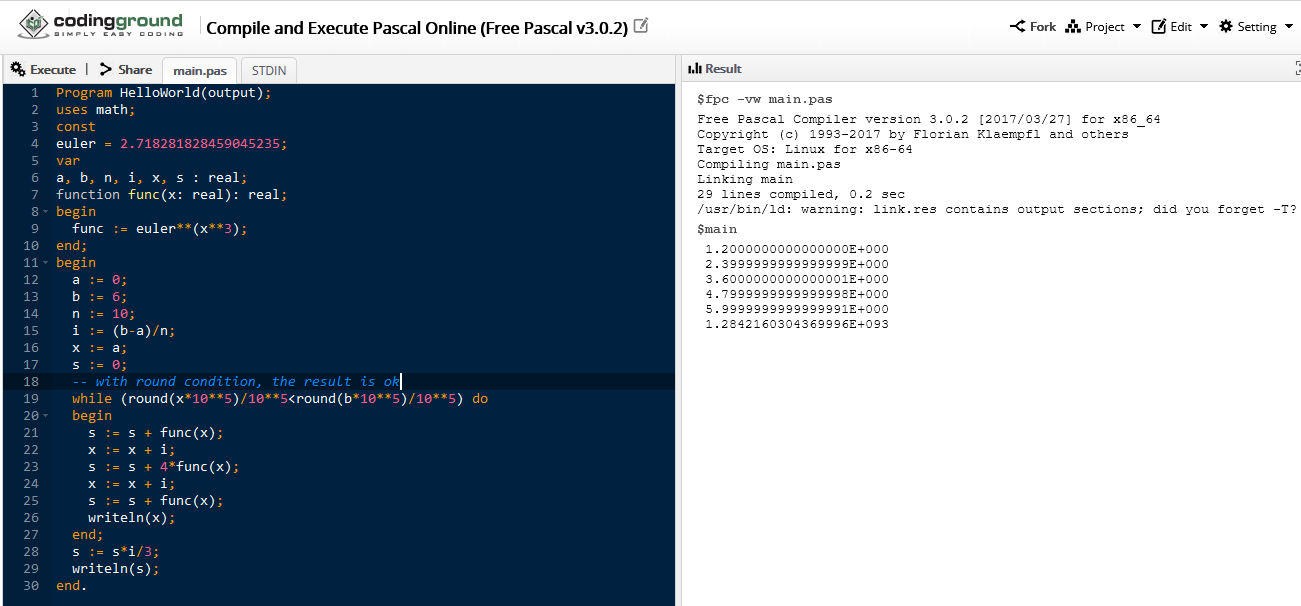
I implemented a function to round the x and the b value in the while condition. The function is (found somewhere, but I forgot to get the link):

Code: Select all

function round( num, numDecimalPlaces )
  local mult = 10^( numDecimalPlaces or 0 )
  return math.floor( num * mult + 0.5 ) / mult
end

And the while condition became:

Code: Select all

while ( round( x ) < round ( b ) ) do

The complete code is:

Code: Select all

function round( num, numDecimalPlaces )
  local mult = 10^( numDecimalPlaces or 0 )
  return math.floor( num * mult + 0.5 ) / mult
end

function y(x)
  return math.exp(x^3)
end

n = 10
a = 0 + 0.
b = 6 + 0.
i = (b-a)/n
x = a + 0.
s = 0.0
while ( round( x ) < round ( b ) ) do
  s = s+y(x)
  x = x+i
  s = 4*y(x)+s
  x = x+i
  s = s+y(x)
  print(x)
end
s = s*i/3
print(s)


It solved the problem but increased 25% in processing time .

In another forum, I started the same discussion. Piu58 send some thoughts that I was think about also - maybe a base 10 to base 2 convertion could be the problem. The post is here https://community.casiocalc.org/topic/8069-cplua-what-is-wrong-with-this-while-loop/#entry63773

Taking this road, when a = 0, b = 6, n = 10, the value of i became i = 0.6

0.6 to base 2 is --> 0.6 (base10) = 0.10011001100110011001100110011... (base2) (it is recurring, as a repeating decimal, or in this way, a repeating binary? sorry for the bad english)

When we truncate the binary to the digits presented above and get back to base 10, we get:

0.10011001100110011001100110011 (base2) = 0.59999999962747097015 (base10)

For sure, anything that tries to represent 0.6 in binary and is truncated, will be lower than 0.6.

If we accumulate x with this i lower than 0.6 for 10 times, x will be something lower than 6.

buuuuuuut, when I asked to print (x), the CPLua presents x = 6 (in this way 10 times 0.6 - see the output presented in the begining of this post) and, in this way, it is representing x as 6 in base 10.
I am assuming that when I asked for x, CP330 and CPLua recognized x as 6, and give back to me a '6', so it printed x=6. I was expecting the same behavior in the while condition.

The algorithm in CP330 Casio Basic performs slowly (n = 100 it halts), but make the things right, and stops when x=6. Just in CPLua I got the problem.

So why did CPLua do not stop when x was 6? Does anybody knows why it is happening with CPLua?
Also, does anybody have any suggestion to how to solve it without the round() function in CPLua?

[Adriweb]

Hmm.

FYI, the output with LuaJIT is:

1.2
2.4
3.6
4.8
6

and

1.284216030437e+93

[MrMagoo]

AdriWeb, thanks for your reply and to test it on LuaJIT.
Your answer is correct for n=10. It is the same as we get in all other calculators using the programmed method.

All my Tis, HPs and Other Casios did it well too (even my brave fx-700p from the early 80s did it... the beauty take its 8 minutes to peforme the n=1000, but make it wonderfully).

Only ClassPad 330 with CPLua that presented the issue.
It happened with CPLua 0.8 and CPLua 0.10a

It is not necessary to say, but be aware that n=10 is to few divisions to provide a good result to this definite integral.

The correct answer is expected to be something like ≈ 5.963938092×10^91

As you increase the n the better is the results but also increase the processing time (obviously).
I used 10 just to investigate the while loop.

I don't know why it is happening on CPLua. This is the first time that I get something like this.

I searched for the developers activities, but it seems that they are doing other stuff nowadays.
As long as I was able to find, the last developers were Cartix and Binary_man from Planète Casio. Their last login were on 2019 and 2018, respectively.
It is hard to find some active foruns nowadays.

Going further, I inserted the code in tutorialsponint (https://www.tutorialspoint.com/execute_lua_online.php) and removed the round() function from the while condition. The results were the same as in CPLua. See the following picture:



PS: its better to set some decimal cases to the round function. I forgot to do that in the previous example. The following picutre is better example for the use of the programmed CPLua round function.
If I insert the round() function in the while loop, it gets the right answer. See the following



HP-39gII did not presented the problem, but the good old Pascal (online) also presented the same issue. See the following:



The same pascal code, with the round condition:



So the LuaJIT is performing well even without the round() function in the while condition?

[rentech7289]

The 7.2 there is totaly wrong. It is not suposed to be there.
If I change b=5, so it works. If I change b to 6.000001 it works
But if I change b=6.00001 it does not work!!!!

The problem comes from conversion of a decimal number into binary. Moreover, more zeros you have in your number (between decimal point and last digit), more your test will fail. The fact is intern results aren't always exact. An approximative result can't be compared to an exact value with a defined margin of error. The problem is to fixed this one without an alteration of the behavior of the concerned algorithm.
To understand this problem, the mathematical relation with logarithms have a similar behavior. You can replace

$mathjax$a * b$mathjax$

by

$mathjax$c^d$mathjax$

, with

$mathjax$d=(log_c(a) + log_c(b))$mathjax$

and where

$mathjax$c$mathjax$

is the logarithmic base. But the precision of the result will follow the algorithmic precision. Some algorithms converts directly in binary, others use a mantissa with an exposant (but mantissa is/can be directly converted in binary). A few algorithms converts decimal numbers into integers with exponent, for example BigDecimal class in Java. This last ways is the better for non irrational numbers. But with irrational numbers, you find again the same problem: a calculation precision...
I'm not a Casio specialist, but your problem seems to be due to the software, not to the algorithm.

[Witairsturs1963]

I'd really like to help, but I don't fully understand this topic myself. Somehow, training is not easy for me, and I already doubt that I can become a good specialist. I spend a lot of time on this, sometimes using https://plainmath.net/post-secondary to find answers to these and similar math problems. I am interested in this topic and I am sure that I will soon be able to improve this knowledge, but for this, I will definitely have to make a lot of effort.

[toml_12953]

Bonjour! J'espère que vous allez tous bien.
I have a few calculators and sometimes I like to make some benchmark tests with them. Maybe the "Calculator Olympic Games", if you wish.
I use to figure tests that everyone can play.
But, this time, I tried something different and excluded the non-programable calculators.
My intentions were to analyze the native programming language and also a similar algorithm to them, in order to compare their performance (maybe it is interesting to post the results and the codes in another post).
Well, we all know that the Classpad does not have a native good programming environment when you have performance in mind (even more when you are dealing with numerical analys with a lot of loops). In this way, myself and all the other calculators agreed that we will allow CP330 to use CPLua in substitution of natural Casio Basic.
The benchmark used is to perform Simpson Rule as presented in this link for the Ti-81 (https://www.ticalc.org/pub/81/basic/math/simpson.81) PS: on line 5, the correct code is a capital i instead of one. The corrected instruction is : (B - A) / N -> I
The code was minor adjusted according the possible commands on each calculator.

I tried it on Python:

Code: Select all

from math import *
def y(x):
  return exp(x**3)

n = 10
a = 0 + 0.
b = 6 + 0.
i = (b-a)/n
x = a + 0.
s = 0.0

while ( x < b ):
   s = s+y(x)
   x = x+i
   s = 4*y(x)+s
   x = x+i
   s = s+y(x)
   print(x)
s = s*i/3
print(s)

and got:

1.2
2.4
3.6
4.8
5.999999999999999
7.199999999999998
2.5152246296420105e+161

In Decimal BASIC

Code: Select all

FUNCTION y(x)
   LET y=EXP(x^3)
END FUNCTION

LET n = 10
LET a = 0 + 0.
LET b = 6 + 0.
LET i = (b-a)/n
LET x = a + 0.
LET s = 0.0

DO WHILE ( x < b )
   LET s = s+y(x)
   LET x = x+i
   LET s = 4*y(x)+s
   LET x = x+i
   LET s = s+y(x)
   PRINT x
LOOP
LET s = s*i/3
PRINT s
END


I got:

1.2
2.4
3.6
4.8
6
1.28421603043712E+93

[Bisam]

Everything was already told previously but here is my word.

A float number is ALWAYS an approximation of a real number.
Furthermore, the IEEE standard defining how float numbers should be stored and used let developpers do it in several ways.
Hence, in some languages, the behavior is different than in others... but it can be worse : the same language can produce different results when executed on different machines, or even in different environments on the same machine !

Here, the difference comes from the diffrent ways of storing the number

$mathjax$0.6$mathjax$

and the different ways in adding it multiple times.

But the error would not appear using a 'for' loop instead of a 'while'... and since we know from the beginning the number of loops to be done, a 'for' loop should be preferred !

[parisse]

Everything was already told previously but here is my word.

A float number is ALWAYS an approximation of a real number.

This is not quite correct. You can use floats to store exact data and some libraries do that (for fast modular computations). More precisely, the C double type can store exactly integers that are smaller (in absolute value) than 2^53. And also some rationals (the denominator must be a power of 2 for base 2 floats, or a divisor of a power of 10 for base 10 floats, and numerator/denominator must not be too large). 0.6 can not be represented exactly by a base 2 float type, but it can using a base 10 float type.