Expliquer que 1+1=2 et passer pour un mathématicien
Posted: 24 Nov 2011, 16:39Salut, je sais pas si ce que je poste est déjà connu ou pas, mais voilà qui va plaire aux nuls en maths qui veulent avoir l'air de posséder le niveau bac !
Il est en fait facile de démontrer que pour tout x :
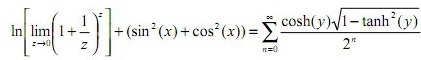
Vous êtes d'accord, n'est-ce pas ? c'est simplissime...
Je vous montre comment: il suffit de savoir que 1+1=2, et deux trois autres petites formules pour remplacer les 1 et les 2...
_________________________________________________________________________
- Premièrement, on sait qu'en maths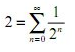
Je crois que ça s'appelle le paradoxe de Zénon, mais je ne suis pas sur...
_________________________________________________________________________
ensuite, on sait qu'en trigo sin²(x)+cos²(x)=1 ...
__________________________________________________________________________
On sait également, presque par définition du logarithme népérien, que ln(e)=1 , et que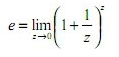
attention, mon image est fausse, c'est bien la limite mais quand z tend vers +infini et non pas 0...
_________________________________________________________________________
On prend donc 1+1=2,
et on remplace donc nos 1 et notre 2 par chaque formule respective
:
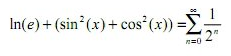
puis on remplace notre e par sa formule que j'ai déjà donnée ci dessus, mais que je redis: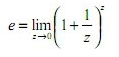
_________________________________________________________________________
On sait ensuite que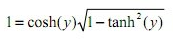
pour ceux qui on fait de la trigo... un peu plus poussée 
et donc on remplace le 1 du "1/(2^n)" par cette notation plus... tordue.
_________________________________________________________________________
on a donc bien la formule:
.
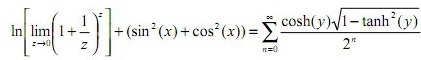
Plus exactement, si vous voulez démontrer que cette formule est toujours vraie et passer pour un pro, il faudra faire ce que je viens de dire, mais dans l'autre sens...
Vous aboutirez ainsi sur 1+1=2, ce qui, je pense, suffira à prouver à votre entourage que vous avez raison et que vous êtes un brillant mathématicien.
enjoy !
Il est en fait facile de démontrer que pour tout x :
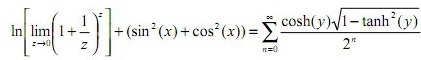
Vous êtes d'accord, n'est-ce pas ? c'est simplissime...
Je vous montre comment: il suffit de savoir que 1+1=2, et deux trois autres petites formules pour remplacer les 1 et les 2...
_________________________________________________________________________
- Premièrement, on sait qu'en maths
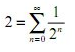
Je crois que ça s'appelle le paradoxe de Zénon, mais je ne suis pas sur...
_________________________________________________________________________
ensuite, on sait qu'en trigo sin²(x)+cos²(x)=1 ...
__________________________________________________________________________
On sait également, presque par définition du logarithme népérien, que ln(e)=1 , et que
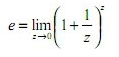
attention, mon image est fausse, c'est bien la limite mais quand z tend vers +infini et non pas 0...
_________________________________________________________________________
On prend donc 1+1=2,
et on remplace donc nos 1 et notre 2 par chaque formule respective
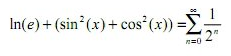
:puis on remplace notre e par sa formule que j'ai déjà donnée ci dessus, mais que je redis:
_________________________________________________________________________
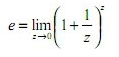
On sait ensuite que
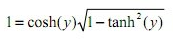pour ceux qui on fait de la trigo... un peu plus poussée et donc on remplace le 1 du "1/(2^n)" par cette notation plus... tordue.
_________________________________________________________________________
on a donc bien la formule:
.
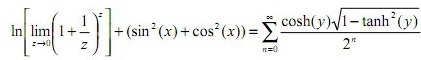
Plus exactement, si vous voulez démontrer que cette formule est toujours vraie et passer pour un pro, il faudra faire ce que je viens de dire, mais dans l'autre sens...
Vous aboutirez ainsi sur 1+1=2, ce qui, je pense, suffira à prouver à votre entourage que vous avez raison et que vous êtes un brillant mathématicien.
enjoy !
