Bonne fête de π et calcul de ses 996 premières décimales !
Posted: 15 Mar 2016, 00:04Aujourd'hui 14 mars débute la semaine des mathématiques.
Attardons-nous un petit peu sur cette date qui nous donne en écriture numérique 14/03.
Au format de date américain cela nous donne 3/14, soit les premiers chiffres de π.
Et oui, nous sommes la journée de π et nous vous souhaitons donc une bonne fête de π.
C'est d'ailleurs une journée exceptionnelle, puisque l'écriture étendue 3/14/16 nous donne exceptionnellement cette année un arrondi à 5 chiffres correct du nombre π !
Notre calculatrice TI-83 Premium CE nous donne une écriture décimale du nombre π à 10 chiffres : 3.141592654.
En fait, notre machine calcule sur des nombres à 14 chiffres et se contente d'afficher au maximum les 10 chiffres les plus significatifs.
Il nous suffit d'annuler les chiffres les plus significatifs pour obtenir ce que la calculatrice nous cache : pour elle, π est en réalité le nombre décimal à 14 chiffres 3.1415926535898.
En réalité π n'est pas un nombre décimal. C'est-à-dire qu'il est impossible de l'écrire de façon exacte en écriture décimale, une telle écriture nécessitant une infinité de chiffres après la virgule.
Et si nous essayions donc d'obtenir à la calculatrice une meilleure approximation de π ?
Plusieurs algorithmes ou formules de calcul existent. Nous allons opter ce soir pour la formule de Machin datant de 1706 qui offre un bon compromis entre nombre d'opérations et convergence :
Faut-il encore développer un programme qui soit capable d'effectuer ces opérations sur des nombres à plus de 14 chiffres.
On peut par exemple représenter de tels nombres par des listes de chiffres, les listes pouvant avoir jusqu'à 999 éléments sur notre calculatrice.
Reste alors encore à programmer les différentes opérations chiffre à chiffre comme au primaire (ici l'addition, la soustraction, la multiplication, la division et l'arctangente), et c'est chose faite ci-contre avec notre nouveau programme ExtraPi !
Les derniers chiffres n'étant pas fiables selon une telle méthode, au final ExtraPi te permettra en théorie d'afficher jusqu'à 997 chiffres pour le nombre π !
Nombre d'astuces seraient envisageables pour désintégrer cette limite.
En pratique, la TI-83 Premium CE arrive à te sortir les 20 premiers chiffres en une 30aine de secondes, mais en fait la progression n'est pas proportionnelle loin de là.
Le programme ExtraPi a une particularité originale : malgré l'usage de l'écran graphique c'est exactement le même code qui permet d'afficher aussi bien sur les anciens écrans monochromes 96x64 pixels que les nouveaux écrans couleur 320x240 pixels. 
Il suffit pour cela de calculer les dimensions en pixels de l'écran utilisable avec par exemple
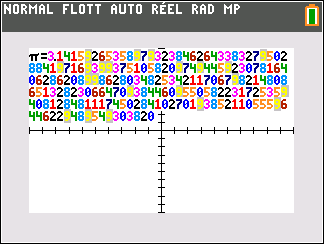
En pratique sur la TI-83 Premium CE j'ai souhaité attribuer une couleur différente à chaque chiffre pour donner une idée de la répartition de ceux-ci, et j'ai donc dû quand même fournir deux versions du sous-programme d'affichage, car les anciens modèles monochromes refusent bêtement la réception de tout programme contenant des instructions couleur (ce qui est d'autant plus regrettable que j'avais pris la peine de mettre des instructions conditionnelles pour ne pas exécuter les instructions couleur sur les modèles monochromes).
Ci-dessus tu as donc une écriture décimale couleur à 200 chiffres du nombre π. Auras-tu le courage d'aller plus loin avec ta calculatrice TI-83 Premium CE ?
Téléchargement : https://tiplanet.org/forum/archives_voir.php?id=457080
Attardons-nous un petit peu sur cette date qui nous donne en écriture numérique 14/03.
Au format de date américain cela nous donne 3/14, soit les premiers chiffres de π.
Et oui, nous sommes la journée de π et nous vous souhaitons donc une bonne fête de π.
C'est d'ailleurs une journée exceptionnelle, puisque l'écriture étendue 3/14/16 nous donne exceptionnellement cette année un arrondi à 5 chiffres correct du nombre π !
Notre calculatrice TI-83 Premium CE nous donne une écriture décimale du nombre π à 10 chiffres : 3.141592654.En fait, notre machine calcule sur des nombres à 14 chiffres et se contente d'afficher au maximum les 10 chiffres les plus significatifs.
Il nous suffit d'annuler les chiffres les plus significatifs pour obtenir ce que la calculatrice nous cache : pour elle, π est en réalité le nombre décimal à 14 chiffres 3.1415926535898.
En réalité π n'est pas un nombre décimal. C'est-à-dire qu'il est impossible de l'écrire de façon exacte en écriture décimale, une telle écriture nécessitant une infinité de chiffres après la virgule.
Et si nous essayions donc d'obtenir à la calculatrice une meilleure approximation de π ?
Plusieurs algorithmes ou formules de calcul existent. Nous allons opter ce soir pour la formule de Machin datant de 1706 qui offre un bon compromis entre nombre d'opérations et convergence :
$mathjax$\pi=4\left(4arctan \frac{1}{5}-arctan\frac{1}{239}\right)$mathjax$
On peut par exemple représenter de tels nombres par des listes de chiffres, les listes pouvant avoir jusqu'à 999 éléments sur notre calculatrice.
Reste alors encore à programmer les différentes opérations chiffre à chiffre comme au primaire (ici l'addition, la soustraction, la multiplication, la division et l'arctangente), et c'est chose faite ci-contre avec notre nouveau programme ExtraPi !
Les derniers chiffres n'étant pas fiables selon une telle méthode, au final ExtraPi te permettra en théorie d'afficher jusqu'à 997 chiffres pour le nombre π !
Nombre d'astuces seraient envisageables pour désintégrer cette limite.
En pratique, la TI-83 Premium CE arrive à te sortir les 20 premiers chiffres en une 30aine de secondes, mais en fait la progression n'est pas proportionnelle loin de là.
Le programme ExtraPi a une particularité originale : malgré l'usage de l'écran graphique c'est exactement le même code qui permet d'afficher aussi bien sur les anciens écrans monochromes 96x64 pixels que les nouveaux écrans couleur 320x240 pixels. Il suffit pour cela de calculer les dimensions en pixels de l'écran utilisable avec par exemple
1+arrondir((Xmax-Xmin)/ΔX,0) ou 1+arrondir((Xmax-Xmin)/PasX,0) selon les modèles et d'en tenir compte. En pratique sur la TI-83 Premium CE j'ai souhaité attribuer une couleur différente à chaque chiffre pour donner une idée de la répartition de ceux-ci, et j'ai donc dû quand même fournir deux versions du sous-programme d'affichage, car les anciens modèles monochromes refusent bêtement la réception de tout programme contenant des instructions couleur (ce qui est d'autant plus regrettable que j'avais pris la peine de mettre des instructions conditionnelles pour ne pas exécuter les instructions couleur sur les modèles monochromes).
Ci-dessus tu as donc une écriture décimale couleur à 200 chiffres du nombre π. Auras-tu le courage d'aller plus loin avec ta calculatrice TI-83 Premium CE ?
Téléchargement : https://tiplanet.org/forum/archives_voir.php?id=457080
