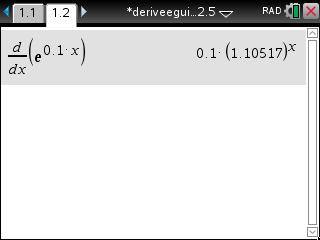
Dérive les fonctions de façon fiable sur TI-Nspire non-CAS !
 As-tu acheté ta calculatrice TI-Nspire CX neuve ou quasi neuve pour moins de 100€ sur Internet en pensant faire une excellente affaire ?
As-tu acheté ta calculatrice TI-Nspire CX neuve ou quasi neuve pour moins de 100€ sur Internet en pensant faire une excellente affaire ?Si oui une fois reçue tu te rends compte que tu t'es bien fait(e) avoir... car il y a deux modèles aux noms similaires et que nous n'avons pas du tout classés de la même façon pour la rentrée 2015 :
- TI-Nspire CX
- TI-Nspire CX CAS
En gros la TI-Nspire CX a des capacités mathématiques pas plus évoluées que celles d'une TI-82/83/84 Plus, et même inférieures à celles de la TI-83 Premium CE.

Ce n'est pas pour rien que la TI-Nspire CX n'est pas distribuée en boutique traditionnelle en France et ne se trouve que via Internet, en importation pour les modèles neufs.
Mais bref, le mal est fait. Que faire maintenant ?
Il était auparavant possible d'installer le système TI-Nspire CX CAS sur sa calculatrice TI-Nspire CX avec l'outil nLaunchy, mais il nécessite la version 3.1 du Boot2 qui ne fonctionnera pas correctement avec les calculatrices produites à partir de mars 2013 suite à l'introduction de la révision matérielle J.

Pire, tenter la manipulation jusqu'au bout avec une calculatrice récente reviendra à détruire la machine, la laissant coincée dans un état inutilisable sans possibilité de réparation logicielle.


 Une autre solution était de programmer un moteur de calcul formel, ce qui avait été réalisé avec la bibliothèque Alg.
Une autre solution était de programmer un moteur de calcul formel, ce qui avait été réalisé avec la bibliothèque Alg.Hélas, le projet avait été très rapidement abandonné par son auteur, dans un état où bien des résultats fournis étaient faux.

Nous avions certes pris la peine de le mettre à jour le programme et d'en améliorer significativement la fiabilité, mais il n'empêche qu'il n'était selon nous pas assez fiable pour une utilisation en examen.


 Aujourd'hui dans ce contexte, c'est un nouveau projet compatible TI-Nspire CX non-CAS qui voit le jour, nDerive.
Aujourd'hui dans ce contexte, c'est un nouveau projet compatible TI-Nspire CX non-CAS qui voit le jour, nDerive. 
Il est certes bien moins ambitieux. Ce n'est pas un moteur de calcul formel complet puisqu'il ne sait faire qu'une seule chose, calculer des dérivées, et qu'il ne sera même pas capable de simplifier le résultat.
Mais à la différence, tirant les leçons de l'échec de la bibliothèque Alg, nous avons fait un gros effort au niveau de la fiabilité de l'outil.
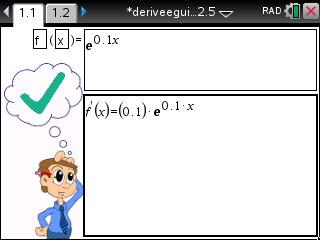
En effet, pour la toute première fois sur TI-Nspire, le programme dispose d'un assistant virtuel intégré qui te dira si le résultat qu'il a trouvé est juste, faux, ou bien si il ne sait pas !

Notons que la capture fausse ci-dessus a été prise avec une ancienne version (il n'y a plus d'erreur connue à ce jour), d'où la sortie de l'outil.

Mais si tant est que des erreurs soient encore possibles, contrairement aux outils précédents il te sera donc indiqué clairement de ne pas recopier bêtement !

 nDerive a été conçu pour couvrir l'ensemble du programme du lycée et des premières années d'études supérieures, jusque dans les exercices les plus complexes et pas seulement en mathématiques !
nDerive a été conçu pour couvrir l'ensemble du programme du lycée et des premières années d'études supérieures, jusque dans les exercices les plus complexes et pas seulement en mathématiques !Il est par exemple capable de te dériver des fonctions à paramètres, un exploit sur calculatrice non-CAS !

Attention toutefois à ne pas oublier de préciser les symboles de multiplications implicites entre les variables. Pour la calculatrice,
ax ce n'est pas pareil que a∙x. 
En conséquence, nDerive ne te servira pas seulement à répondre bêtement à des questions de dérivation, mais sera également capable de te rappeler des formules de dérivées usuelles du cours de Mathématiques à des fins de justification ou dans le contexte de questions de Restitution Organisée de Connaissances (ROC), ainsi que des formules de Physique-Chimie !

 Mais ce n'est pas tout ! Le programme est même capable de dériver des expressions utilisant d'autres fonctions !
Mais ce n'est pas tout ! Le programme est même capable de dériver des expressions utilisant d'autres fonctions ! 
En conséquence de façon similaire, le programme sera capable de te rappeler les formules de dérivation d'opérations du cours !

Le coeur du programme avec le moteur de dérivation en langage Basic est l'oeuvre de Hamza.S.
Un grand merci à toi de notre part à tous. Non seulement tu es déjà disponible quasiment 24h/24 pour aider et dépanner les utilisateurs sur le chat, mais en prime tu trouves le temps de faire encore plus en créant ce qui est de loin l'outil de dérivation le plus génial jamais sorti pour TI-Nspire CX sans avoir besoin d'installer Ndless !

Pour ma part, j'ai codé l'interface Lua permettant la saisie et l'affichage des fonctions et résultats en écriture naturelle, ainsi que l'assistant virtuel d'auto-vérification des résultats.
Fais-en bon usage, et n'hésite pas à nous signaler toute erreur de calcul - ce qui nous permettra d'améliorer et parfaire encore l'outil d'ici les examens du mois de juin.

Attention toutefois. Si vous passez un examen qui interdit les fonctionnalité CAS à travers une liste de modèles autorisés ne mentionnant que la TI-Nspire CX et pas la TI-Nspire CX CAS, comme c'est le cas au Portugal et aux Pays-Bas par exemple, il est probable que l'usage de cet outil soit considéré comme de la fraude.

Concernant la France, si tu passes ton examen à compter de 2018, pas le choix il va te falloir racheter une calculatrice. Car le mode examen rendra ce programme inutilisable.

Téléchargement : https://tiplanet.org/forum/archives_voir.php?id=534590