Forum TI-Planet.org

...et pas forcément très lié aux graphes non plus en fait. C'est juste la sortie que je veux sous forme de graphe mais le problème est peut être tout autre.

Bref, quel est le problème ? Imaginez un plan 2D avec des points qu'on appelera "nœuds" dessus. Le problème est de trouver les nœuds voisins (notion que j'invente pour le problème, pas forcément une notion mathématique existante) de chaque nœud.
Et qu'est-ce qu'un nœud voisin ? La définition "mathématique" que j'ai trouvée est la suivante :
Deux nœuds X et Y sont voisins s'il existe un chemin entre X et Y tel que pour tout point p sur ce chemin, le nœud le plus proche de p est soit X soit Y.

Et des exemples :

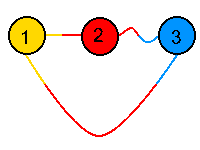
Vous avez trois nœuds ici, alignés, avec des chemins dessinés entre les deux. Vous constatez qu'il existe bien un chemin entre 1 et 2 qui valide la propriété précédente, idem pour 2 et 3 (même si un chemin droit marchait aussi, celui-ci fonctionne tout autant), mais pas entre 1 et 3 puisque vous aurez toujours un point sur le chemin qui vous rendra plus proche de 2 que de 1 et 3.


Et dans le cas d'un "triangle" en revanche, ça fonctionne, tous les nœuds sont voisins deux à deux (aucun chemin n'a été dessiné entre 1 et 2 ni entre 2 et 3 mais vous pouvez les trouver sans moi...).


Et du coup la question... Comment je code ça ?
Alors notez que je ne demande pas directement un code C/C++ fonctionnel, mais si vous trouvez des définitions équivalentes à celle-là mais avec une traduction algorithmique plus évidente, ça m'aiderait déjà beaucoup. Parce que tester tous les chemins possibles entre deux nœuds sur un plan (un ensemble plutôt grand déjà...) puis tous les points dessus (même remarque...), ça ne risque pas d'être très rapide.

Je ne suis pas sûr que ça marche, mais mon idée serait la suivante.

Pour chaque paire de noeuds distincts, tu traces un trait entre les deux et puis tu gardes en mémoire l'équation de la médiatrice.
Tu remarques que ça te permet de créer plusieurs zones dans le plan, et pour chaque noeud la zone associée est l'ensemble des points du plan dont le noeud le plus proche est celui qu'on vient de choisir. A chaque noeud tu peux associer un polygone qui vient d'être tracé (tu calcules les points d'intersection des différentes droites pour déterminer les points qui définissent ces polygones).

Ainsi, pour deux noeuds distincts X, et Y, X et Y sont reliés si et seulement si les deux polygones associés ont au moins un point en commun. Tout chemin dont tous les points sont dans l'un ou l'autre des polygones fait alors l'affaire.

Si N est le nombre de noeuds, on aurait une complexité en O(N²).

Après, il y a une imprécision : quand tu dis "pour tout point p sur ce chemin, le nœud le plus proche de p est soit X soit Y", est-ce que c'est le plus proche au sens strict ou au sens large du terme ?

Par exemple, si t'as des noeuds aux coordonnées (-2,0), (2,0), (0,2), (0,-2), avec ce que j'ai dit il y a un chemin entre les deux premiers, à savoir celui à vol d'oiseau. Mais au point (0,0), t'es à équidistance des quatre noeuds...

Voilà, j'espère ne pas avoir écrit de connerie.

C'est pas des conneries en général
Et ça s'approche de ça qui a un rapport avec ça qui semble correspondre à mon problème... mais en 2D majoritairement, alors que mon vrai problème est en 3D, j'ai juste fait des dessins et explications en 2D pour simplifier.

Le problème, c'est la définition des zones. Puisque pour chaque couple de nœuds, on a la médiatrice, mais ensuite il faut déterminer quelles médiatrices se coupent où pour trouver les zones. Chose très simple à faire à la main sur un dessin, mais demander à un algorithme de le faire est une autre histoire... surtout en 3D -.-

noelnadal wrote:Après, il y a une imprécision : quand tu dis "pour tout point p sur ce chemin, le nœud le plus proche de p est soit X soit Y", est-ce que c'est le plus proche au sens strict ou au sens large du terme ?

Par exemple, si t'as des noeuds aux coordonnées (-2,0), (2,0), (0,2), (0,-2), avec ce que j'ai dit il y a un chemin entre les deux premiers, à savoir celui à vol d'oiseau. Mais au point (0,0), t'es à équidistance des quatre noeuds...

Comme les physiciens diraient, y'a aucun cas réel où le seul chemin qui pourrait valider la propriété poserait un problème d'équidistance
Mais bon, on va dire que si ça arrive, on prend la définition large et on valide.

Il me semble qu'il s'agit de la triangulation de De Launay de ton nuage de points. C'est le graphe dual du diagramme de Voronoi que tu peux calculer en avec l'algorithme de Fortune, mais il y a aussi aussi moyen de la calculer directement en aussi
Tu as alors la propriété que deux points sont "liés au sens d'Hayleia" si et seulement si ils sont reliés par une arête dans la triangulation de De Launay du nuage de points

C'est les liens que j'ai donnés dans mon post juste au dessus Delaunay et Voronoï
Le problème majeur étant qu'ils sont en 2D, donc juste pour l'algo en n², le coup du "le triangle contenant s", ça me marche pas. Et je ne sais pas si remplacer partout "triangle" par "tétraèdre" ça marche, et comment.

Bon au pire, je fais une grosse approximation où je prends les X plus proches, mais c'est un peu ridicule...

Ah, en 3D c'est possible aussi, après je ne te garantis rien pour ce qui est de la complexité...
Tu as sûrement déjà cherché mais au cas où : developpez
Sinon : rapide et encore plus rapide
Je n'ai pas exactement regardé ce que renvoient les algos mais normalement, une fois que tu as la triangulation de De Launay tu devrais pouvoir faire tes tests en