Correction algorithme Concours Général Mathématiques 2013

[critor]

Oui, j'ai vu cette bizarrerie sur le graphique après avoir mis ton algorithme.
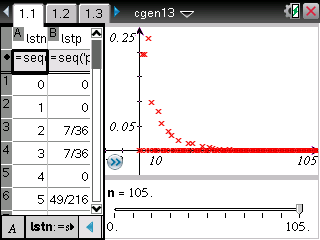
Le point d'abscisse 7 est positionné plus bas alors que les points suivants semblent avoir la même position.
Cela casse notamment la décroissance conjecturée à partir du rang 5.


Ok, donc on obtient:
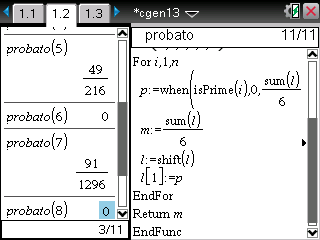
P(X=7)=127/1296 avec l'algorithme récursif
P(X=7)=91/1296 avec l'algorithme itératif

Donc en gros dans certains cas, soit le récursif compte des choses en double, soit l'itératif oublie de compter des choses...

7 doit correspondre à un cas particulier que l'un des deux algorithmes gère mal.
Resterait à comprendre lequel et pourquoi.

[critor]

J'ai étudié le cas X=7 à la main.

Les chemins possibles sont:

• 0 1 4 6 7 (p=1/1296)
• 0 1 4 7 (p=1/216)
• 0 1 7 (p=1/36)
• 0 1 6 7 (p=1/216)
• 0 6 7 (p=1/36)
• 0 4 6 7 (p=1/216)
• 0 4 7 (p=1/36)

Par somme, j'obtiens 127/1296.

Donc sauf erreur de raisonnement, il semble que l'algorithme itératif oublie quelque chose dans le cas particulier n=7.


C'est un cas absolument passionnant et étrange, puisque les algorithmes sont d'accord avant et après pour les résultats que l'on a!

[Bisam]

J'ai trouvé : mon algorithme renvoie la moyenne des valeurs de l APRES avoir modifié l... et dans certains cas, il oublie donc une valeur.
Il suffit d'enregistrer la bonne valeur avant de modifier la liste pour que ça fonctionne.

Je te laisse modifier, critor, je n'arrive pas à faire le copier-coller correctement sur cette fichue tablette.

[critor]

Merci beaucoup pour ton travail sur ce problème!

[critor]

Voici les captures d'écran de la version itérative de l'algorithme et ses résultats:




La version itérative est beaucoup plus performante, et moyennant quelques secondes sur TI-Nspire, on atteint bien le cas P(X=105) cette fois-ci.

Voici le document TI-Nspire associé:
archives_voir.php?id=13545

[Bisam]

En fait, on pouvait même conserver le même nombre de variables en changeant l'ordre des affectations.

Code: Select all

Define probato(n)=
Func
Local i,l,p
If not isprime(n)
  Return 0
l:={1,0,0,0,0,0}
For i,1,n
  p:=sum(l)/6
  l:=shift(l)
  l[1]:=when(isprime(i),0,p)
EndFor
Return p
EndFunc

La raison pour laquelle la méthode est bien plus rapide est que l'algorithme est linéaire, autrement dit, le nombre d'opérations effectuées est (grosso modo) proportionnel à n.
Dans l'algorithme récursif, le nombre d'opérations était bien plus élevé et dans le pire des cas proportionnel à n^n car on recalculait plusieurs fois les mêmes probabilités intermédiaires.