Correction 1er algorithme BAC ES-L 2013
Dans la news précédente, nous te faisions remarquer que le tout premier sujet de maths du BAC ES-L 2013 pour les candidats du lycée français d'Inde à Pondichéry était tombé avec un algorithme.
Le voici:

Question 3)c)
Cet algorithme implémente une suite U définie par:
Il s'agit en fait de la suite C définie dans le contexte de l'exercice.
La suite étant ici géométrique de premier terme strictement positif et de raison 1,025 strictement supérieure à 1, c'est une suite strictement croissante.
La boucle 'tant que' incrémente l'indice n en partant de 0 et s'arrête lorsque l'on réalise le contraire de U≤S, c'est-à-dire U>S.
En sortie de la boucle, l'indice n correspond donc au premier terme de la suite ayant dépassé la valeur S saisie.
Le but de l'algorithme est donc de retourner la 1ère année où la somme placée aura strictement dépassé la valeur S saisie.
Question 3)b)
Si ce qui précède a été anticipé, il est facile d'obtenir la valeur retournée en demandant un simple tableau de valeurs de la suite C de l'exercice, et en rajoutant 2000 à la valeur d'indice n trouvée.
Sinon, il suffit de traduire l'algorithme en un programme sur sa calculatrice et de le lancer.
Le voici par exemple pour toutes les calculatrices graphiques TI-73 à TI-84:
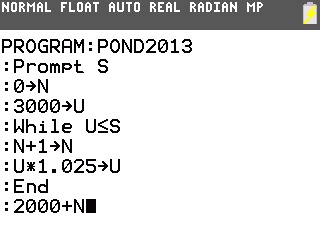

La réponse est donc 2004.
Question 3)a)
On nous demande ici de réaliser une sorte de trace de l'algorithme, avec les états des variables N, U et du test U≤S à chaque étape de l'algorithme.
Il est ultra facile de l'obtenir en rajoutant un simple affichage en début de boucle!
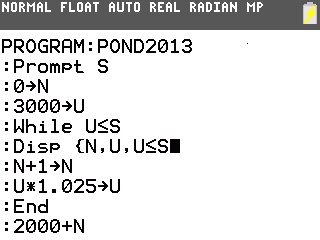

Notons que la calculatrice affiche ici pour le test 1 pour vrai et 0 pour faux.
Mais petit problème, nous n'obtenons pas ici l'état final avec le test faux, puisque dans ce cas on ne passe pas dans la boucle.
Pas de problème, il suffit de rajouter un affichage après la fin de boucle!
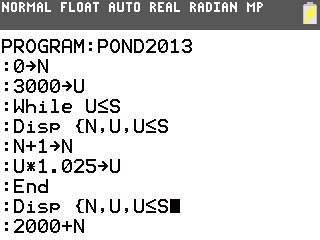
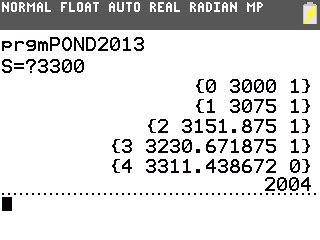
Et voilà, le tableau prêt à être recopié!
La même chose est bien évidemment réalisable sur TI-Nspire:
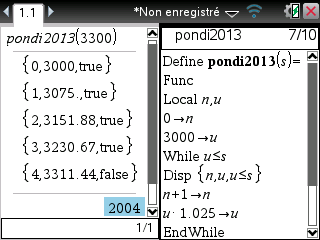
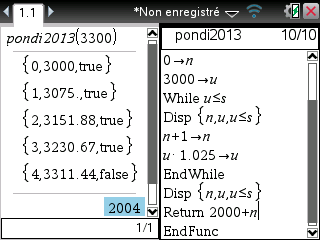
Ou encore sur Casio Graph:


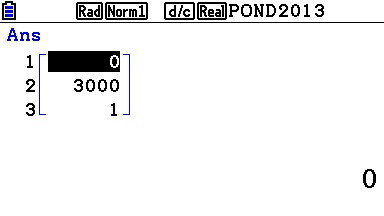
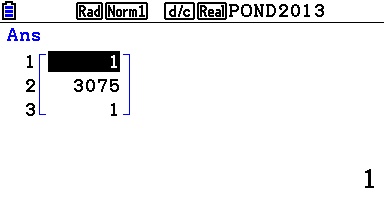
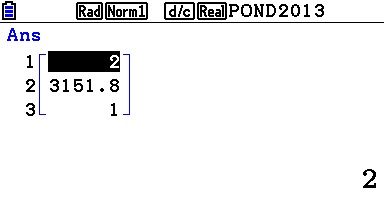
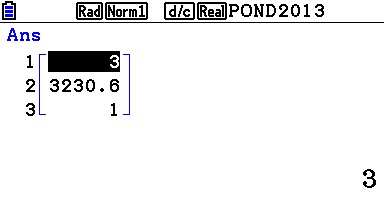
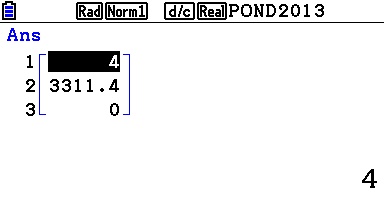

Lien:
BAC ES 2013 - Maths Obligatoire (Inde - avril 2013)
Le voici:

Question 3)c)
Cet algorithme implémente une suite U définie par:
- U0=3000
- Un+1=Un*1,025 (augmentation de 2,5%)
Il s'agit en fait de la suite C définie dans le contexte de l'exercice.
La suite étant ici géométrique de premier terme strictement positif et de raison 1,025 strictement supérieure à 1, c'est une suite strictement croissante.
La boucle 'tant que' incrémente l'indice n en partant de 0 et s'arrête lorsque l'on réalise le contraire de U≤S, c'est-à-dire U>S.
En sortie de la boucle, l'indice n correspond donc au premier terme de la suite ayant dépassé la valeur S saisie.
Le but de l'algorithme est donc de retourner la 1ère année où la somme placée aura strictement dépassé la valeur S saisie.
Question 3)b)
Si ce qui précède a été anticipé, il est facile d'obtenir la valeur retournée en demandant un simple tableau de valeurs de la suite C de l'exercice, et en rajoutant 2000 à la valeur d'indice n trouvée.
Sinon, il suffit de traduire l'algorithme en un programme sur sa calculatrice et de le lancer.
Le voici par exemple pour toutes les calculatrices graphiques TI-73 à TI-84:


La réponse est donc 2004.
Question 3)a)
On nous demande ici de réaliser une sorte de trace de l'algorithme, avec les états des variables N, U et du test U≤S à chaque étape de l'algorithme.
Il est ultra facile de l'obtenir en rajoutant un simple affichage en début de boucle!



Notons que la calculatrice affiche ici pour le test 1 pour vrai et 0 pour faux.
Mais petit problème, nous n'obtenons pas ici l'état final avec le test faux, puisque dans ce cas on ne passe pas dans la boucle.
Pas de problème, il suffit de rajouter un affichage après la fin de boucle!



Et voilà, le tableau prêt à être recopié!

La même chose est bien évidemment réalisable sur TI-Nspire:


Ou encore sur Casio Graph:








A bientôt! 

Lien:
BAC ES 2013 - Maths Obligatoire (Inde - avril 2013)