Correction algorithme BAC L 2012 Nouvelle Calédonie
Bonjour à tous!
Aujourd'hui nous allons nous intéresser à l'algorithme qui est tombé en novembre 2012 au BAC L de Nouvelle Calédonie, et ce n'est pas pour ça qu'il en est moins intéressant, au contraire!

Bon avant d'aller plus loin, il se trouve que cet algorithme est manifestement faux puisque la boucle 'Tant que' n'est pas fermée.
Si on le traduit tel quel sur calculatrice, les comportements seront très variés. Selon les modèles nous pourrons obtenir une erreur ou un comportement différent de celui attendu.
Je vous propose donc la correction suivante:

Question 1:
On nous demande donc dès le départ de donner les sorties de l'algorithme lorsque B=2 et N=12.
Le plus simple est donc de traduire cet algorithme en un programme pour nos calculatrices graphiques.
Le voici pour calculatrice graphique TI-73 à TI-84:

Ou le voici encore pour calculatrice Casio Graph:
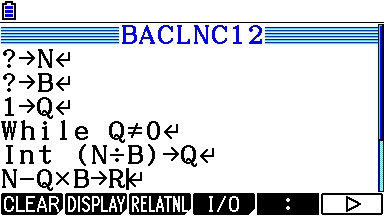
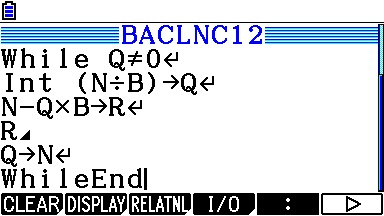
Nous obtenons les sorties suivantes:

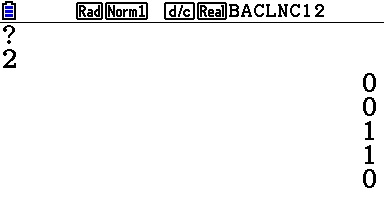
Notre TI-84 Plus C Silver Edition affiche ici 0011 et notre Casio Prizm fx-CG20 00110.
Sur Casio Prizm, le dernier 0 n'est pas un affichage correspond en fait au résultat de la dernière instruction, l'affectation de la variable N avec la valeur 0 de Q. Il remplace en fait le "Done" de la TI-84.
Bref, il ne compte pas et la sortie est donc bien 0011 dans les deux cas.
La même chose est réalisable sur TI-Nspire:
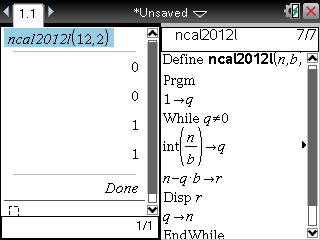
Question 2a:
On nous demande maintenant de recommencer avec B=3 et n=346.
Voici:
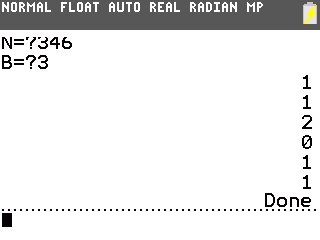
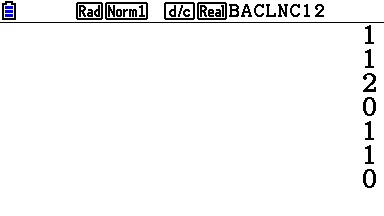
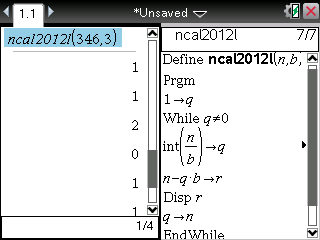
La réponse est donc 112011.
Question 2b:
Comme par hasard, on nous demande maintenant l'écriture de 346 en base 3, mêmes données donc que la question précédente.
Il se trouve que c'est 110211, et l'on peut remarquer que c'est donc l'envers de notre réponse à la question précédente.
Question 3:
L'exemple de la question précédente nous permet de répondre ici: le rôle de l'algorithme est de donner, de droite à gauche, l'écriture du nombre N en base B.
Lien:
Annales des sujets inédits du BAC L 2013
Aujourd'hui nous allons nous intéresser à l'algorithme qui est tombé en novembre 2012 au BAC L de Nouvelle Calédonie, et ce n'est pas pour ça qu'il en est moins intéressant, au contraire!


Bon avant d'aller plus loin, il se trouve que cet algorithme est manifestement faux puisque la boucle 'Tant que' n'est pas fermée.
Si on le traduit tel quel sur calculatrice, les comportements seront très variés. Selon les modèles nous pourrons obtenir une erreur ou un comportement différent de celui attendu.
Je vous propose donc la correction suivante:

Question 1:
On nous demande donc dès le départ de donner les sorties de l'algorithme lorsque B=2 et N=12.
Le plus simple est donc de traduire cet algorithme en un programme pour nos calculatrices graphiques.
Le voici pour calculatrice graphique TI-73 à TI-84:

Ou le voici encore pour calculatrice Casio Graph:


Nous obtenons les sorties suivantes:


Notre TI-84 Plus C Silver Edition affiche ici 0011 et notre Casio Prizm fx-CG20 00110.
Sur Casio Prizm, le dernier 0 n'est pas un affichage correspond en fait au résultat de la dernière instruction, l'affectation de la variable N avec la valeur 0 de Q. Il remplace en fait le "Done" de la TI-84.
Bref, il ne compte pas et la sortie est donc bien 0011 dans les deux cas.
La même chose est réalisable sur TI-Nspire:

Question 2a:
On nous demande maintenant de recommencer avec B=3 et n=346.
Voici:



La réponse est donc 112011.
Question 2b:
Comme par hasard, on nous demande maintenant l'écriture de 346 en base 3, mêmes données donc que la question précédente.
Il se trouve que c'est 110211, et l'on peut remarquer que c'est donc l'envers de notre réponse à la question précédente.
Question 3:
L'exemple de la question précédente nous permet de répondre ici: le rôle de l'algorithme est de donner, de droite à gauche, l'écriture du nombre N en base B.
A bientôt!
Lien:
Annales des sujets inédits du BAC L 2013