Correction algorithme BAC L France septembre 2012
Et nous revoici pour décortiquer devant vous un nouvel algorithme du BAC, cette fois-ci celui tombé au BAC L 2012 en France à la session de remplacement de septembre 2012.

Là encore, la fin de boucle tant que est omise, mais la différence est que l'on a l'indentation qui ne permet donc aucune ambiguïté.
Question 1a:
On nous demande donc l'affichage de l'algorithme pour différentes valeurs de l'entrée A.
Il nous suffit de le traduire en un programme de quelques lignes pour nos calculatrices graphiques et nous aurons la réponse sans effort!
Le voici par exemple pour calculatrices graphiques TI-73 à TI-84:
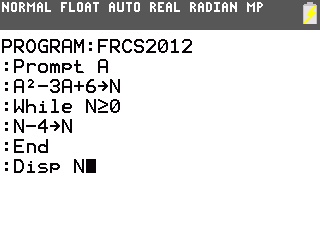
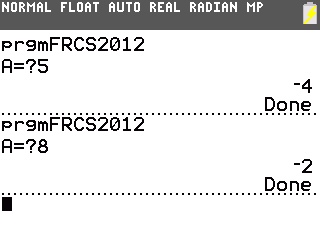
Et suivent donc les réponses pour A=5, A=8 et A=9, qui sont respectivement -4, -2 et -4.

Question 1b:
Il nous faudrait donc maintenant modifier l'algorithme pour qu'il affiche le reste de la division euclidienne de A²-3A+6 par 4, deux nombres effectivement utilisés par l'algorithme.
Il serait déjà utile de connaître les valeurs du nombre A²-3A+6 afin d'en déduire le reste attendu, et également ce qui ne va pas dans l'algorithme actuel.
Commençons donc par modifier le programme afin d'afficher le nombre A²-3A+6:
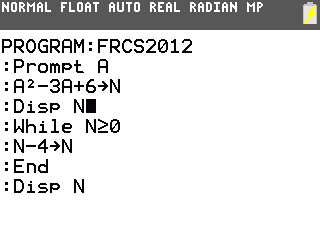
Voyons donc maintenant ce que nous obtenons:
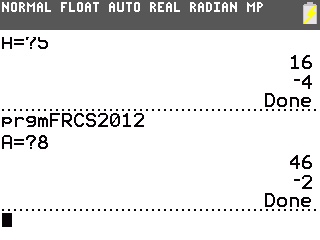
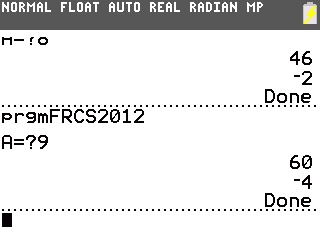
Pour A=5, A²-3A+6=16 et le nombre affiché est -4.
Pour A=8, A²-3A+6=46 et le nombre affiché est -2.
Pour A=9, A²-3A+6=60 et le nombre affiché est -4.
On remarque que le nombre N affiché est toujours strictement négatif, ce qui est normal puisque la boucle TantQue se termine sur la condition N<0.
Or, un reste de division euclidienne par 4 est par définition un nombre entier compris entre 0 et 3.
Il y a ici une itération de trop dans la boucle qui soustrait 4, ce qui rend le résultat négatif.
Deux solutions sont envisageables pour corriger cela.
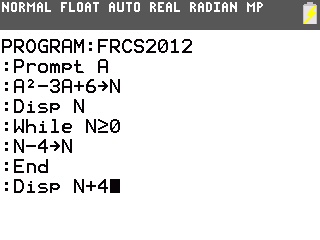
On peut par exemple tout simplement annuler l'itération supplémentaire en ajoutant 4 au résultat:
Afficher la valeur de N+4
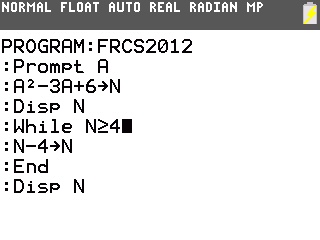
On bien, on change le test de la boucle afin qu'elle se termine une itération plus tôt, ce qui est une meilleure solution algorithmique puisqu'on évite des calculs inutiles à la machine:
Tant que N≥4
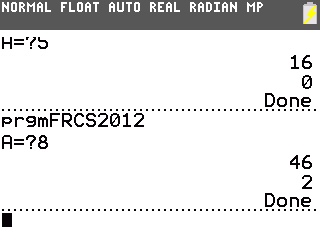
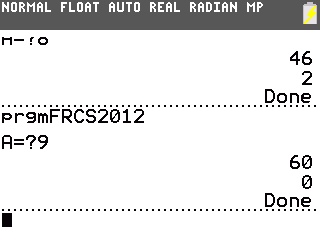
Dans les deux cas, on obtient désormais les restes attendus, respectivement 0, 2 et 0:
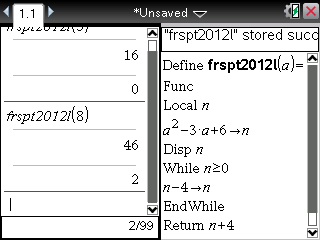
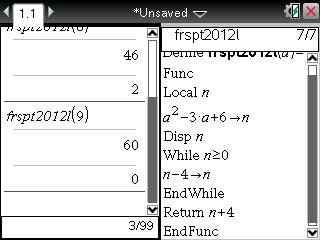
La même chose est bien évidemment réalisable sur TI-Nspire:
... ou encore sur Casio Graph:




Lien:
BAC L 2013: annales des sujets inédits

Là encore, la fin de boucle tant que est omise, mais la différence est que l'on a l'indentation qui ne permet donc aucune ambiguïté.

Question 1a:
On nous demande donc l'affichage de l'algorithme pour différentes valeurs de l'entrée A.
Il nous suffit de le traduire en un programme de quelques lignes pour nos calculatrices graphiques et nous aurons la réponse sans effort!

Le voici par exemple pour calculatrices graphiques TI-73 à TI-84:

Et suivent donc les réponses pour A=5, A=8 et A=9, qui sont respectivement -4, -2 et -4.


Question 1b:
Il nous faudrait donc maintenant modifier l'algorithme pour qu'il affiche le reste de la division euclidienne de A²-3A+6 par 4, deux nombres effectivement utilisés par l'algorithme.
Il serait déjà utile de connaître les valeurs du nombre A²-3A+6 afin d'en déduire le reste attendu, et également ce qui ne va pas dans l'algorithme actuel.
Commençons donc par modifier le programme afin d'afficher le nombre A²-3A+6:

Voyons donc maintenant ce que nous obtenons:


Pour A=5, A²-3A+6=16 et le nombre affiché est -4.
Pour A=8, A²-3A+6=46 et le nombre affiché est -2.
Pour A=9, A²-3A+6=60 et le nombre affiché est -4.
On remarque que le nombre N affiché est toujours strictement négatif, ce qui est normal puisque la boucle TantQue se termine sur la condition N<0.
Or, un reste de division euclidienne par 4 est par définition un nombre entier compris entre 0 et 3.
Il y a ici une itération de trop dans la boucle qui soustrait 4, ce qui rend le résultat négatif.
Deux solutions sont envisageables pour corriger cela.
On peut par exemple tout simplement annuler l'itération supplémentaire en ajoutant 4 au résultat:
Afficher la valeur de N+4

On bien, on change le test de la boucle afin qu'elle se termine une itération plus tôt, ce qui est une meilleure solution algorithmique puisqu'on évite des calculs inutiles à la machine:
Tant que N≥4

Dans les deux cas, on obtient désormais les restes attendus, respectivement 0, 2 et 0:


La même chose est bien évidemment réalisable sur TI-Nspire:


... ou encore sur Casio Graph:




Lien:
BAC L 2013: annales des sujets inédits