Correction algo Olympiades Académiques 2013 1ère Besançon
Après l'algorithme des Olympiades Académiques 2013 d'Aix-Marseille dans une news précédente, intéressons-nous maintenant à l'algorithme tombé dans l'Académie de Besançon.
Question I)2):
On nous donne donc un algorithme à trous, destiné à calculer σ(n) pour tout entier naturel n non nul, où σ(n) est la somme de tous les diviseurs de n.
Lorsque le test "le reste de la division euclidienne de n par k est 0" est vérifié, cela veut dire que k est un diviseur de n.
Il faut donc l'ajouter à la somme des diviseurs déjà trouvée.
Il nous faut donc une variable pour cumuler les diviseurs trouvés au fur et à mesure, et c'est la variable σ initialisée à 0, élément neutre de l'addition, qui joue ici ce rôle.
(si on avait du multiplier les valeurs trouvées au lieu de les additionner, on aurait initialisé la variable à 1, élément neutre de la multiplication)
La dernière instruction manquante sera donc "Affecter à σ la valeur σ+k".
Ce test peut être écrit mathématiquement en utilisant la fonction partie entière E introduite en début de Première S.
On peut alors le récrire par exemple "E(n/k)=n/k".
Enfin, k jouant le rôle des diviseurs de n recherchés, on a 1≤k≤n, ce qui nous permet de compléter les bornes de la boucle 'pour':
"Pour k allant de 1 à n faire"
L'algorithme une fois complété nous donne donc:
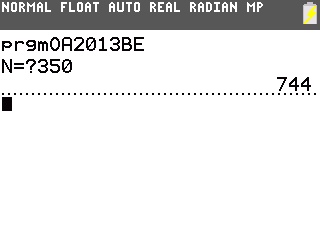
L'on traduit aisément l'algorithme en un programme pour nos TI-82 à TI-84:

Il est alors aisé de vérifier le résultat de la question I)1) précédente: σ(350)=744
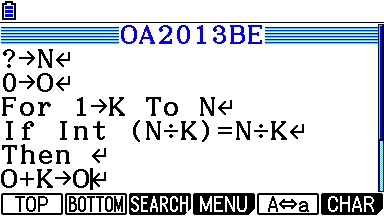
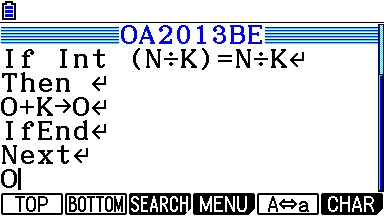
Voici le programme pour Casio Graph/Prizm:
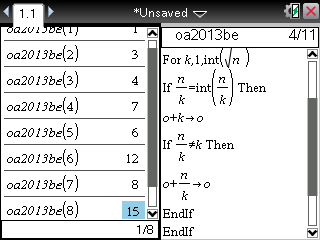
Et voici maintenant le programme pour TI-Nspire:
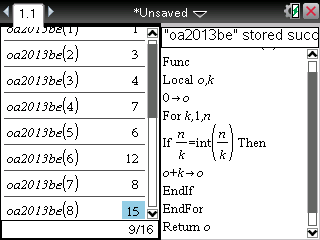
Une fois le programme fonctionnel, il est alors aisé et rapide de déterminer quelques valeurs de σ(n), ce qui va être utile pour les quelques exemples demandés par les questions suivantes!
Question II)1)
Il nous faut donc déterminer justement σ(n) pour n allant de 1 à 6.
Le programme nous répond rapidement que σ(1)=1, σ(2)=3, σ(3)=4, σ(4)=7, σ(5)=6 et σ(6)=12.

Question III)3)a)
Sachant qu'un nombre parfait n vérifie σ(n)=2n, il suffit de faire calculer quelques valeurs supplémentaires au programme:
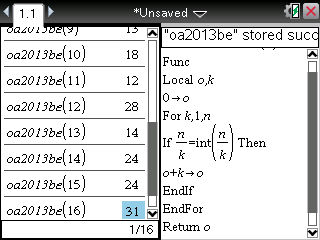
On vérifie alors aisément dans la liste des résultats qu'avec σ(6)=12, 6 est le seul nombre parfait inférieur ou égal à 10.
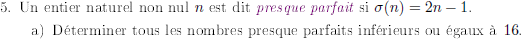
Question III)5)a)
Sachant qu'un nombre presque parfait n vérifie σ(n)=2n-1, on obtient rapidement de façon similaire que les seuls nombres presque parfaits inférieurs ou égaux à 16 sont 1, 2, 4, 8 et 16 avec σ(1)=1, σ(2)=3, σ(4)=7, σ(8)=15 et σ(16)=31.
Tiens, ne seraient-ce pas les puissances de 2?...
Envie de faire un peu plus d'arithmétique et d'algorithmique? Pour une petite 10aine de jours, nous avons encore un concours sur les nombres premiers palindromes!
Lien:
Olympiades Académiques de Mathématiques 2013 - 1ère (Besançon)
Question I)2):
On nous donne donc un algorithme à trous, destiné à calculer σ(n) pour tout entier naturel n non nul, où σ(n) est la somme de tous les diviseurs de n.
Lorsque le test "le reste de la division euclidienne de n par k est 0" est vérifié, cela veut dire que k est un diviseur de n.
Il faut donc l'ajouter à la somme des diviseurs déjà trouvée.
Il nous faut donc une variable pour cumuler les diviseurs trouvés au fur et à mesure, et c'est la variable σ initialisée à 0, élément neutre de l'addition, qui joue ici ce rôle.
(si on avait du multiplier les valeurs trouvées au lieu de les additionner, on aurait initialisé la variable à 1, élément neutre de la multiplication)
La dernière instruction manquante sera donc "Affecter à σ la valeur σ+k".
Ce test peut être écrit mathématiquement en utilisant la fonction partie entière E introduite en début de Première S.
On peut alors le récrire par exemple "E(n/k)=n/k".
Enfin, k jouant le rôle des diviseurs de n recherchés, on a 1≤k≤n, ce qui nous permet de compléter les bornes de la boucle 'pour':
"Pour k allant de 1 à n faire"
L'algorithme une fois complété nous donne donc:
- Code: Select all
Entrée:
n entier naturel non nul
Initialisation:
σ prend la valeur 0
Traitement:
Pour k allant de 1 à n faire
Si E(n/k)=n/k alors
Affecter à σ la valeur σ+k
FinSi
FinPour
Afficher σ
L'on traduit aisément l'algorithme en un programme pour nos TI-82 à TI-84:

Il est alors aisé de vérifier le résultat de la question I)1) précédente: σ(350)=744

Voici le programme pour Casio Graph/Prizm:


Et voici maintenant le programme pour TI-Nspire:

Une fois le programme fonctionnel, il est alors aisé et rapide de déterminer quelques valeurs de σ(n), ce qui va être utile pour les quelques exemples demandés par les questions suivantes!

Question II)1)
Il nous faut donc déterminer justement σ(n) pour n allant de 1 à 6.
Le programme nous répond rapidement que σ(1)=1, σ(2)=3, σ(3)=4, σ(4)=7, σ(5)=6 et σ(6)=12.

Question III)3)a)
Sachant qu'un nombre parfait n vérifie σ(n)=2n, il suffit de faire calculer quelques valeurs supplémentaires au programme:

On vérifie alors aisément dans la liste des résultats qu'avec σ(6)=12, 6 est le seul nombre parfait inférieur ou égal à 10.
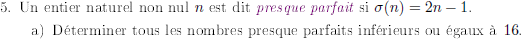
Question III)5)a)
Sachant qu'un nombre presque parfait n vérifie σ(n)=2n-1, on obtient rapidement de façon similaire que les seuls nombres presque parfaits inférieurs ou égaux à 16 sont 1, 2, 4, 8 et 16 avec σ(1)=1, σ(2)=3, σ(4)=7, σ(8)=15 et σ(16)=31.
Tiens, ne seraient-ce pas les puissances de 2?...

Envie de faire un peu plus d'arithmétique et d'algorithmique? Pour une petite 10aine de jours, nous avons encore un concours sur les nombres premiers palindromes!

Lien:
Olympiades Académiques de Mathématiques 2013 - 1ère (Besançon)