Correction algo Olympiades Académiques 2013 1èES/L/Tech Nice
Salut à tous.
En attendant les prochains sujets de BAC fin mai, aujourd'hui continuons à réviser en nous entraînant en algorithmique et programmation avec l'algorithme qui est tombé en exercice 3 pour les Premières ES, L et Technologiques aux Olympiades Académiques dans l'Académie de Nice:

On étudie donc le nombre de cartes nécessaires pour construire un château à n étages.
Question 3:
On nous demande donc à quoi peut bien servir l'algorithme fourni.
Cette question arrivant rapidement en début d'énoncé, on peut se douter qu'il s'agit d'un calcul du nombre de cartes nécessaires.
Cet algorithme utilise de plus une expression factorisée qu'il suffit de développer pour retrouver la formule normalement normalement déterminée à la question 2: 1,5n2+0,5n.
Et même si l'on n'arrivait pas à voir cela, il suffisait de programmer cet algorithme sur nos calculatrices graphiques, et de se rendre compte que les résultats fournis étaient en accord avec ceux du tableau de valeurs de la question 2.
Voici le programme pour toutes les calculatrices TI-82 à TI-84:
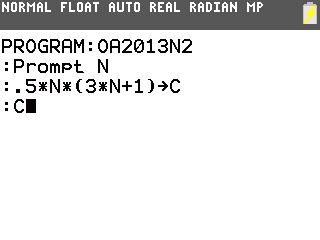
Et effectivement, les résultats sont en accord avec le tableau de valeurs du nombre de cartes nécessaires fourni dans l'énoncé:
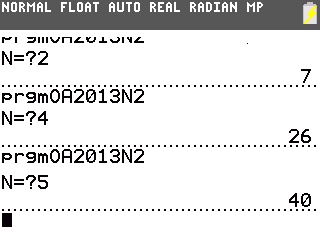
La même chose est réalisable sur nos calculatrices Casio Graph et Casio Prizm...

Ou même encore sur nos TI-Nspire:
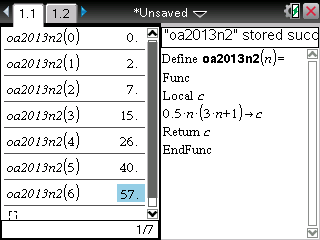
Question 4)a)
Il nous faut donc maintenant créer un algorithme permettant de déterminer le nombre d'étages réalisables avec 500 cartes.
Je vous propose un algorithme autour d'une boucle 'tant que', qui va compter le nombre d'étages en incrémentant un compteur n, tant que l'on ne dépasse pas 500 cartes:
La boucle s'arrêtant lorsque le nombre de cartes 0,5n(3n+1) dépasse strictement 500, en fin de boucle le résultat à afficher n'est pas n mais n-1.
Voici un programme implémentant cet algorithme pour toutes TI-82 à TI-84:

Le programme nous donne même la réponse, 18 étages, qui nous permettra de vérifier notre résultat dans la prochaine question 4)b):
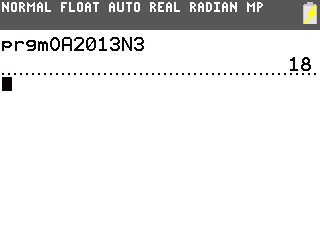
Voici maintenant le programme pour toutes Casio Graph et Casio Prizm, qui heureusement nous confirme le même résultat:


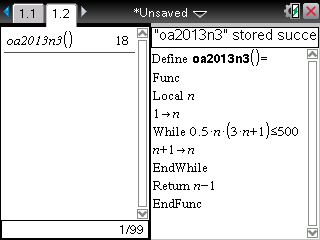
Et voici enfin le programme pour toutes TI-Nspire:
Lien:
Olympiades Académiques 2013 1ère ES/L/Technologiques (Nice)
En attendant les prochains sujets de BAC fin mai, aujourd'hui continuons à réviser en nous entraînant en algorithmique et programmation avec l'algorithme qui est tombé en exercice 3 pour les Premières ES, L et Technologiques aux Olympiades Académiques dans l'Académie de Nice:

On étudie donc le nombre de cartes nécessaires pour construire un château à n étages.
Question 3:
On nous demande donc à quoi peut bien servir l'algorithme fourni.
Cette question arrivant rapidement en début d'énoncé, on peut se douter qu'il s'agit d'un calcul du nombre de cartes nécessaires.
Cet algorithme utilise de plus une expression factorisée qu'il suffit de développer pour retrouver la formule normalement normalement déterminée à la question 2: 1,5n2+0,5n.
Et même si l'on n'arrivait pas à voir cela, il suffisait de programmer cet algorithme sur nos calculatrices graphiques, et de se rendre compte que les résultats fournis étaient en accord avec ceux du tableau de valeurs de la question 2.
Voici le programme pour toutes les calculatrices TI-82 à TI-84:

Et effectivement, les résultats sont en accord avec le tableau de valeurs du nombre de cartes nécessaires fourni dans l'énoncé:

La même chose est réalisable sur nos calculatrices Casio Graph et Casio Prizm...

Ou même encore sur nos TI-Nspire:

Question 4)a)
Il nous faut donc maintenant créer un algorithme permettant de déterminer le nombre d'étages réalisables avec 500 cartes.
Je vous propose un algorithme autour d'une boucle 'tant que', qui va compter le nombre d'étages en incrémentant un compteur n, tant que l'on ne dépasse pas 500 cartes:
- Code: Select all
Traitement:
n prend la valeur 1
Tant que 0,5n(3n+1)≤500
n prend la valeur n+1
Fin tant que
Sortie:
Afficher n-1
La boucle s'arrêtant lorsque le nombre de cartes 0,5n(3n+1) dépasse strictement 500, en fin de boucle le résultat à afficher n'est pas n mais n-1.
Voici un programme implémentant cet algorithme pour toutes TI-82 à TI-84:

Le programme nous donne même la réponse, 18 étages, qui nous permettra de vérifier notre résultat dans la prochaine question 4)b):

Voici maintenant le programme pour toutes Casio Graph et Casio Prizm, qui heureusement nous confirme le même résultat:


Et voici enfin le programme pour toutes TI-Nspire:

A bientôt! 

Lien:
Olympiades Académiques 2013 1ère ES/L/Technologiques (Nice)