Correction algo Olympiades Académiques 1èreS Toulouse
Voici aujourd'hui l'algorithme tombé en exercice 6 aux Olympiades Académiques de 1èreS dans l'Académie de Toulouse.

Il s'agit donc d'un partage d'une sphère selon de grands cercles (sections passant par son centre).
On suppose dans cet énoncé, que les grands cercles sont tous sécants deux à deux.
Question C)2)a):
On nous propose donc un algorithme permettant de déterminer le nombre de régions obtenues après quatre sections de la sphère.
Il nous suffit donc de programmer cet algorithme sur notre calculatrice graphique afin d'obtenir la réponse.
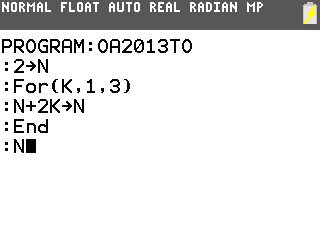
Voici sa traduction en un programme pour calculatrices TI-82 à TI-84:
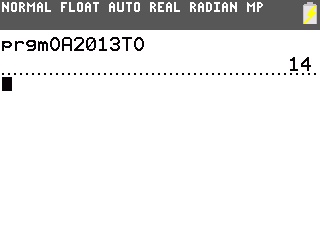
L'exécution du programme nous donne alors la réponse, 14:
Si vous êtes équipés d'une calculatrice Casio Graph/Prizm, vous pouvez sans difficulté réaliser exactement la même chose:


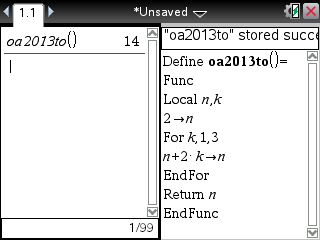
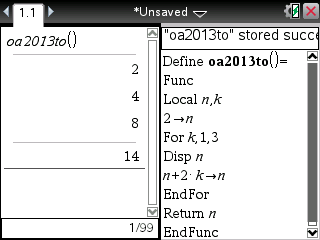
Si vous êtes dotés d'une calculatrice TI-Nspire ou TI-89/92/V200, voici une solution:
Question C)2)b):
L'on nous demande maintenant d'expliquer pourquoi cet algorithme répond bien à la question.
Pour mieux comprendre ce qu'il fait, on pourrait construire la trace de l'algorithme, avec toutes les valeurs intermédiaires prises par la variable NbRegion à chaque passage dans la boucle.
La calculatrice peut nous donner directement cette trace avec l'ajout d'une simple instruction de sortie:
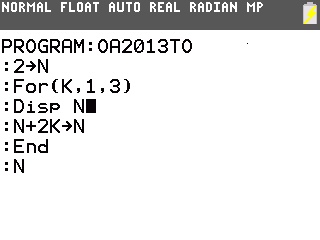

De l'initialisation à la sortie du programme, la variable N prend donc successivement les valeurs 2, 4, 8, 14.
C'est-à-dire que l'on ajoute successivement 2, 4 et 6.
En effet, la valeur initiale 2 est le nombre de régions déterminées par une section selon un grand cercle.
A la 2ème section, les grands cercles étant sécants deux à deux, les deux régions précédentes sont coupées en deux, ce qui nous rajoute 2 régions.
A la 3ème section, le nouveau grand cercle coupe les deux grands cercles précédents, ce qui rajoute 4 régions.
A la 4ème section, le nouveau grand cercle couple les trois grands grands cercles précédents, ce qui rajoute 6 régions.
Le même raisonnement peut être initié à partir d'une Casio Graph /Prizm ou d'une TI-Nspire/89/92/V200:


Lien:
Olympiades Académiques de 1ère 2013 (Académie de Toulouse)

Il s'agit donc d'un partage d'une sphère selon de grands cercles (sections passant par son centre).
On suppose dans cet énoncé, que les grands cercles sont tous sécants deux à deux.
Question C)2)a):
On nous propose donc un algorithme permettant de déterminer le nombre de régions obtenues après quatre sections de la sphère.
Il nous suffit donc de programmer cet algorithme sur notre calculatrice graphique afin d'obtenir la réponse.
Voici sa traduction en un programme pour calculatrices TI-82 à TI-84:

L'exécution du programme nous donne alors la réponse, 14:

Si vous êtes équipés d'une calculatrice Casio Graph/Prizm, vous pouvez sans difficulté réaliser exactement la même chose:


Si vous êtes dotés d'une calculatrice TI-Nspire ou TI-89/92/V200, voici une solution:

Question C)2)b):
L'on nous demande maintenant d'expliquer pourquoi cet algorithme répond bien à la question.
Pour mieux comprendre ce qu'il fait, on pourrait construire la trace de l'algorithme, avec toutes les valeurs intermédiaires prises par la variable NbRegion à chaque passage dans la boucle.
La calculatrice peut nous donner directement cette trace avec l'ajout d'une simple instruction de sortie:


De l'initialisation à la sortie du programme, la variable N prend donc successivement les valeurs 2, 4, 8, 14.
C'est-à-dire que l'on ajoute successivement 2, 4 et 6.
En effet, la valeur initiale 2 est le nombre de régions déterminées par une section selon un grand cercle.
A la 2ème section, les grands cercles étant sécants deux à deux, les deux régions précédentes sont coupées en deux, ce qui nous rajoute 2 régions.
A la 3ème section, le nouveau grand cercle coupe les deux grands cercles précédents, ce qui rajoute 4 régions.
A la 4ème section, le nouveau grand cercle couple les trois grands grands cercles précédents, ce qui rajoute 6 régions.
Le même raisonnement peut être initié à partir d'une Casio Graph /Prizm ou d'une TI-Nspire/89/92/V200:



Lien:
Olympiades Académiques de 1ère 2013 (Académie de Toulouse)