Correction algorithme Maths Obligatoire BAC S 2013 (Liban)
Posted: 28 May 2013, 19:14Ce matin, les candidats au BAC S des lycées français du Liban ont sans surprise eu droit à un algorithme en exercice 4 de leur sujet de Maths Obligatoire, et comme une majorité d'algorithmes du BAC il est posé dans le contexte d'une suite.
Jetons-y un coup d'oeil ce soir:
Question A)1)
On veut donc un algorithme affichant tous les termes d'une suite v, du rang 0 au rang n.
On a la gentillesse dans ce sujet bien sympa de vous proposer 3 algorithmes déjà complets, et simplement de vous demander de choisir le bon.
L'algorithme 1 est à rejeter.
La seule instruction de sortie "Afficher v" arrive en effet après l'instruction "Fin pour". Elle est donc en dehors de la boucle et ne sera exécutée qu'une seule fois. Cet algorithme affichera dans tous les cas 1 seul terme et ne répond pas à la question posée.
L'algorithme 2 est également à rejeter.
L'instruction de sortie "Afficher v" fait suite à une instruction "v prend la valeur 1". Cet algorithme n'affiche donc que des 1 au lieu des valeurs des termes de la suite.
Par élimination, il ne reste donc que l'algorithme 3.
Notons que si vous avez du mal à lire/comprendre les algorithmes, il était également possible de trouver la réponse de façon empirique en utilisant la calculatrice graphique.
L'énoncé a la gentillesse (décidément) de donner en question A)2) ce qu'est censé afficher l'algorithme.
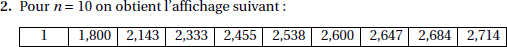
Il suffit donc de programmer les 3 algorithmes et de voir lequel produit le bon affichage.
Voici les 3 programmes pour calculatrices TI-82 à TI-84:
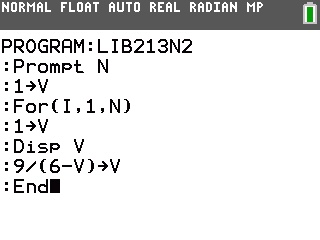
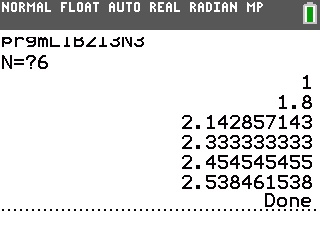
Voici maintenant leurs affichages respectifs:
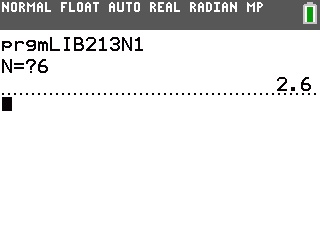
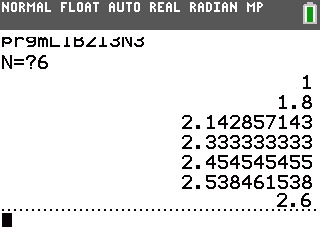
On constate bien les comportements décrits plus haut.
On peut y ajouter une petite précision: l'algorithme 1 affiche bien un seul terme, et il s'agit du terme de rang n.
Si vous êtes munis d'une Casio Graph/Prizm, vous pouvez réaliser la même chose en saisissant les programmes suivants:
Et voici leurs affichages:
Pour le programme 2, l'affichage de 1.8 n'est déclenché par aucune instruction. C'est tout simplement la dernière valeur numérique utilisée dans le programme, que la calculatrice renvoie en tant que résultat, et notamment ici il s'agit de la dernière exécution de l'instruction d'affectation.
Si enfin vous êtes munis d'une TI-Nspire ou TI-89/92/V200, voici les programmes et leurs affichages:
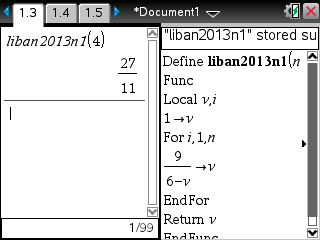
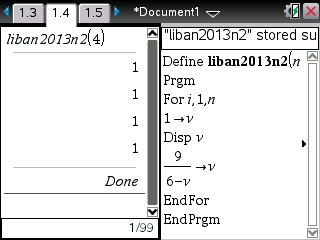
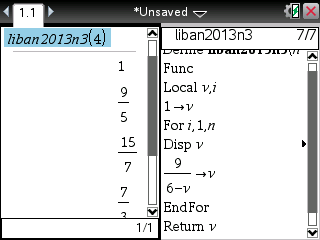
On remarque que le programme 3 affiche des valeurs exactes fractionnaires pour v sur TI-Nspire CAS. Il suffit de provoquer le calcul de v en mode numérique et cela peut se faire par simple utilisation du séparateur décimal dans l'affectation de v:
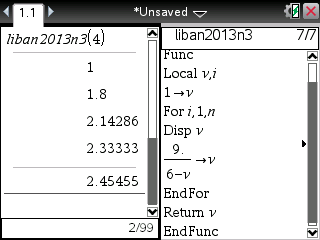
Avant de nous quitter, posons-nous une dernière question au cas où...
Et si l'énoncé n'avait pas donné l'affichage correct de l'algorithme?
Il vous aurait suffi dans ce cas de définir la suite sur votre calculatrice et d'en demander un tableau de valeurs.
Sur TI-82 à TI-84, commencez par passer en mode 'suite' ou 'sequence' en anglais -
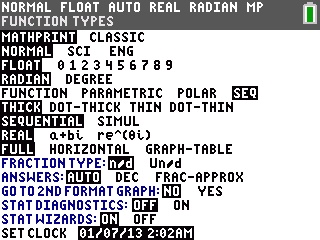
La suite vous est donc définie par une relation de récurrence vn+1=9/(6-vn).
La calculatrice ne vous permet pas de définir le terme de rang n+1 mais uniquement le terme de rang n.
Vous devez donc commencer par réécrire cette relation au rang inférieur, c'est-à-dire en remplaçant tous les 'n' par des 'n-1'.
Cela nous donne vn=9/(6-vn-1)
Une fois cette relation établie, il vous suffit d'aller la saisir -
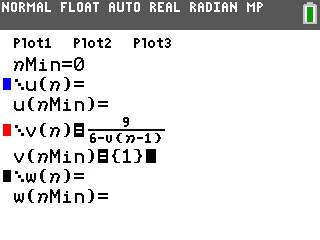
Selon l'état de votre calculatrice, il peut alors être nécessaire de modifier les paramètres du tableau de valeurs, à partir de 0 avec un pas de 1 dans le cas d'une suite -
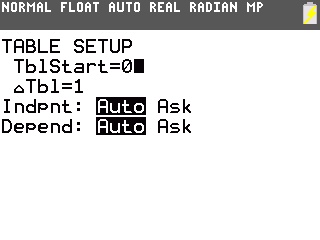
Et vous pouvez enfin demander un tableau de valeurs - 
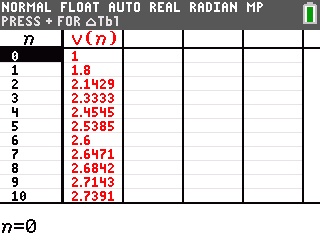
Sur TI-Nspire il vous faut utiliser la même relation.
Dans une application graphique, choisissez un entrée sous forme de suite -
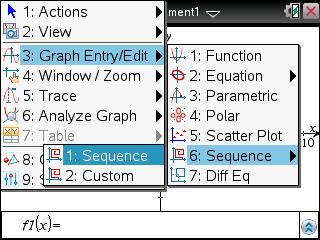
Saisissez alors la relation trouvée plus haut:
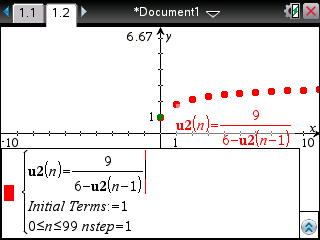
Et demandez enfin le tableau de valeurs -
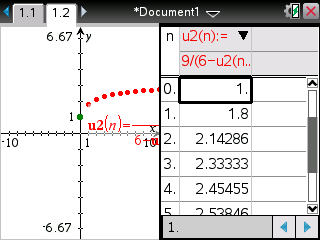
Sur une Casio Graph/Prizm, il suffit d'accéder à l'application 'Recurrence'.
Il est possible ici d'y définir directement le terme de rang n+1!
Mais il ne faut surtout pas oublier de préciser la valeur du terme initial, et cela se fait dans un autre écran accessible via le menu [SET]:
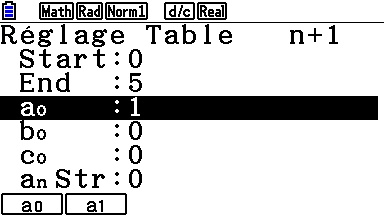
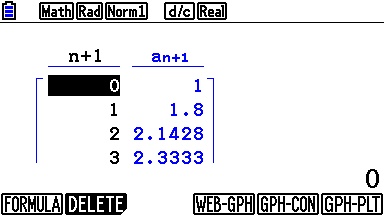
On y précise également les paramètres de notre tableau de valeurs, que voici enfin:
Lien:
Annales des sujets inédits du BAC S 2013 et corrigés
Jetons-y un coup d'oeil ce soir:
Question A)1)
On veut donc un algorithme affichant tous les termes d'une suite v, du rang 0 au rang n.
On a la gentillesse dans ce sujet bien sympa de vous proposer 3 algorithmes déjà complets, et simplement de vous demander de choisir le bon.
L'algorithme 1 est à rejeter.
La seule instruction de sortie "Afficher v" arrive en effet après l'instruction "Fin pour". Elle est donc en dehors de la boucle et ne sera exécutée qu'une seule fois. Cet algorithme affichera dans tous les cas 1 seul terme et ne répond pas à la question posée.
L'algorithme 2 est également à rejeter.
L'instruction de sortie "Afficher v" fait suite à une instruction "v prend la valeur 1". Cet algorithme n'affiche donc que des 1 au lieu des valeurs des termes de la suite.
Par élimination, il ne reste donc que l'algorithme 3.
Notons que si vous avez du mal à lire/comprendre les algorithmes, il était également possible de trouver la réponse de façon empirique en utilisant la calculatrice graphique.
L'énoncé a la gentillesse (décidément) de donner en question A)2) ce qu'est censé afficher l'algorithme.
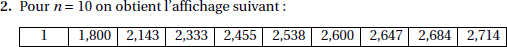
Il suffit donc de programmer les 3 algorithmes et de voir lequel produit le bon affichage.
Voici les 3 programmes pour calculatrices TI-82 à TI-84:
Voici maintenant leurs affichages respectifs:
On constate bien les comportements décrits plus haut.
On peut y ajouter une petite précision: l'algorithme 1 affiche bien un seul terme, et il s'agit du terme de rang n.
Si vous êtes munis d'une Casio Graph/Prizm, vous pouvez réaliser la même chose en saisissant les programmes suivants:
Et voici leurs affichages:
Pour le programme 2, l'affichage de 1.8 n'est déclenché par aucune instruction. C'est tout simplement la dernière valeur numérique utilisée dans le programme, que la calculatrice renvoie en tant que résultat, et notamment ici il s'agit de la dernière exécution de l'instruction d'affectation.
Si enfin vous êtes munis d'une TI-Nspire ou TI-89/92/V200, voici les programmes et leurs affichages:
On remarque que le programme 3 affiche des valeurs exactes fractionnaires pour v sur TI-Nspire CAS. Il suffit de provoquer le calcul de v en mode numérique et cela peut se faire par simple utilisation du séparateur décimal dans l'affectation de v:
Avant de nous quitter, posons-nous une dernière question au cas où...
Et si l'énoncé n'avait pas donné l'affichage correct de l'algorithme?
Il vous aurait suffi dans ce cas de définir la suite sur votre calculatrice et d'en demander un tableau de valeurs.
Sur TI-82 à TI-84, commencez par passer en mode 'suite' ou 'sequence' en anglais -
La suite vous est donc définie par une relation de récurrence vn+1=9/(6-vn).
La calculatrice ne vous permet pas de définir le terme de rang n+1 mais uniquement le terme de rang n.
Vous devez donc commencer par réécrire cette relation au rang inférieur, c'est-à-dire en remplaçant tous les 'n' par des 'n-1'.
Cela nous donne vn=9/(6-vn-1)
Une fois cette relation établie, il vous suffit d'aller la saisir -
Selon l'état de votre calculatrice, il peut alors être nécessaire de modifier les paramètres du tableau de valeurs, à partir de 0 avec un pas de 1 dans le cas d'une suite -
Et vous pouvez enfin demander un tableau de valeurs -
Sur TI-Nspire il vous faut utiliser la même relation.
Dans une application graphique, choisissez un entrée sous forme de suite -
Saisissez alors la relation trouvée plus haut:
Et demandez enfin le tableau de valeurs -
Sur une Casio Graph/Prizm, il suffit d'accéder à l'application 'Recurrence'.
Il est possible ici d'y définir directement le terme de rang n+1!
Mais il ne faut surtout pas oublier de préciser la valeur du terme initial, et cela se fait dans un autre écran accessible via le menu [SET]:
On y précise également les paramètres de notre tableau de valeurs, que voici enfin:
Lien:
Annales des sujets inédits du BAC S 2013 et corrigés
