Correction algorithme Obligatoire BAC S 2013 (Amérique Nord)
En exercice 2 du sujet de Maths Obligatoire qui vient de tomber aujourd'hui pour les candidats au BAC S 2013 dans les lycées français d'Amérique du Nord on a droit on pas à un mais à deux algorithmes, comme bien souvent dans le contexte de suite.
Jetons-y un oeil ensemble cette nuit:
Question 1)a)
On nous demande donc ce qu'affiche l'algorithme lorsque n=3.
Demandons-le donc nous-même à notre tour à notre TI-82 à TI-84, Casio Graph Prizm:
Commençons par programmer l'algorithme:


Sur TI-Nspire CAS et TI-89/92/Voyage 200, il faut utiliser le séparateur décimal dans l'affectation récurrente afin de forcer le mode de calcul numérique approché:
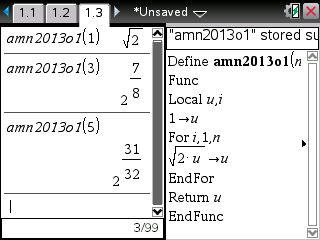
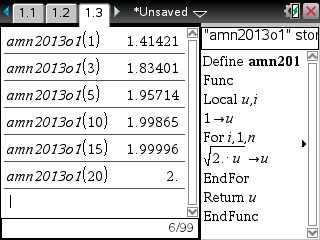
Avons de répondre à la question, on peut avoir l'idée de vérifier le bon fonctionnement de l'algorithme avec les affichages que donnent gentillement la question 1)c)



La valeur est 1,8340 à 10-4 près.
Question 1)b)
On nous demande donc ce que calcule cet algorithme.
L'affectation récurrente "Affecter à u la valeur √(2u)" est la transcription exacte de la relation de récurrence un+1=√(2un).
Lors de l'initialisation il y a bien une affectation "affecter à u la valeur 1" correspondant à u0=1.
Cet algorithme calcule la valeur de un, le terme de rang n de la suite u.
Question 1)b)
La suite semble dans croissante et convergente vers 2.
Question 3)d)
Cet énoncé vous fait ensuite l'honneur d'un deuxième algorithme à la question 3)d):

Il s'agit donc de rechercher le rand du 1er terme de la suite u dépassant strictement 1,999.
Comme on ne sait pas en combien d'essais on va le trouver, il nous faut donc une boucle 'tant que'.
La condition d'arrêt de cette boucle serait donc u>1,999, et la condition de poursuite de la boucle serait donc le contraire: u≤1,999.
Allons-y:
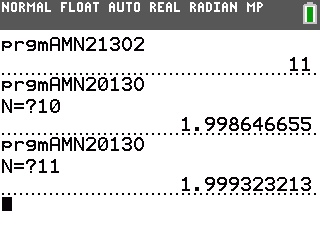
Le tableau de valeurs de la calculatrice nous permet de connaître la réponse: n=11

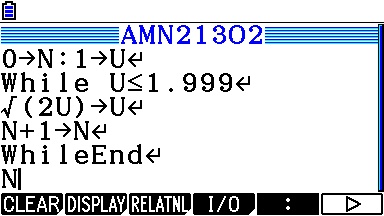
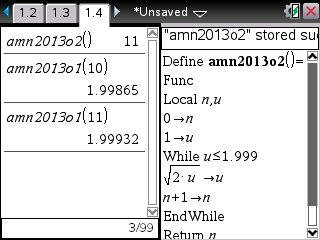
Avant de recopier notre algorithme au propre, on peut donc le programmer sur TI-82 à TI-84, Casio Graph/Prizm ou TI-Nspire/89/92/Voyage200 afin de vérifier qu'il est bien exact:


Lien:
BAC S 2013: Annales des sujets inédits corrigés
Jetons-y un oeil ensemble cette nuit:

Question 1)a)
On nous demande donc ce qu'affiche l'algorithme lorsque n=3.
Demandons-le donc nous-même à notre tour à notre TI-82 à TI-84, Casio Graph Prizm:
Commençons par programmer l'algorithme:


Sur TI-Nspire CAS et TI-89/92/Voyage 200, il faut utiliser le séparateur décimal dans l'affectation récurrente afin de forcer le mode de calcul numérique approché:


Avons de répondre à la question, on peut avoir l'idée de vérifier le bon fonctionnement de l'algorithme avec les affichages que donnent gentillement la question 1)c)



La valeur est 1,8340 à 10-4 près.
Question 1)b)
On nous demande donc ce que calcule cet algorithme.
L'affectation récurrente "Affecter à u la valeur √(2u)" est la transcription exacte de la relation de récurrence un+1=√(2un).
Lors de l'initialisation il y a bien une affectation "affecter à u la valeur 1" correspondant à u0=1.
Cet algorithme calcule la valeur de un, le terme de rang n de la suite u.
Question 1)b)
La suite semble dans croissante et convergente vers 2.
Question 3)d)
Cet énoncé vous fait ensuite l'honneur d'un deuxième algorithme à la question 3)d):

Il s'agit donc de rechercher le rand du 1er terme de la suite u dépassant strictement 1,999.
Comme on ne sait pas en combien d'essais on va le trouver, il nous faut donc une boucle 'tant que'.
La condition d'arrêt de cette boucle serait donc u>1,999, et la condition de poursuite de la boucle serait donc le contraire: u≤1,999.
Allons-y:
- Code: Select all
Variables:
n est un entier naturel
u est un réel
Initialisation:
Affecter à n la valeur 0
Affecter à u la valeur 1
Traitement:
Tant que u≤1,999
Affecter à u la valeur √(2u)
Affecter à n la valeur n+1
Fin du tant que
Afficher n
Le tableau de valeurs de la calculatrice nous permet de connaître la réponse: n=11

Avant de recopier notre algorithme au propre, on peut donc le programmer sur TI-82 à TI-84, Casio Graph/Prizm ou TI-Nspire/89/92/Voyage200 afin de vérifier qu'il est bien exact:





Lien:
BAC S 2013: Annales des sujets inédits corrigés