Forum TI-Planet.org

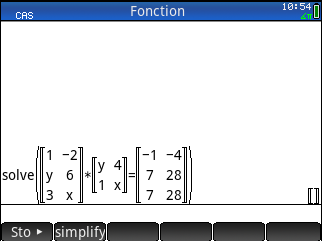
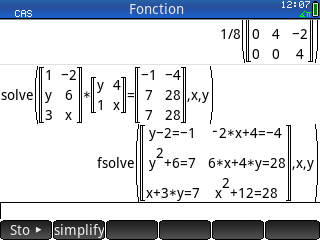
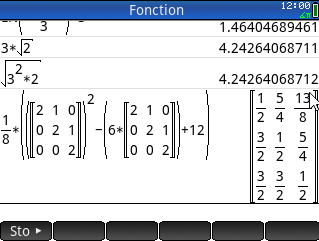
Bonsoir, j'aimerais résoudre des équations matricielles dans le CAS avec ma HP Prime G2, seulement, j'ai un problème avec la syntaxe. Je sais qu'il faut indiquer les inconnues entre crochets mais je ne vois pas comment les insérer car le raccourcis crochets créée lui-même une matrice, et faire une matrice ligne listant les inconnues ne fonctionne pas.

Pouvez vous m'aider ?

Merci d'avance

Les types d'équations matricielles sont différentes. Présentez votre exemple d'équation matricielle à résoudre.

par exemple :

Je ne connais rien au calcul matriciel mais as-tu préciser x et y en arguments de solve ?
solve(équations,x,y)

Merci, ça aide mais serait-il possible d'avoir directement les résultats?



Autre question: pourquoi deux calculs donnent-ils deux résultats différents dans le CAS et le HOME?

Gordra wrote:Merci, ça aide mais serait-il possible d'avoir directement les résultats?



Autre question: pourquoi deux calculs donnent-ils deux résultats différents dans le CAS et le HOME?

EDIT : je voulais dire "le même calcul" dans la deuxième question

Pour resoudre le systeme, il faut passer la liste des inconnues en 2eme argument de solve:

Code: Select all

solve([[1,-2],[y,6],[3,x]]*[[y,4],[1,x]]=[[-1,-4],[7,28],[7,28]],[x,y])

Le resultat du calcul matriciel est different entre HOME et CAS parce que la somme d'une matrice et d'un scalaire n'est pas definie mathematiquement parlant. Dans CAS, j'ai fait le choix qui est le plus naturel pour un mathematicien, a savoir considerer le scalaire comme etant scalaire*matrice identite (ca n'a evidemment de sens que si la matrice est carree), ce qui permet d'appliquer des polynomes a une matrice. Notez que vous pouvez utiliser la commande horner pour faire cela, par exemple dans votre cas

Code: Select all

horner(1/8*(x^2-6x+12),[[2,1,0],[0,2,1],[0,0,2]])