IA Synchro-donjon #2 : Recherche de chemin
Dans le cadre de notre concours de rentrée 2021 avec TI-Planet, nous te proposons de résoudre deux jeux codés en Python avec ta calculatrice graphique : La geste d'Alrys et Synchro-donjon. 
Pour t'aider à aborder Synchro-donjon et à apprendre des choses nouvelles sur la programmation et l'intelligence artificielle, je te présente en détail les IAs groupées avec le programme, de la plus simple à une modérément perfectionnée. Aujourd'hui, on regarde ia2_path.py !
N'oublie pas de lire les règles de Synchro-donjon et de tester le programme sur ta calculatrice avant de lire cet article, sinon tu seras vite perdu·e !
Allez voilà, je te mets le code entier ici si tu veux tenter de le lire tout seul, et puis on va expliquer ce qui se passe et le tester ensemble.
Le principe de cette IA est tout simple : on fait sortir chaque joueur dans l'ordre.
Voyons comment on code cette IA !
Notre IA a une stratégie "globale" qui dure toute la partie : elle traite les joueurs dans un ordre défini : Jaune, Rouge, Bleu, Vert. Elle doit donc se souvenir d'où elle en est quand on lui demande sa prochaine action.
Il faut donc avoir des variables qui gardent leur valeur entre deux appel à notre fonction tour(), et pour ça on va utiliser des variables globales.
Ton professeur d'informatique/NSI t'as probablement enseigné qu'utiliser des variables globales est souvent un mauvais choix. Il/elle a raison ! Ici je m'en sers parce que les autres options compliqueraient beaucoup le code.
Comme tu peux le voir, j'ai créé deux variables joueur_courant et chemin, et elles sont globales parce qu'elles ne sont pas dans une fonction. Dans la fonction tour() où je vais coder notre IA, j'indique à Python que je veux les utiliser avec la commande global, sinon Python refuserait de les modifier.
Avec ça, on peut commencer à jouer !
Pour trouver un chemin, on peut utiliser la fonction calculer_chemin() qui est fournie par synchrod.py. Son fonctionnement est le suivant :
Le plateau est celui qui est donné en premier paramètre de tour() (il n'y en a qu'un de toute façon !). Les cases de depart et d'arrivée sont des nombres entiers, comme on a vu dans la présentation du problème.
La réponse de calculer_chemin() est une liste de directions qui emmène de le case de départ à la case d'arrivée (et c'est le plus court chemin possible !). Mais comme une image vaut 1000 mots, voici le premier niveau que synchrod.py te donne (si tu ne changes pas la génération aléatoire) :
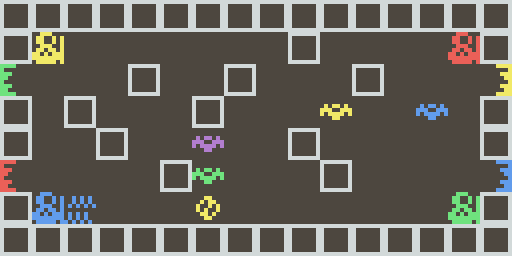
On veut emmener Jaune de sa position initiale (ligne 1, colonne 1, de valeur 16×1+1=17) à sa sortie (ligne 2, colonne 15, de valeur 16×2+15=47). On appelle donc :
Et la liste qu'on récupère est la suivante :
On peut visualiser le chemin comme ceci (cette visualisation utilise une version modifiée de synchrod.py).
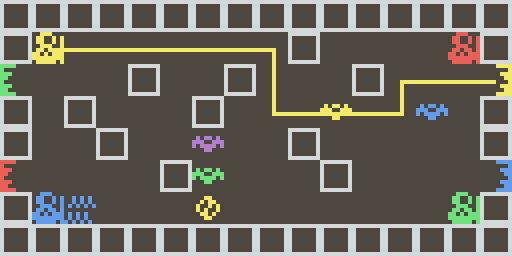
Voilà une base solide ! Maintenant, comment est-ce qu'on utilise la liste ?
Voilà l'idée : la variable globale chemin va indiquer quelle chemin il nous reste à parcourir. Comme ça, à chaque tour, on peut choisir comme action le premier mouvement du chemin, retirer ce mouvement de la liste, et tout sera prêt pour le prochain tour !
C'est ce qu'on fait à la fin de la fonction :
Maintenant, il reste à agencer tout ça pour que tout le monde puisse sortir, pas juste Jaune.
On a quatre joueurs à faire sortir : Jaune, Rouge, Bleu et Vert (qui sont représentés par quatre entiers 0, 1, 2 et 3). C'est pour ça qu'on a deux variables globales :
Au début du tour, la première chose à faire est de tester si le joueur courant vient de sortir. On peut le savoir en inspectant la liste joueurs (le deuxième paramètre de tour()), qui indique la position de chaque joueur. Cette position est un nombre entre 0 et 127 si le joueur est sur le plateau, et vaut -1 si le joueur est sorti.
Donc, si le joueur courant est sorti, on passe au suivant et on réinitialise chemin pour bien le recalculer.
Il y a une subtilité, cela dit : parfois deux joueurs peuvent sortir en même temps (si Vert et Bleu sont tous les deux à gauche de leur sortie et qu'on choisit ALLER_DROITE par exemple). Dans ce cas, joueur_courant+=1 n'est pas suffisant, parce que joueur_courant+1 est peut-être déjà sorti !
Pour éviter ça, on change le if en while, comme ça si joueur_courant+1 est déjà sorti, eh bien on passe au suivant !
Il ne reste plus qu'à calculer le chemin à prendre quand chemin=[]. (On pourrait le calculer à chaque tour, mais c'est inutile : le chemin reste le même jusqu'à ce que le joueur courant soit sorti !)
Comme précédemment, j'utilise calculer_chemin(). Comme case de départ, on prend la position du joueur courant, et comme case d'arrivée, la position sur le plateau de sa sortie. .index() est une méthode de liste qui te donne la position dans la liste d'une valeur choisie, ce qui te permet ici de chercher des objets sur le plateau.
Avec ça, l'IA est presque complète !
La fonction play_game() réalise toute une série de parties en une seule exécution du programme (par défaut, 100). Il faut donc s'assurer que l'IA est nettoyée entre chaque partie sinon les variables seront fausses.
Pour ça, on peut utiliser le troisième et dernier paramètres de la fonction tour : la liste evenements. Cette liste indique ce qui se passe sur le plateau, et t'informe de quand les nouvelles parties commencent (et des effets des pièges).
Au début de l'IA, on prend donc soin de réinitialiser nos deux variables globales à chaque début de partie, pour pas que les valeurs de la partie précédente ne viennent perturber le code.
Et voilà ! Avec tout ça, le code est complet. Tu peux le voir de nouveau en entier :
Il est temps de lancer cette IA et de voir de quoi elle est capable. Ce qui est sûr c'est que la méthode de faire sortir chaque joueur dans l'ordre doit permettre de résoudre toutes les plateaux (pas forcément rapidement).
Lançons ia2_path.py... voilà ce que ça donne en interactif !
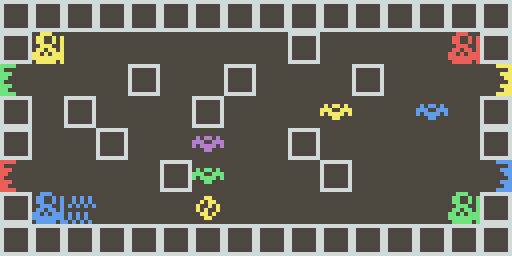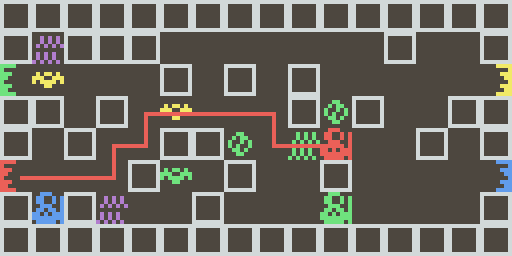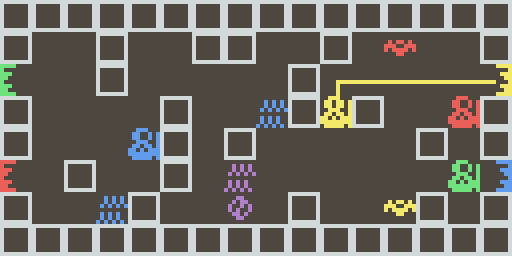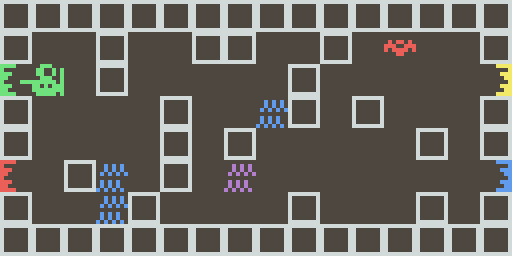
C'est pas mal du tout. Et voilà le résultat dans la console :
Bingo ! Comme tu peux le voir, tous les plateaux ont été résolus. Il y a plein de plateaux où le résultat est très mauvais (négatif, ce qui ajoute 0 au score), et on prend beaucoup de dégâts à cause des pièges et des monstres, mais c'est un bon début !
Le score de cette IA n'est pas moins de 2171, soit presque 22 points par plateau. La prochaine fois, on verra comment de toutes petites améliorations sur ce code permettent de faire un score beaucoup, beaucoup plus élevé. o/

Pour t'aider à aborder Synchro-donjon et à apprendre des choses nouvelles sur la programmation et l'intelligence artificielle, je te présente en détail les IAs groupées avec le programme, de la plus simple à une modérément perfectionnée. Aujourd'hui, on regarde ia2_path.py !
N'oublie pas de lire les règles de Synchro-donjon et de tester le programme sur ta calculatrice avant de lire cet article, sinon tu seras vite perdu·e !

Allez voilà, je te mets le code entier ici si tu veux tenter de le lire tout seul, et puis on va expliquer ce qui se passe et le tester ensemble.

- Code: Select all
from polycal4 import get_infos
from synchrod import *
# Joueur qu'on veut sortir
joueur_courant = 0
# Chemin pour le sortir
chemin = []
def tour(plateau, joueurs, evenements):
global joueur_courant, chemin
# Réinitialisation en début de partie
for (x, y, ev, joueur) in evenements:
if ev == NOUVELLE_PARTIE:
joueur_courant = 0
chemin = []
# Si le joueur est arrivé à sa destination, on passe au suivant.
# Il arrive que plusieurs joueurs sortent en un seul tour, si ça se produit
# on continue de passer au joueur suivant (il en reste forcément un qui
# n'est pas sorti sinon la partie serait finie).
while joueurs[joueur_courant] == -1:
joueur_courant += 1
chemin = []
# Chemin du joueur actuel vers sa sortie
if chemin == []:
case_sortie = plateau.index(SORTIE + joueur_courant)
chemin = calculer_chemin(plateau, joueurs[joueur_courant], case_sortie)
# Prochaine étape
mouvement = chemin[0]
chemin = chemin[1:]
return mouvement
play_game(tour, blind=True)
Le principe de cette IA est tout simple : on fait sortir chaque joueur dans l'ordre.

- D'abord on détermine le chemin pour emmener Jaune de sa position initiale à sa sortie.
- À chaque tour on donne une étape du chemin jusqu'à ce que Jaune soit sorti.
- À ce moment-là, on détermine le chemin pour emmener Rouge de sa position courante jusqu'à sa sortie, et on refait pareil.
- Une fois Rouge sorti, on fait la même chose pour Bleu et Vert.
Voyons comment on code cette IA !

Conserver des informations entre chaque tour
Notre IA a une stratégie "globale" qui dure toute la partie : elle traite les joueurs dans un ordre défini : Jaune, Rouge, Bleu, Vert. Elle doit donc se souvenir d'où elle en est quand on lui demande sa prochaine action.
Il faut donc avoir des variables qui gardent leur valeur entre deux appel à notre fonction tour(), et pour ça on va utiliser des variables globales.

Ton professeur d'informatique/NSI t'as probablement enseigné qu'utiliser des variables globales est souvent un mauvais choix. Il/elle a raison ! Ici je m'en sers parce que les autres options compliqueraient beaucoup le code.
- Code: Select all
joueur_courant = 0
chemin = []
def tour(plateau, joueurs, evenements):
global joueur_courant, chemin
# ... Notre IA ...
Comme tu peux le voir, j'ai créé deux variables joueur_courant et chemin, et elles sont globales parce qu'elles ne sont pas dans une fonction. Dans la fonction tour() où je vais coder notre IA, j'indique à Python que je veux les utiliser avec la commande global, sinon Python refuserait de les modifier.
Avec ça, on peut commencer à jouer !
Trouver et exploiter un chemin pour sortir Jaune
Pour trouver un chemin, on peut utiliser la fonction calculer_chemin() qui est fournie par synchrod.py. Son fonctionnement est le suivant :
- Code: Select all
chemin = calculer_chemin(plateau, case_de_depart, case_d_arrivee)
Le plateau est celui qui est donné en premier paramètre de tour() (il n'y en a qu'un de toute façon !). Les cases de depart et d'arrivée sont des nombres entiers, comme on a vu dans la présentation du problème.

La réponse de calculer_chemin() est une liste de directions qui emmène de le case de départ à la case d'arrivée (et c'est le plus court chemin possible !). Mais comme une image vaut 1000 mots, voici le premier niveau que synchrod.py te donne (si tu ne changes pas la génération aléatoire) :

On veut emmener Jaune de sa position initiale (ligne 1, colonne 1, de valeur 16×1+1=17) à sa sortie (ligne 2, colonne 15, de valeur 16×2+15=47). On appelle donc :
- Code: Select all
chemin = calculer_chemin(plateau, 17, 47)
Et la liste qu'on récupère est la suivante :
- Code: Select all
chemin
# [ALLER_DROITE, ALLER_DROITE, ALLER_DROITE, ALLER_DROITE,
# ALLER_DROITE, ALLER_DROITE, ALLER_DROITE, ALLER_BAS,
# ALLER_BAS, ALLER_DROITE, ALLER_DROITE, ALLER_DROITE,
# ALLER_DROITE, ALLER_HAUT, ALLER_DROITE, ALLER_DROITE,
# ALLER_DROITE]
On peut visualiser le chemin comme ceci (cette visualisation utilise une version modifiée de synchrod.py).

Voilà une base solide ! Maintenant, comment est-ce qu'on utilise la liste ?
Voilà l'idée : la variable globale chemin va indiquer quelle chemin il nous reste à parcourir. Comme ça, à chaque tour, on peut choisir comme action le premier mouvement du chemin, retirer ce mouvement de la liste, et tout sera prêt pour le prochain tour !
C'est ce qu'on fait à la fin de la fonction :
- Code: Select all
mouvement = chemin[0]
chemin = chemin[1:]
return mouvement
Maintenant, il reste à agencer tout ça pour que tout le monde puisse sortir, pas juste Jaune.

Traiter tous les joueurs dans l'ordre
On a quatre joueurs à faire sortir : Jaune, Rouge, Bleu et Vert (qui sont représentés par quatre entiers 0, 1, 2 et 3). C'est pour ça qu'on a deux variables globales :
- joueur_courant indique quel joueur on est en train de faire sortir.
- chemin indique quels mouvements ils restent pour qu'il sorte. Si chemin est vide c'est qu'on ne l'a pas encore calculé.
Au début du tour, la première chose à faire est de tester si le joueur courant vient de sortir. On peut le savoir en inspectant la liste joueurs (le deuxième paramètre de tour()), qui indique la position de chaque joueur. Cette position est un nombre entre 0 et 127 si le joueur est sur le plateau, et vaut -1 si le joueur est sorti.
Donc, si le joueur courant est sorti, on passe au suivant et on réinitialise chemin pour bien le recalculer.
- Code: Select all
if joueurs[joueur_courant] == -1:
joueur_courant += 1
chemin = []
Il y a une subtilité, cela dit : parfois deux joueurs peuvent sortir en même temps (si Vert et Bleu sont tous les deux à gauche de leur sortie et qu'on choisit ALLER_DROITE par exemple). Dans ce cas, joueur_courant+=1 n'est pas suffisant, parce que joueur_courant+1 est peut-être déjà sorti !
Pour éviter ça, on change le if en while, comme ça si joueur_courant+1 est déjà sorti, eh bien on passe au suivant !
- Code: Select all
while joueurs[joueur_courant] == -1:
joueur_courant += 1
chemin = []
Il ne reste plus qu'à calculer le chemin à prendre quand chemin=[]. (On pourrait le calculer à chaque tour, mais c'est inutile : le chemin reste le même jusqu'à ce que le joueur courant soit sorti !)
- Code: Select all
if chemin == []:
case_sortie = plateau.index(SORTIE + joueur_courant)
chemin = calculer_chemin(plateau, joueurs[joueur_courant], case_sortie)
Comme précédemment, j'utilise calculer_chemin(). Comme case de départ, on prend la position du joueur courant, et comme case d'arrivée, la position sur le plateau de sa sortie. .index() est une méthode de liste qui te donne la position dans la liste d'une valeur choisie, ce qui te permet ici de chercher des objets sur le plateau.

Avec ça, l'IA est presque complète !
Rénitialiser à chaque nouvelle partie
La fonction play_game() réalise toute une série de parties en une seule exécution du programme (par défaut, 100). Il faut donc s'assurer que l'IA est nettoyée entre chaque partie sinon les variables seront fausses.
Pour ça, on peut utiliser le troisième et dernier paramètres de la fonction tour : la liste evenements. Cette liste indique ce qui se passe sur le plateau, et t'informe de quand les nouvelles parties commencent (et des effets des pièges).
Au début de l'IA, on prend donc soin de réinitialiser nos deux variables globales à chaque début de partie, pour pas que les valeurs de la partie précédente ne viennent perturber le code.

- Code: Select all
for (x, y, ev, joueur) in evenements:
if ev == NOUVELLE_PARTIE:
joueur_courant = 0
chemin = []
Et voilà ! Avec tout ça, le code est complet. Tu peux le voir de nouveau en entier :
- Code: Select all
from polycal4 import get_infos
from synchrod import *
# Joueur qu'on veut sortir
joueur_courant = 0
# Chemin pour le sortir
chemin = []
def tour(plateau, joueurs, evenements):
global joueur_courant, chemin
# Réinitialisation en début de partie
for (x, y, ev, joueur) in evenements:
if ev == NOUVELLE_PARTIE:
joueur_courant = 0
chemin = []
# Si le joueur est arrivé à sa destination, on passe au suivant.
# Il arrive que plusieurs joueurs sortent en un seul tour, si ça se produit
# on continue de passer au joueur suivant (il en reste forcément un qui
# n'est pas sorti sinon la partie serait finie).
while joueurs[joueur_courant] == -1:
joueur_courant += 1
chemin = []
# Chemin du joueur actuel vers sa sortie
if chemin == []:
case_sortie = plateau.index(SORTIE + joueur_courant)
chemin = calculer_chemin(plateau, joueurs[joueur_courant], case_sortie)
# Prochaine étape
mouvement = chemin[0]
chemin = chemin[1:]
return mouvement
play_game(tour, blind=True)
L'IA en action
Il est temps de lancer cette IA et de voir de quoi elle est capable. Ce qui est sûr c'est que la méthode de faire sortir chaque joueur dans l'ordre doit permettre de résoudre toutes les plateaux (pas forcément rapidement).
Lançons ia2_path.py... voilà ce que ça donne en interactif !

C'est pas mal du tout. Et voilà le résultat dans la console :
- Code: Select all
#0: 12648430
Bravo! 39T 50D -> 61
#1: 594213422
Bravo! 75T 90D -> -15
#2: 236840551
Bravo! 80T 50D -> 20
#3: 2464859390
Bravo! 73T 90D -> -13
#4: 3280879791
Bravo! 87T 70D -> -7
#5: 3426230116
Bravo! 92T 120D -> -62
#6: 2269403964
Bravo! 64T 140D -> -54
#7: 1618746239
Bravo! 77T 30D -> 43
#8: 1236680090
Bravo! 80T 60D -> 10
#9: 3351370485
Bravo! 68T 80D -> 2
#10: 553563167
Bravo! 68T 10D -> 72
#11: 2315605486
Bravo! 72T 30D -> 48
#12: 1036554885
Bravo! 74T 30D -> 46
#13: 1875589748
Bravo! 62T 40D -> 48
#14: 2184596687
Bravo! 64T 80D -> 6
#15: 541455511
Bravo! 71T 80D -> -1
#16: 167669688
Bravo! 81T 70D -> -1
#17: 4207823168
Bravo! 97T 120D -> -67
#18: 1105457756
Bravo! 82T 50D -> 18
#19: 2614210402
Bravo! 58T 50D -> 42
#20: 2529202849
Bravo! 81T 50D -> 19
#21: 3055039143
Bravo! 68T 60D -> 22
#22: 2127226719
Bravo! 83T 130D -> -63
#23: 3082902456
Bravo! 41T 90D -> 19
#24: 4205257665
Bravo! 82T 30D -> 38
#25: 199407319
Bravo! 72T 30D -> 48
#26: 3746711289
Bravo! 83T 40D -> 27
#27: 878032796
Bravo! 74T 30D -> 46
#28: 4092570800
Bravo! 64T 30D -> 56
#29: 2286764744
Bravo! 66T 130D -> -46
#30: 1171391719
Bravo! 64T 110D -> -24
#31: 2776227355
Bravo! 78T 20D -> 52
#32: 894346068
Bravo! 63T 20D -> 67
#33: 4198606884
Bravo! 72T 90D -> -12
#34: 1999695195
Bravo! 72T 60D -> 18
#35: 3064761848
Bravo! 77T 70D -> 3
#36: 1746501463
Bravo! 60T 70D -> 20
#37: 3486740195
Bravo! 76T 160D -> -86
#38: 1456243622
Bravo! 70T 70D -> 10
#39: 4011916507
Bravo! 90T 40D -> 20
#40: 3151169566
Bravo! 80T 60D -> 10
#41: 940545148
Bravo! 71T 40D -> 39
#42: 3446077346
Bravo! 64T 80D -> 6
#43: 883263786
Bravo! 78T 70D -> 2
#44: 394521061
Bravo! 67T 20D -> 63
#45: 3141843215
Bravo! 66T 40D -> 44
#46: 1333750067
Bravo! 83T 90D -> -23
#47: 596029757
Bravo! 64T 60D -> 26
#48: 4053873450
Bravo! 81T 40D -> 29
#49: 716746680
Bravo! 64T 90D -> -4
#50: 1252794865
Bravo! 79T 70D -> 1
#51: 3501098597
Bravo! 78T 50D -> 22
#52: 3328255349
Bravo! 77T 20D -> 53
#53: 1238029435
Bravo! 85T 80D -> -15
#54: 3864774413
Bravo! 70T 50D -> 30
#55: 1518239785
Bravo! 85T 30D -> 35
#56: 91852842
Bravo! 64T 100D -> -14
#57: 3878397276
Bravo! 69T 100D -> -19
#58: 782363206
Bravo! 90T 20D -> 40
#59: 1793375283
Bravo! 85T 50D -> 15
#60: 3387026551
Bravo! 59T 40D -> 51
#61: 1748811549
Bravo! 66T 190D -> -106
#62: 2533799161
Bravo! 64T 50D -> 36
#63: 404853182
Bravo! 74T 60D -> 16
#64: 3616886901
Bravo! 66T 50D -> 34
#65: 2377478389
Bravo! 74T 80D -> -4
#66: 520238391
Bravo! 81T 50D -> 19
#67: 3718574493
Bravo! 96T 110D -> -56
#68: 832990622
Bravo! 81T 30D -> 39
#69: 428843202
Bravo! 79T 30D -> 41
#70: 769357530
Bravo! 75T 30D -> 45
#71: 3649605739
Bravo! 66T 80D -> 4
#72: 3740321927
Bravo! 66T 120D -> -36
#73: 3852969101
Bravo! 79T 80D -> -9
#74: 3256289293
Bravo! 64T 70D -> 16
#75: 3038448294
Bravo! 63T 90D -> -3
#76: 904654193
Bravo! 87T 40D -> 23
#77: 2018615892
Bravo! 75T 80D -> -5
#78: 2794925654
Bravo! 66T 110D -> -26
#79: 3312369991
Bravo! 71T 100D -> -21
#80: 241453064
Bravo! 70T 20D -> 60
#81: 109767354
Bravo! 68T 20D -> 62
#82: 4168036525
Bravo! 83T 100D -> -33
#83: 2534421228
Bravo! 85T 40D -> 25
#84: 2185394352
Bravo! 86T 10D -> 54
#85: 3553770696
Bravo! 108T 150D -> -108
#86: 2393592041
Bravo! 76T 70D -> 4
#87: 1625609068
Bravo! 64T 60D -> 26
#88: 3540367519
Bravo! 64T 50D -> 36
#89: 2216609637
Bravo! 66T 100D -> -16
#90: 2291443810
Bravo! 68T 60D -> 22
#91: 4284680541
Bravo! 72T 40D -> 38
#92: 3688132900
Bravo! 70T 30D -> 50
#93: 4091713635
Bravo! 68T 10D -> 72
#94: 4216499651
Bravo! 76T 110D -> -36
#95: 1079331201
Bravo! 70T 130D -> -50
#96: 2738161974
Bravo! 73T 60D -> 17
#97: 2206455251
Bravo! 85T 30D -> 35
#98: 3529942408
Bravo! 83T 140D -> -73
#99: 2009880399
Bravo! 80T 20D -> 50
Games solved: 100
Score: 2171
Bingo ! Comme tu peux le voir, tous les plateaux ont été résolus. Il y a plein de plateaux où le résultat est très mauvais (négatif, ce qui ajoute 0 au score), et on prend beaucoup de dégâts à cause des pièges et des monstres, mais c'est un bon début !

Le score de cette IA n'est pas moins de 2171, soit presque 22 points par plateau. La prochaine fois, on verra comment de toutes petites améliorations sur ce code permettent de faire un score beaucoup, beaucoup plus élevé. o/
