formulaire RDM
DownloadTélécharger
Actions
Vote :
ScreenshotAperçu
Informations
Catégorie :Category: mViewer GX Creator Lua TI-Nspire
Auteur Author: euskadi77
Type : Classeur 3.6
Page(s) : 3
Taille Size: 232.28 Ko KB
Mis en ligne Uploaded: 26/03/2015 - 10:30:18
Mis à jour Updated: 26/03/2015 - 11:27:45
Uploadeur Uploader: euskadi77 (Profil)
Téléchargements Downloads: 192
Visibilité Visibility: Archive publique
Shortlink : http://ti-pla.net/a177855
Type : Classeur 3.6
Page(s) : 3
Taille Size: 232.28 Ko KB
Mis en ligne Uploaded: 26/03/2015 - 10:30:18
Mis à jour Updated: 26/03/2015 - 11:27:45
Uploadeur Uploader: euskadi77 (Profil)
Téléchargements Downloads: 192
Visibilité Visibility: Archive publique
Shortlink : http://ti-pla.net/a177855
Description
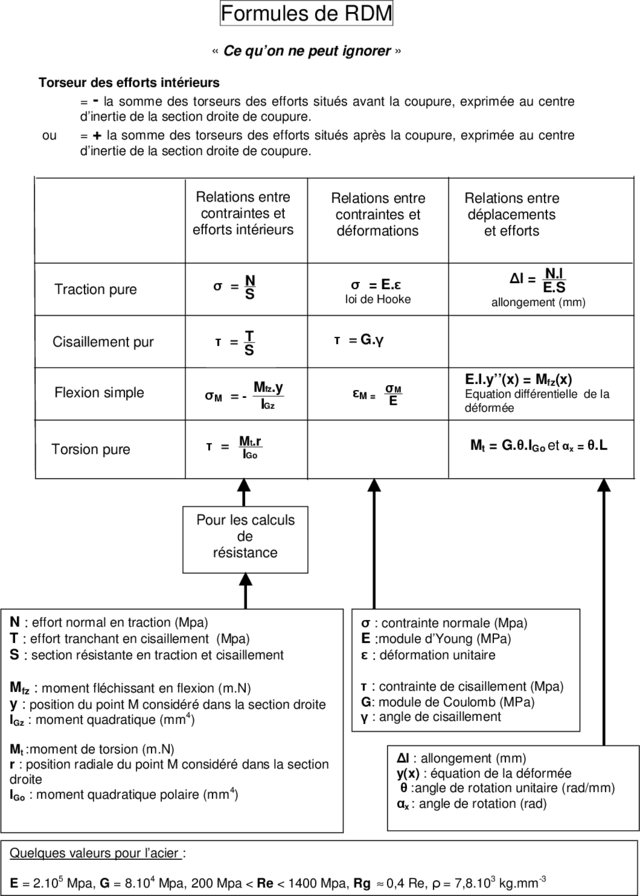
Formules de RDM
« Ce qu’on ne peut ignorer »
Torseur des efforts intérieurs
= - la somme des torseurs des efforts situés avant la coupure, exprimée au centre
d’inertie de la section droite de coupure.
ou = + la somme des torseurs des efforts situés après la coupure, exprimée au centre
d’inertie de la section droite de coupure.
Relations entre Relations entre Relations entre
contraintes et contraintes et déplacements
efforts intérieurs déformations et efforts
= N = E. l = N.l
Traction pure S E. S
loi de Hooke allongement (mm)
Cisaillement pur = T = G.
S
E.I.y’’(x) = Mfz(x)
Flexion simple Mfz.y M
M =- M=
E
Equation différentielle de la
IGz déformée
Torsion pure = Mt.r Mt = G. .IGo et x = .L
IGo
Pour les calculs
de
résistance
N : effort normal en traction (Mpa) : contrainte normale (Mpa)
T : effort tranchant en cisaillement (Mpa) E :module d’Young (MPa)
S : section résistante en traction et cisaillement : déformation unitaire
Mfz : moment fléchissant en flexion (m.N) : contrainte de cisaillement (Mpa)
y : position du point M considéré dans la section droite G: module de Coulomb (MPa)
IGz : moment quadratique (mm4) : angle de cisaillement
Mt :moment de torsion (m.N)
r : position radiale du point M considéré dans la section l : allongement (mm)
droite y(x) : équation de la déformée
:angle de rotation unitaire (rad/mm)
IGo : moment quadratique polaire (mm 4)
x : angle de rotation (rad)
Quelques valeurs pour l’acier :
E = 2.105 Mpa, G = 8.104 Mpa, 200 Mpa < Re < 1400 Mpa, Rg ≈ 0,4 Re, = 7,8.103 kg.mm-3
« Ce qu’on ne peut ignorer »
Torseur des efforts intérieurs
= - la somme des torseurs des efforts situés avant la coupure, exprimée au centre
d’inertie de la section droite de coupure.
ou = + la somme des torseurs des efforts situés après la coupure, exprimée au centre
d’inertie de la section droite de coupure.
Relations entre Relations entre Relations entre
contraintes et contraintes et déplacements
efforts intérieurs déformations et efforts
= N = E. l = N.l
Traction pure S E. S
loi de Hooke allongement (mm)
Cisaillement pur = T = G.
S
E.I.y’’(x) = Mfz(x)
Flexion simple Mfz.y M
M =- M=
E
Equation différentielle de la
IGz déformée
Torsion pure = Mt.r Mt = G. .IGo et x = .L
IGo
Pour les calculs
de
résistance
N : effort normal en traction (Mpa) : contrainte normale (Mpa)
T : effort tranchant en cisaillement (Mpa) E :module d’Young (MPa)
S : section résistante en traction et cisaillement : déformation unitaire
Mfz : moment fléchissant en flexion (m.N) : contrainte de cisaillement (Mpa)
y : position du point M considéré dans la section droite G: module de Coulomb (MPa)
IGz : moment quadratique (mm4) : angle de cisaillement
Mt :moment de torsion (m.N)
r : position radiale du point M considéré dans la section l : allongement (mm)
droite y(x) : équation de la déformée
:angle de rotation unitaire (rad/mm)
IGo : moment quadratique polaire (mm 4)
x : angle de rotation (rad)
Quelques valeurs pour l’acier :
E = 2.105 Mpa, G = 8.104 Mpa, 200 Mpa < Re < 1400 Mpa, Rg ≈ 0,4 Re, = 7,8.103 kg.mm-3












