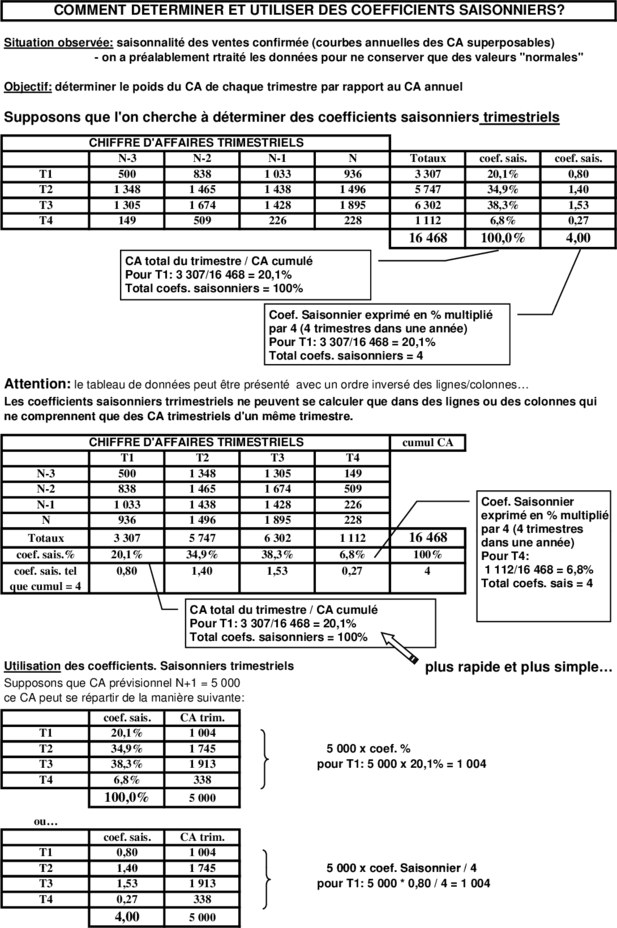
COMMENT DETERMINER ET UTILISER DES COEFFICIENTS SAISONNIERS?

Situation observée: saisonnalité des ventes confirmée (courbes annuelles des CA superposables)
- on a préalablement rtraité les données pour ne conserver que des valeurs "normales"

Objectif: déterminer le poids du CA de chaque trimestre par rapport au CA annuel

Supposons que l'on cherche à déterminer des coefficients saisonniers trimestriels
CHIFFRE D'AFFAIRES TRIMESTRIELS
N-3 N-2 N-1 N Totaux coef. sais. coef. sais.
T1 500 838 1 033 936 3 307 20,1% 0,80
T2 1 348 1 465 1 438 1 496 5 747 34,9% 1,40
T3 1 305 1 674 1 428 1 895 6 302 38,3% 1,53
T4 149 509 226 228 1 112 6,8% 0,27
16 468 100,0% 4,00
CA total du trimestre / CA cumulé
Pour T1: 3 307/16 468 = 20,1%
Total coefs. saisonniers = 100%

Coef. Saisonnier exprimé en % multiplié
par 4 (4 trimestres dans une année)
Pour T1: 3 307/16 468 = 20,1%
Total coefs. saisonniers = 4

Attention: le tableau de données peut être présenté avec un ordre inversé des lignes/colonnes…
Les coefficients saisonniers trrimestriels ne peuvent se calculer que dans des lignes ou des colonnes qui
ne comprennent que des CA trimestriels d'un même trimestre.

CHIFFRE D'AFFAIRES TRIMESTRIELS cumul CA
T1 T2 T3 T4
N-3 500 1 348 1 305 149
N-2 838 1 465 1 674 509
N-1 1 033 1 438 1 428 226 Coef. Saisonnier
N 936 1 496 1 895 228 exprimé en % multiplié
par 4 (4 trimestres
Totaux 3 307 5 747 6 302 1 112 16 468 dans une année)
coef. sais.% 20,1% 34,9% 38,3% 6,8% 100% Pour T4:
coef. sais. tel 0,80 1,40 1,53 0,27 4 1 112/16 468 = 6,8%
que cumul = 4 Total coefs. sais = 4

CA total du trimestre / CA cumulé
Pour T1: 3 307/16 468 = 20,1%
Total coefs. saisonniers = 100%

Utilisation des coefficients. Saisonniers trimestriels plus rapide et plus simple…
Supposons que CA prévisionnel N+1 = 5 000
ce CA peut se répartir de la manière suivante:
coef. sais. CA trim.
T1 20,1% 1 004
T2 34,9% 1 745 5 000 x coef. %
T3 38,3% 1 913 pour T1: 5 000 x 20,1% = 1 004
T4 6,8% 338
100,0% 5 000
ou…
coef. sais. CA trim.
T1 0,80 1 004
T2 1,40 1 745 5 000 x coef. Saisonnier / 4
T3 1,53 1 913 pour T1: 5 000 * 0,80 / 4 = 1 004
T4 0,27 338
4,00 5 000
Supposons que l'on cherche à déterminer des coefficients saisonniers mensuels

Détermination des coefficients saisonniers mensuels:


CHIFFRE D'AFFAIRES MENSUELS
Coef tel que
N-2 N-1 N Totaux Coef % cumul coef =
12
janvier 28 36 48 112 2,0% 0,24
février 58 64 82 204 3,7% 0,44
mars 64 78 88 230 4,2% 0,50
avril 98 112 139 349 6,3% 0,76
mai 222 258 298 778 14,1% 1,69
juin 304 345 402 1 051 19,1% 2,29
juillet 125 158 168 451 8,2% 0,98
août 88 99 125 312 5,7% 0,68
septembre 152 165 188 505 9,2% 1,10
octobre 164 184 218 566 10,3% 1,23
novembre 123 156 168 447 8,1% 0,97
décembre 162 168 182 512 9,3% 1,11
5 517 100,0% 12


= coef% x 12

plus rapide et plus simple…



Attention: le tableau de données peut être présenté avec un ordre inversé des lignes/colonnes…
Les coefficients saisonniers mensuels ne peuvent se calculer que dans des lignes ou des colonnes qui ne
comprennent que des CA mensuels d'un même mois.




Utilisation des coefficients saisonniers mensuels
Supposons que CA prévisionnel N+1 = 2 600
ce CA peut se répartir de la manière suivante: autre solution:

Coef % CA mensuel Coef tel que CA mensuel
= CA(N+1) cumul coef = CA(N+1)
x coef% = 12 x coef / 12
janvier 2,0% 53 janvier 0,24 53
février 3,7% 96 février 0,44 96
mars 4,2% 108 mars 0,50 108
avril 6,3% 164 avril 0,76 164
mai 14,1% 367 mai 1,69 367
juin 19,1% 495 juin 2,29 495
juillet 8,2% 213 juillet 0,98 213
août 5,7% 147 août 0,68 147
septembre 9,2% 238 septembre 1,10 238
octobre 10,3% 267 octobre 1,23 267
novembre 8,1% 211 novembre 0,97 211
décembre 9,3% 241 décembre 1,11 241
2 600 12,00 2 600
 METHODE DES MOINDRES CARRES
Limiter les calculs… et utiliser de manière optimale les ressources de sa calculatrice…
Méthode utile pour effectuer une prévision des ventes lorsque le CA progresse de manière linéaire

Objectifs :
déterminer s’il existe un lien de dépendance linéaire entre les 2 variables
o si ces variables sont le temps et le CA on vérifie donc si le CA progresse de manière linéaire
s’il est prouvé que le yi (souvent le CA) progresse de manière linéaire on pourra déterminer
l’équation de la droite d’ajustement y=ax+b
avec cette équation, on pourra effectuer des prévisions (donc calculer yi en fonction de xi…)(par
exemple : calculer le chiffre d’affaires des années futures en fonction du rang de ces années)

xi : variable explicative indépendante (xi est souvent le temps –rang de l’année par exemple, en
commençant par la plus ancienne-)
yi : variable expliquée par xi qui dépend de xi (yi est souvent le CA observé)

identifier la variable dépendante yi (pour une prévision des ventes, yi est toujours le CA)
construire le tableau de calculs statistiques sans effectuer les calculs…
saisir les couples de valeurs (xi ;yi) dans sa calculatrice (mode statistique/ série à 2 variables)
récupérer les ∑ à partir de la calculatrice et compléter la ligne « ∑» du tableau de calculs statistiques
présenter les formules de calcul des différents coefficients ; coefficients qui sont directement obtenus à
partir de la calculatrice
obtenir directement à partir de la calculatrice les prévisions de yi en fonction de xi

n = nombre de couples de valeurs (xi ;yi)
moyenne des xi : xm = ∑xi / n (
moyenne des yi : ym = ∑yi / n

r: coefficient de corrélation linéaire
corrélation linéaire vraiment justifiée si r<-0,97 ou si r>0,97 (r est toujours compris entre -1 et +1)

r= ∑xiyi –nxm. ym / racine [ (∑xi2- n.xm2). (∑yi2-...