Regardons un petit peu aujourd'hui l'algorithme qui vient de tomber hier dans l'épreuve de Maths commune aux séries ES Obligatoire et L Spécialité, pour les candidats passant les BAC ES et L 2013 dans les lycées français des Centres Etrangers
(Europe et Afrique).
Encore une fois, comme dans une écrasante majorité des cas au BAC, l'algorithme tombe dans le contexte d'un exercice sur les suites, mais petite originalité cette fois-ci dans un QCM sans justification ni pénalité en questions 4 et 5:
Question 4)Il s'agit donc d'interpréter ce que fait l'algorithme, en choisissant la bonne réponse:
- a) la valeur de U40000
- b) toutes les valeurs de U0 à UN
- c) le plus petit rang n pour lequel on a Un≤10000
- d) le nombre de termes inférieurs à 1200
L'algorithme de l'énoncé comporte l'affectation récurrente
"U prend la valeur 0,875U+1200" correspondant à la relation de récurrence donnée en introduction pour la suite: U
n+1=0,875U
n+1200.
De plus, on y trouve l'initialisation
"U prend la valeur 40000" qui correspond au terme initial U
0=40000.
Cet algorithme travaille donc sur la suite (U
n) de l'énoncé.
Donc, que fait-il avec?
L'algorithme est principalement constitué d'une boucle 'tant que'.
Sa condition de poursuite est U>10000, ce qui nous donne une condition d'arrêt terminant l'algorithme sur son contraire, U≤10000.
L'algorithme recherche donc le rang du premier terme de la suite (U
n) inférieur ou égal à 10000.
Réponse
c).
Question 5)On nous demande maintenant ce qu'affiche cet algorithme.
On peut tout simplement le programmer sur notre calculatrice et recopier la réponse.
Voici une adaptation possible de cette algorithme pout TI-76 et TI-82 à TI-84:
Si vous êtes équipé d'une Casio Graph ou Casio Prizm, en voici une autre:
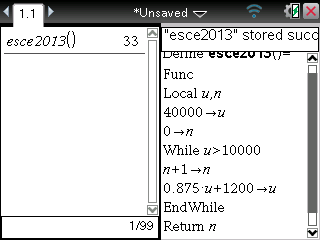
Enfin, pour une TI-Nspire ou TI-89/92/Voyage 200, voici une possibilité:
Dans tous les cas, la valeur affichée est donc 33 et la bonne réponse
a).
Mais si jamais vous n'étiez, malgré nos efforts, toujours pas à l'aise avec l'implémentation d'algorithmes sur votre calculatrice, il était parfaitement possible de résoudre autrement la question 5) à condition d'avoir compris la question 4)...
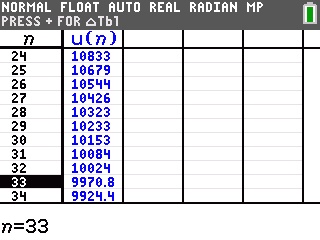
Il nous suffit en effet de demander à la calculatrice un tableau de valeurs de la suite, et de rechercher le rang du premier terme de valeur inférieure ou égale à 10000.
Prenons pour commencer une TI-82 à TI-84.
Passons donc en mode
'suite' ou
'sequence' en anglais -
La suite vous est donc définie par une relation de récurrence
Un+1=0,875Un+1200.
Mais la calculatrice ne vous permet pas de définir le terme de rang n+1 mais uniquement le terme de rang n.
Vous devez donc commencer par réécrire cette relation un rang en-dessous, c'est-à-dire en remplaçant tous les
'n' par des
'n-1'.
Cela nous donne
Un=0,875Un-1+1200Une fois cette relation établie, il vous suffit d'aller la saisir -
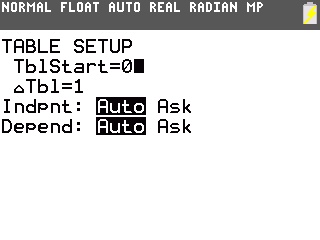
Selon l'état de votre calculatrice, il peut alors être nécessaire de modifier les paramètres du tableau de valeurs, à partir de 0 avec un pas de 1 dans le cas d'une suite -
Et vous pouvez enfin demander le tableau de valeurs -
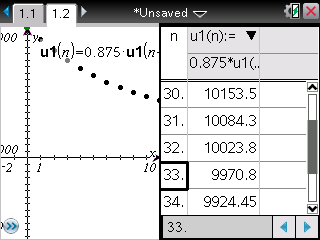
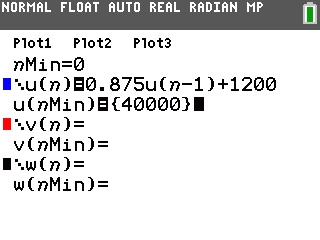
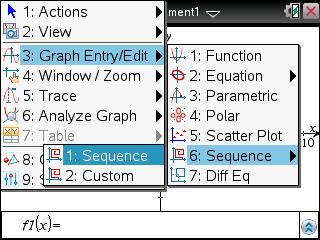
Sur TI-Nspire il vous faut utiliser la même relation.
Dans une application graphique, choisissez un entrée sous forme de suite -
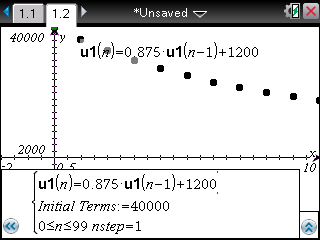
Saisissez alors la relation trouvée plus haut:
Et demandez le tableau de valeurs -
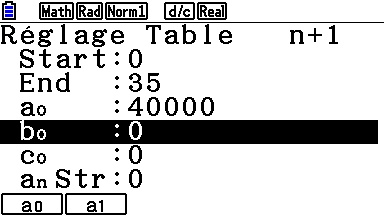
Si vous êtes munis d'une Casio Graph/Prizm, il suffit d'accéder à l'application
'Récurrence' pour y définir notre suite.
Ici, nul besoin de transformer l'expression contrairement aux calculatrices TI - on peut saisir directement celle de l'énoncé!
Mais il ne faut surtout pas oublier de préciser la valeur des termes initiaux, et cela se fait dans un autre écran accessible via le menu [SET]:
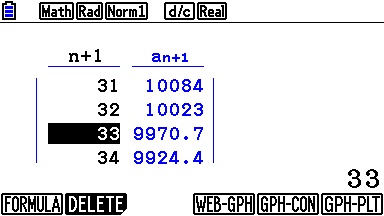
On y précise également les paramètres de notre tableau de valeurs, que voici enfin, une fois de plus cohérent avec l'affichage du programme!
La réponse est donc bien 33.
A bientôt! 
Liens:BAC ES 2013: Annales des sujets inédits et corrigésBAC L 2013: Annales des sujets inédits et corrigés
by 
