Regardons un petit peu ce soir l'algorithme qui vient de tomber dans l'épreuve de Maths commune aux série ES Obligatoire et L Spécialité, pour les candidats passant le BAC 2013 dans les lycées français du Liban.
Encore une fois, comme dans une majorité des cas au BAC, l'algorithme tombe dans le contexte de suites:
Question B)1)Une ville comportant initialement à l'année d'indice 0
(2012) 10000 habitants perd 10% de sa population chaque année
(c'est-à-dire qu'elle en garde 90%), mais gagne parallèlement 1200 personnes, soit 1,2 milliers.
On souhaite modéliser cette évolution à l'aide d'une suite u, donnant le nombre de milliers d'habitants.
La valeur initiale est donc u
0=10.
On traduit alors les deux autres informations de l'énoncé à l'aide de la relation de récurrence: u
n+1=0,9*u
n+1,2.
On remarque en effet que c'est exactement la suite étudiée en partie A de l'exercice.
Question B)2)On souhaite donc avoir un algorithme calculant les termes u
n de la suite.
L'énoncé, bien gentil, nous donne un algorithme à trou.
La variable a joue le rôle du terme de la suite: il est bien initialisé à 10.
La variable i varie de 1 à n et est donc un compteur permettant de calculer par récurrence les termes des rangs 1 à n.
La seule information de l'énoncé non présente dans cet algorithme est la relation de récurrence et on peut donc le compléter de la façon suivante:
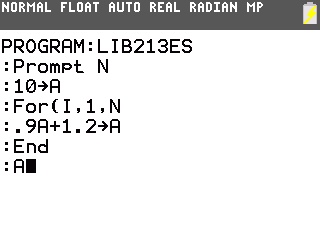
- Code: Select all
Choisir n
a prend la valeur 10
Pour i allant de 1 à n
a prend la valeur 0,9*a+1,2
FinPour
La calculatrice peut alors nous aider à vérifier si notre algorithme est correct.
Il suffit de le programmer et de comparer les valeurs affichées avec celles de la suite.
Voici le programme pour TI-82 à TI-84 et quelques valeurs:
Passons donc en mode
'suite' ou
'sequence' en anglais -
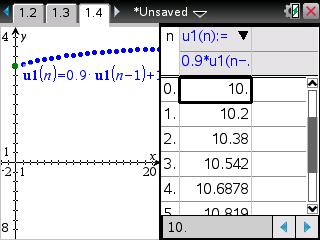
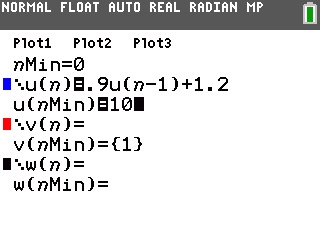
La suite vous est donc définie par une relation de récurrence
un+1=0,9*un+1,2.
La calculatrice ne vous permet pas de définir le terme de rang n+1 mais uniquement le terme de rang n.
Vous devez donc commencer par réécrire cette relation un rang en-dessous, c'est-à-dire en remplaçant tous les
'n' par des
'n-1'.
Cela nous donne
un=0,9*un-1+1,2Une fois cette relation établie, il vous suffit d'aller la saisir -
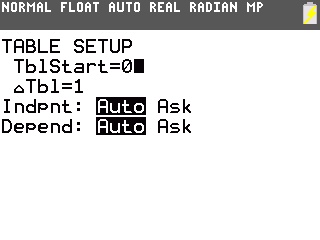
Selon l'état de votre calculatrice, il peut alors être nécessaire de modifier les paramètres du tableau de valeurs, à partir de 0 avec un pas de 1 dans le cas d'une suite -
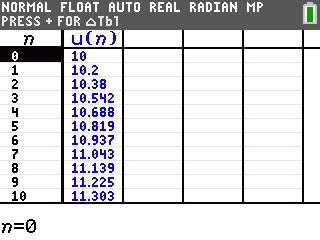
Et vous pouvez enfin demander le tableau de valeurs -
Notre programme et notre algorithme sont donc bons!
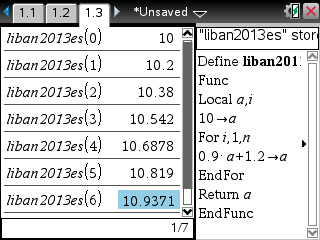
Sur TI-Nspire il vous faut utiliser la même relation.
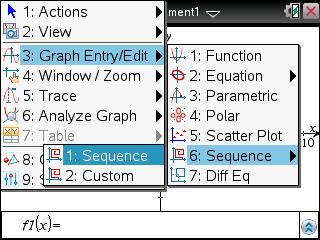
Dans une application graphique, choisissez un entrée sous forme de suite -
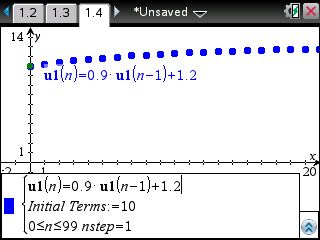
Saisissez alors la relation trouvée plus haut:
Et demandez le tableau de valeurs -
D'un autre côté, programmons l'algorithme et comparons les valeurs affichées:
Encore une fois c'est correct.
Si vous êtes munis d'une Casio Graph/Prizm, vous pouvez aussi réaliser la même chose en saisissant le programme suivant:
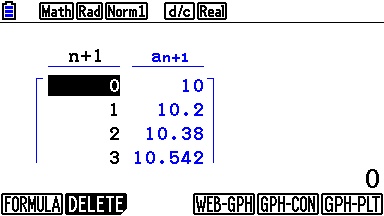
Il suffit maintenant d'accéder à l'application
'Récurrence' pour y définir notre suite.
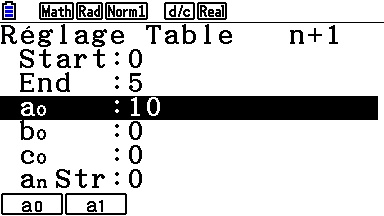
Ici, nul besoin de transformer l'expression - on peut saisir directement celle de l'énoncé!
Mais il ne faut surtout pas oublier de préciser la valeur des termes initiaux, et cela se fait dans un autre écran accessible via le menu [SET]:
On y précise également les paramètres de notre tableau de valeurs, que voici enfin, une fois de plus cohérent avec l'affichage du programme!
Liens:Annales des sujets inédits du BAC ES 2013 et corrigésAnnales des sujets inédits du BAC L 2013 et corrigés
by 
