[critor]

Depuis hier, les épreuves du nouveau BAC 2013 ont commencé pour les candidats des lycées français du Liban.

Ces sujets inédits sont d'une importance sans précédent cette année suite aux changements de programmes qui entraînent de nouvelles épreuves, dans le fond ou dans la forme.



Habituellement, les nouveaux sujets sont mis en ligne dès la fin des épreuves par le CDI du Collège Louise Wegmann , mais ce site n'est pour le moment pas à jour cette année.

En l'absence de source locale, des retards dans les disponibilités des sujets sont donc possibles, particulièrement dans les disciplines non scientifiques, mais nous les aurons!



Grâce à l'APMEP, voici déjà le sujet de Maths Spécialité pour les séries S!

Il y a bien évidemment un algorithme, et pour une fois en spécialité!

Avec le sujet tombé en Inde, c'est votre deuxième échantillon représentatif de ce que vous aurez bientôt au BAC 2013 - à regarder avec soin et dès maintenant!



Au menu:

• Exercice 1 (4 points): Un QCM sans justification et sans pénalité, et comme une majorité de QCM au BAC il porte sur la géométrie dans l'espace.
• Exercice 2 (5 points): Un problème de probabilités, touchant aux probabilités conditionnelles et aux lois normales qui sont une nouveauté cette année.
• Exercice 3 (6 points): Un exercice d'étude de fonction.
• Exercice 4 (5 points): Un exercice sur les suites et matrices qui sont une nouveauté cette année.

A bientôt!

Lien:
Annales des sujets inédits du BAC S 2013 et corrigés

[critor]

Intéressons-nous maintenant à l'algorithme qui est tombé en exercice 3 aux Olympiades Académiques 2013 de Première S dans l'Académie de Nice.

Il s'agit donc ici d'un problème d'éclairage.
Notons que là encore l'auteur du sujet fait plus de la traduction de langage de programmation que de l'algorithmie, notamment avec le test '==' pour l'égalité.



Question 6)a)
Commençons par la question 6.
L'algorithme donné nous construit un lotissement quadrillé 5x5, en codant 0 les zones d'ombre, 1 les zones éclairées, et 2 les maisons.
On nous demande un plan, et il nous suffit d'utiliser l'objet matrice (tableau de nombres vu en spécialité ES) de la calculatrice afin d'obtenir directement un schéma du lotissement.

Voici par exemple la construction d'une solution en utilisant les calculatrice TI-82 à TI-84:

Notre lotissement 5x5 est donc constitué de maisons en diagonale, et les terrains aux alentours ne sont pas du tout éclairés.

Nous obtenons heureusement le même résultat sur Casio Graph/Prizm...

... ou encore sur TI-Nspire:

Question 5)
Maintenant que nous avons vu la question 6, nous savons mieux comment manipuler et parcourir des matrices.
Nous pouvons donc répondre à la question 5, et produire un algorithme disant si le lotissement est bien éclairé ou pas.

Deux boucles 'pour' imbriquées sur les 5 lignes et les 5 colonnes permettent de parcourir toutes les cases du tableau.

Un lotissement est mal éclairé si l'on trouve une case non éclairée (valeur 0).
Comme il peut y avoir plusieurs cases non éclairées, afin d'éviter les affichages multiples il va nous falloir stocker le résultat à l'aide d'un drapeau et l'afficher en fin de boucle.

Code: Select all

e prend la valeur 1
Pour i de 1 à 5
   Pour j de 1 à 5
      Si T[i,j]=0 alors
         e prend la valeur 0
      FinSi
   FinPour
FinPour
Si e=0 alors
   Afficher "Le lotissement est mal éclairé"
Sinon
   Afficher "Le lotissement est bien éclairé"
FinSi

Codons et testons cela tout-de-suite sur TI-82 à TI-84, avec le lotissement de la question 6:

Sans surprise, ce lotissement est mal éclairé.

Voici maintenant le code pour Casio Graph/Prizm...

... et pour TI-Nspire/89/92/V200:

Lien:
Olympiades Acémiques 2013 de Première S (Académie de Nice)

[critor]

Voici aujourd'hui l'algorithme tombé en exercice 6 aux Olympiades Académiques de 1èreS dans l'Académie de Toulouse.

Il s'agit donc d'un partage d'une sphère selon de grands cercles (sections passant par son centre).
On suppose dans cet énoncé, que les grands cercles sont tous sécants deux à deux.



Question C)2)a):
On nous propose donc un algorithme permettant de déterminer le nombre de régions obtenues après quatre sections de la sphère.
Il nous suffit donc de programmer cet algorithme sur notre calculatrice graphique afin d'obtenir la réponse.

Voici sa traduction en un programme pour calculatrices TI-82 à TI-84:

L'exécution du programme nous donne alors la réponse, 14:

Si vous êtes équipés d'une calculatrice Casio Graph/Prizm, vous pouvez sans difficulté réaliser exactement la même chose:

Si vous êtes dotés d'une calculatrice TI-Nspire ou TI-89/92/V200, voici une solution:

Question C)2)b):
L'on nous demande maintenant d'expliquer pourquoi cet algorithme répond bien à la question.

Pour mieux comprendre ce qu'il fait, on pourrait construire la trace de l'algorithme, avec toutes les valeurs intermédiaires prises par la variable NbRegion à chaque passage dans la boucle.

La calculatrice peut nous donner directement cette trace avec l'ajout d'une simple instruction de sortie:

De l'initialisation à la sortie du programme, la variable N prend donc successivement les valeurs 2, 4, 8, 14.

C'est-à-dire que l'on ajoute successivement 2, 4 et 6.

En effet, la valeur initiale 2 est le nombre de régions déterminées par une section selon un grand cercle.

A la 2ème section, les grands cercles étant sécants deux à deux, les deux régions précédentes sont coupées en deux, ce qui nous rajoute 2 régions.

A la 3ème section, le nouveau grand cercle coupe les deux grands cercles précédents, ce qui rajoute 4 régions.

A la 4ème section, le nouveau grand cercle couple les trois grands grands cercles précédents, ce qui rajoute 6 régions.

Le même raisonnement peut être initié à partir d'une Casio Graph /Prizm ou d'une TI-Nspire/89/92/V200:

Lien:
Olympiades Académiques de 1ère 2013 (Académie de Toulouse)

[critor]

Tu peux trouver sur notre site de très nombreux corrigés d'exercices d'algorithmique d'examens et concours, appliqués aux calculatrices TI-z80, TI-Nspire et Casio Graph/Prizm.

Le site Planète-Casio avec Dark Storm entame lui une approche différente mais non moins intéressante. Il a déterminé 5 types d'algorithmes exigibles au lycée:

• Algorithme n°1 (Seconde): résolution d'équation par dichotomie
• Algorithme n°2 (Première S): liste de termes d’une suite définie par récurrence
• Algorithme n°3 (Première S): calcul d'un terme de rang donné d’une suite définie par récurrence
• Algorithme n°4 (Terminale S): dans le contexte d'une suite croissante tendant +∞, détermination d'un rang à partir duquel les termes sont strictement supérieurs à un réel A
• Algorithme n°5 (Terminale S): détermination d'un encadrement d’une intégrale pour une fonction monotone positive

La plupart des algorithmes que nous avons trouvés jusqu'à présent dans des sujets de BAC concernent effectivement les suites (algorithmes 2, 3 et 4).

Mais cette analyse a aussi ses limites, puisque plusieurs algorithmes tombés au BAC, que ce soit dans le contexte de suites ou non, ne relèvent pas de la classification ci-dessus.



Ce document n'en reste pas moins une très bonne base de travail, surtout que Dark Storm accompagne chaque algorithme d'une version TI et d'une version Casio!

La suite sur Planète-Casio

[critor]

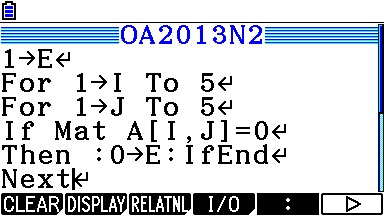
Ce soir, continuons de nous entraîner pour nos examens en regardant l'algorithme qui est tombé en exercice 3 aux Olympiades Académiques 2013 pour les Premières S de l'Académie de Montpellier:

Il y a ici une petite originalité, car en plus de l'algorithme il y a également une conjecture à réaliser sur calculatrice.





Question 1)a)
Nous devons donc exprimer l'aire du trapèze AECD.
La formule de l'aire du trapèze donne ici (AE+CD)*AD/2.
Mais en cas de trou de mémoire, on peut toujours répondre à la question en additionnant les aires des rectangle ABCD et triangle rectangle BCE.

CD=AB=2
AE=AB+BE=4+x
AD=BC=√(CE²-BE²)=√(1-x²)

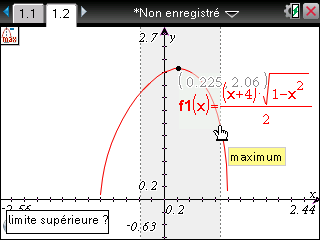
Nous obtenons donc f(x)=(x+4)√(1-x²)/2.



Question 1)b)
On nous demande maintenant de conjecturer la valeur du maximum de f à l'aide de la calculatrice.

Prenons donc notre calculatrice TI-82 à TI-84, et ouvrons l'éditeur pour y saisir notre fonction:

Nous pouvons alors demander sa courbe:

Notre calculatrice dispose d'un outil pour rechercher de façon précise le maximum - il nous suffit pour cela d'aller dans les outils d'analyse de courbe:

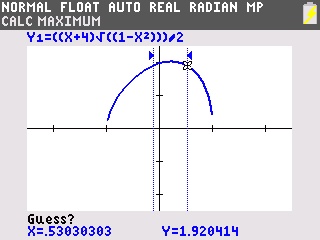
Nous spécifions alors graphiquement sur quel intervalle rechercher le maximum:

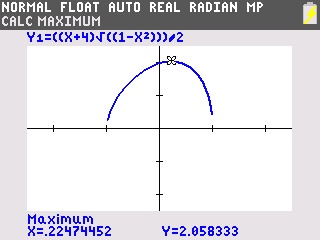
Et le voici enfin, maximum d'environ 2,1 pour x≈0,2:

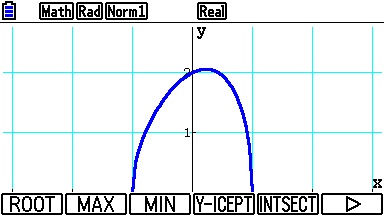
Si vous disposez d'une Casio Graph ou Casio Prizm, on procède selon les mêmes étapes.

On saisit l'expression en accédant à l'éditeur de fonctions depuis le menu principal:

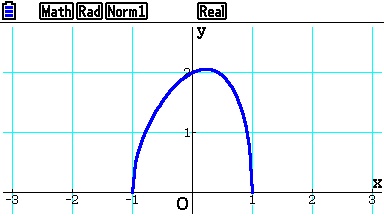
Avec [DRAW], on en demande la courbe:

En appuyant sur [SHIFT], nous obtenons alors un menu spécifique aux graphiques:

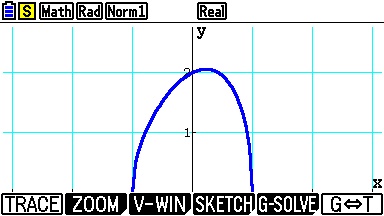
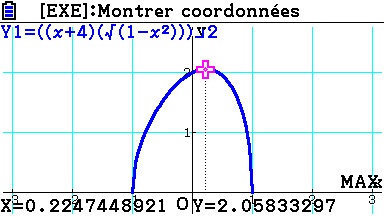
Nous y choisissons [G-SOLVE] (pour résolution graphique) et ensuite [MAX]:

Et voilà, même résultat - il n'y a pas d'intervalle à spécifier ici:

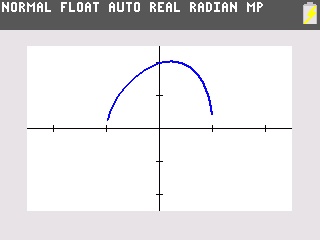
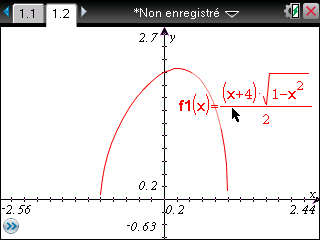
Sur TI-Nspire, nous saisirons l'expression dans l'application graphique:

Nous choisissons ensuite l'outil d'analyse de courbe approprié:

Après spécification graphique de l'intervalle de recherche, voici enfin à nouveau le même résultat:

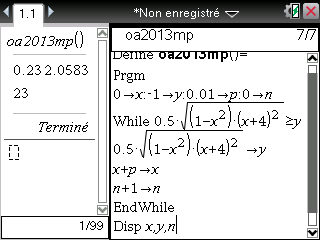
Question 2)a)
On nous donne donc un algorithme qui travaille sur l'expression 0,5√((1-x²)(x+4)²).
Mais remarquons que 0,5√((1-x²)(x+4)²)=0,5√((x+4)²)√(1-x²)=0,5(x+4)√(1-x²) car x+4≥ puisque x≥0 (x étant la longueur BE).
Cette expression revient dont finalement à f(x) et représente l'aire du trapèze.

Que fait donc l'algorithme là-dessus?
Il balaye les valeurs en partant de 0 par pas de 0,01 et continue tant que l'image est supérieure ou égale à la précédente.

En gros il recherche la plus grande image, soit le maximum.

De façon plus précise, comme on utilise un pas de 0,01 on peut dire que l'algorithme recherche l'abscisse du maximum à 10^-2 près.

Mais en fait, l'algorithme s'arrêtera uniquement lorsque l'on aura dépassé ce maximum en abscisse.
Contrairement à la question précédente, on pourrait donc dire que l'algorithme recherche ici à 10^-2 près par excès, la valeur de x correspondant au maximum.

Le maximum existant ici, la recherche se termine.







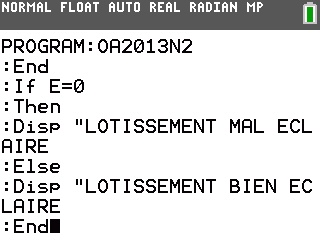
Question 2)b)

On nous demande enfin ce qu'affiche l'algorithme.
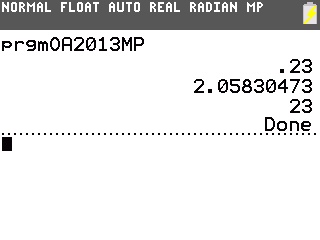
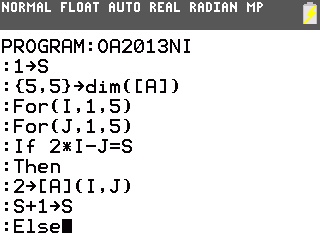
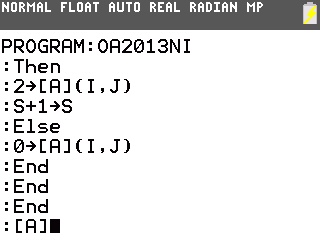
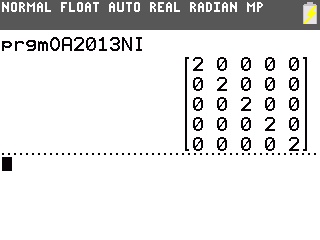
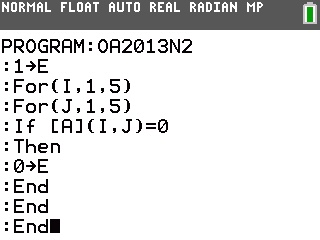
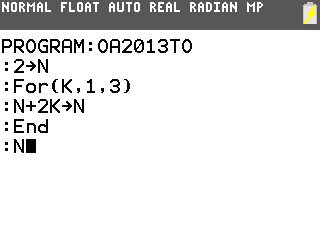
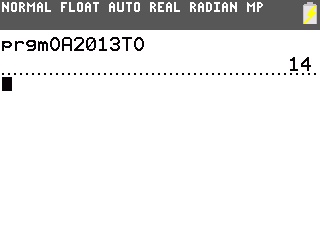
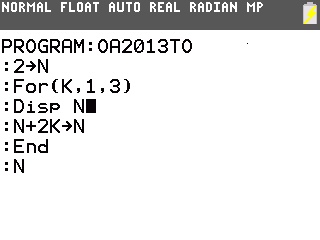
Il suffit pour cela de le programmer sur notre TI-82 à TI-84:

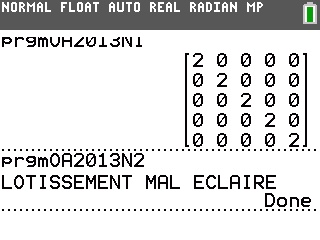
On obtient donc dans l'ordre 0,23, 2,058300473 et 23.

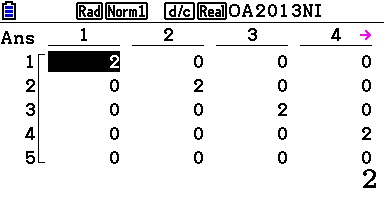
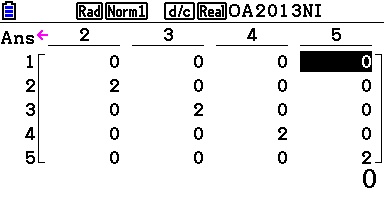
On peut également effectuer la programmation sur Casio Graph et Casio Prizm pour les mêmes résultats:

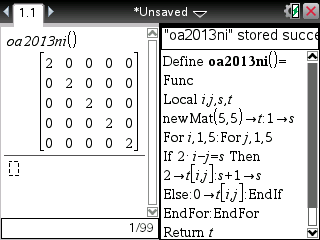
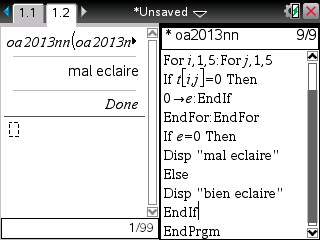
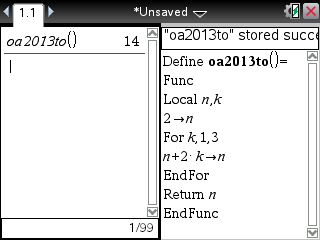
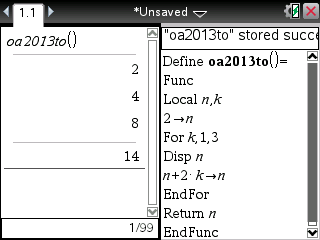
Ou encore sur TI-Nspire:

Lien:
Olympiades Académiques 2013 Premières S (Montpellier)