Concours de rentrée 2020 - défi Python du Léviathan

[critor]

Merci @NeOtuX.

Et pour le poster NumWorks, tu prends lequel ?

[NeOtuX]

Je passe mon tour pour le poster ; je n'ai plus de mur libre ! Et puis j'en ai eu un au défi précédent.

Merci !

[critor]

Ok, merci à toi.

[cent20]

C'est à moi non ?

[critor]

Bien, c'est donc à mon tour.

Je ne prends bien évidemment rien, mais je vais quand même expliquer ma modeste démarche.

Bien que familier du célèbre problème d'IA du monde du Wumpus dont est inspiré ce défi (si vous faites de l'IA dans l'enseignement supérieur vous en entendrez probablement parler), j'ai souhaité y aller très progressivement, afin de montrer la grande accessibilité du défi et inspirer les candidats.

Dans l'IA fournie exemple au taux de succès d'environ 7,3%, c'est le hasard qui prédomine. Quoi qu'il arrive, cette IA choisit toujours la corniche où elle va aller complètement au hasard en tirant au sort parmi les corniches voisines. Il lui arrive donc souvent de commettre des erreurs fatales.

J'a donc commencé par une IA n°1 surnommée "l'attaquante".

Elle est munie d'une mémoire des plus élémentaires, ne définissant même pas de liste ou autre objet composé.
A peine digne d'un poisson rouge, tout ce qu'elle fait, c'est de se souvenir :

• de la corniche précédente
• de si le Léviathan était détecté ou pas sur cette corniche précédente

Le Léviathan commençant à être détecté à 2 passerelles de distance, lorsque cette IA perçoit le Leviathan sur 2 corniches successives, elle décide de tirer sa flèche vers une corniche voisine au hasard (sauf celle dont elle vient).

Je catégorise cette IA en tant que réactive, son fonctionnement relevant plus du réflexe que de l'intelligence.

Mon IA n°1 permet déjà une amélioration significative du taux de succès par rapport à l'IA aléatoire fournie en exemple, dans les 8,5%.

Toutefois mon IA n°1 avait le défaut de souvent commettre des erreurs fatales.

J'ai donc continué avec une IA n°2 surnommée "la peureuse".

Pour corriger cela, je lui rajoute une mémoire de la corniche précédente (la corniche d'où elle vient). Lorsqu'elle sent un danger (puits ou Léviathan), elle retourne à la corniche dont elle vient, forcément sûre.

Cela suffit à réaliser un progrès extraordinaire, mon IA n°3 réussissant à sortir vivante du volcan dans les 22,9% des cas.

Mon IA n°2 avait toutefois le défaut d'être trop peureuse. Notamment, elle reculait dès qu'elle commençait à percevoir un danger, alors que dans le cas du Léviathan cela voulait dire à ce moment-là qu'il était à 2 passerelles de distance...

J'ai donc poursuivi avec une IA n°3, toujours réactive et donc simpliste, surnommée "la prudente".

Elle recule toujours si elle sent un puits, mais dans le cas du Léviathan elle ne recule que si elle le sent 2 fois de suite.

Léger progrès à 23,3% de succès, toujours mieux que rien.

Les IA précédentes avaient le défaut de continuer à se déplacer complètement au hasard, même après avoir trouvé la porte et la clé.

Il faudrait donc stocker l'environnement c'est-à-dire ici un graphe, c'est compliqué (niveau Terminale Spécialité NSI), allons-y doucement pour le moment.

Voici Mon IA n°4 affectueusement surnommée "le Petit Poucet".

Si elle trouve la porte avant la clé, à partir de ce moment-là elle retient le chemin emprunté.
Une fois la clé trouvée, elle revient alors tout simplement sur ses pas jusqu'à la porte.

Cette IA commence donc à avoir une connaissance, certes encore fort peu élaborée, de son environnement et on peut donc commencer à parler d'IA cognitive.
Mais elle ne fait appel à cette connaissance que dans certaines conditions (porte trouvée avant la clé) et en pratique il s'agit donc d'une IA hybride : à la fois réactive et cognitive.

Encore un léger progrès, à 24,5% de succès.

Afin d'être sûre de retrouver la sortie sans danger une fois la clé trouvée, le Petit Poucet revenait bêtement sur ses pas jusqu'à la porte.

Or les déplacements lors de l'exploration étant encore aléatoires, il pouvait donc y avoir plein de circuits inutiles lors du trajet retour.

Voici donc maintenant ma nouvelle amélioration avec l'IA n°5 alias "le Grand Poucet".

"Le Grand Poucet" a grandi et a maintenant appris à compter. Une fois la porte trouvée, il sème sur chaque corniche visitée des cailloux qu'il numérote par ordre croissant. Si la corniche comporte déjà un caillou il le laisse et n'en rajoute pas.

Lors du trajet retour une fois la clé trouvée, il retourne toujours vers la corniche indiquée par le plus petit numéro de caillou, c'est-à-dire la corniche la plus anciennement atteinte après passage par la porte.

En fait, on parcourt un arbre inclus dans le le graphe représentant notre trajet. Il est à noter que cet algo ne fournit pas forcément le plus court chemin connu, mais simplement un chemin sans circuit. Voici un contre-exemple : prenons la liste de visites successives {1, 2, 3, 1, 3, 4}, avec la porte en 1 et la clé en 4. Notre nouvelle IA va revenir en effectuant le chemin {4,3,2,1}, ce qui est déjà mieux que {4, 3, 1, 3, 2, 1} avec l'IA précédente. Toutefois le plus court chemin serait {4,3,1}.

Mais alors, pourquoi avoir implémenté cette IA ? Il s'agissait tout simplement montrer que l’on peut obtenir une IA d'une bien meilleure efficacité, sans avoir pour autant encore à stocker en mémoire tout l’environnement et à faire tourner de gros algos de recherche de plus court chemin dessus. Cette IA offre donc un bon compromis entre performances (une fois la porte puis la clé trouvées) et espace mémoire utilisé, particulièrement bienvenu sur NumWorks et TI-83 Premium CE.

Et effectivement, encore une progression notable à 25,1% de succès.

Mes IA précédentes avaient certes l'avantage de reculer en cas de danger détecté, évitant ainsi des erreurs fatales.

Mes sur certains graphes, cette stratégie d'évitement les confinait à explorer un sous-graphe, pas toujours suffisant pour réussir à s'échapper.
Elles étaient ainsi condamnées à erreur éternellement, ou plus précisément jusqu'au time out que nous avions prévu pour ces cas-là.

Sans renoncer à cette précaution salutaire, voici maintenant mon IA n°6, alias "la Kamikaze".

Elle commence à avoir une mémoire un peu plus élaborée de son environnement, mais toujours partielle. A chaque coup elle maintient à jour 2 listes :

• liste des corniches déjà visitées
• liste des corniches restant à visiter

Ne sont rajoutées dans cette dernière liste que les seules corniches détectées comme sûres.

Et donc nuance, en cas de danger détecté, cette IA ne recule que si il lui reste encore des corniches garanties comme sûres à visiter.
Dans la négative, elle tente le tout pour le tout... kamikaze !

Pas de nette amélioration ici, on reste dans les 25,1% de succès, il est temps de sortir les grands moyens...

La clé pour progresser vers des pourcentages de réussite extraordinaires, c'est de stocker l'intégralité du monde exploré dans la mémoire de l'IA, c'est-à-dire un objet de type graphe qui devrait parler aux spécialistes NSI.
À chaque nouvelle information, il est alors très facile d'effectuer des déductions positives ou négatives sur les corniches voisines, et voisines de voisines.
Un peu de logique permettra même d'aller au-delà.

Voici donc ma nouvelle IA, surnommée la 4x4.

Elle stocke tout l'environnement connue, et à chaque coup choisit un chemin possible répondant dans l'ordre aux stratégies suivantes :

1. si on a ramassé la clé et que l'on a trouvé ou déduit la position de la porte, aller prendre la porte
2. si on a déduit la position de la clé, aller ramasser la clé
3. aller explorer des corniches marquées comme ayant peut-être la clé
4. aller explorer des corniches non visitées

A chaque coup, elle envisage de plus cette série de stratégies au pire 4 fois, selon 4 niveaux de risque successifs :

• 0 : chemin passant uniquement par des corniches sûres
• 1 : si on a encore notre flèche, chemin pouvant passer par des corniches marquées comme abritant peut-être le Léviathan
• 2 : chemin pouvant passer par des corniches abritant des chauves-souris
• 3 : chemin pouvant passer par des corniches dissimulant peut-être un puits ou le Léviathan

Comme tu le vois, stocker l'environnement implique ici de pouvoir réfléchir dessus, et donc trouver un chemin vers ce que l'on y cherche (le Léviathan, la clé, la porte...).
Il faut donc une fonction de recherche de chemin au sein d'un graphe, et mine de rien c'est l'une des fonctions les plus importantes de notre IA, conditionnant directement non seulement ses performances mais également son efficacité.

De préférence les chemins choisis devront être les plus courts, histoire de minimiser le nombre de coups moyen qui compte au score.

Les Terminales ES Spécialité Maths connaissaient l'algorithme de Dijkstra. Mais ici pas besoin de sortir l'artillerie lourde, nous sommes sur un cas beaucoup plus simple : comme le score compte le nombre de coups, c'est comme si sur notre graphe toutes toutes les corniches étaient à égale distance les unes des autres.
Il s'agit donc d'un graphe non pondéré et non orienté.

L'exploration d'un graphe à partir de la corniche courante et à la recherche d'une cible vers laquelle on souhaite construire le chemin le plus court peut se faire au choix :

• en profondeur (DFS : Depth-First Search) :
  A chaque étape, on rajoute les corniches voisines puis se rend sur une corniche voisine non déjà explorée. Si il n'y a plus de corniche voisine inexplorée, on revient en arrière pour retenter.
  Ce parcours explore à fond (jusqu'à un cul de sac ou jusqu'à ne plus atteindre que des corniches déjà explorées) tous les chemins ouverts par une voisine de notre position courante , avant de passer à une autre voisine.
  Algorithmiquement il s'implémente avec une pile LIFO (Last In First Out), les derniers voisins rajoutés étant les premiers à être explorés.
• en largeur (BFS : Breadth-First-Search) :
  Cet algorithme diffère du précédent dans le fait qu'il explore en parallèle l'intégralité des voisins directs d'une corniche.
  C'est-à-dire qu'il teste dabord tous les chemins de longueur 1 à partir de la corniche courante, puis tous les chemins de longueur 2, de longueur 3, etc.
  Algorithmiquement il s'implémente avec une file FIFO (First In First Out), les derniers voisins rajoutés étant les derniers à être explorés.

Dans le cas qui nous intéresse ici, trouver le plus court chemin sur un graphe non pondéré, je choisis d'implémenter un algorithme de type BFS.
En effet comme il explore en parallèle les chemins possibles de plus en plus longs à partir de la corniche courante, un gros avantage est que lorsqu'il trouvera un chemin atteignant la cible ce sera forcément le plus court. Pas besoin donc de continuer à explorer.

Ces algorithmes s'écrivent facilement en récursif, c'est-à-dire avec une fonction qui se rappelle elle-même pour chaque nouvelle corniche à explorer.
Toutefois avec des corniches voisines qui ont elles-mêmes des voisines, la progression de la consommation de ressources (mémoire, temps processeur) au cours de l'exploration est exponentielle.

Je fais donc un effort pour coder l'algorithme BFS en itératif, mais voilà je suis récompensé, une fonction qui me donne le plus court chemin vers ma destination de façon fiable et rapide.



Passons maintenant aux déductions.

Les chauves-souris n'étant ressenties qu'une fois arrivé sur la corniche en question, c'est trivial.

Pour la porte c'est pareil, mais comme il n'y en a qu'une on peut avoir une déduction globale : si toutes les corniches ont été explorées sauf une et que l'on a pas encore trouvé la porte, alors elle est forcément sur cette dernière.

Pour les puits, je fais des déductions locales à la fois positives et négatives.
Les puits étant ressentis à 1 passerelle de distance :

• j'initialise toutes les corniches voisines à un état dit inconnu (pas d'information)
• si je ne perçois pas de puits, je marque que toutes les corniches voisines n'ont pas de puits
• si je perçois un puits, pour toutes les corniches voisines qui sont encore à l'état inconnu, je marque qu'elles ont peut-être un puits

Une corniche peut alors être déduite comme dissimulant un puits si :

• elle a été marquée comme dissimulant peut-être un puits
• et que toutes ses voisines n'ont pas de puits
• et que toutes les voisines de ses voisines n'ont pas de puits

Pour la clé elle aussi ressentie à 1 passerelle de distance même principe. Mais comme en plus il n'y en a qu'une, on peut combiner déductions locales et globale.

Pour le Léviathan les déductions locales positives sont plus complexes puisque ressenti à 2 passerelles de distance.
Pour l'instant je me contente de marquer qu'il n'est pas sur les corniches voisines :

• bien évidemment lorsque je ne le perçois pas
• mais également lorsque je le perçois alors qu'il n'était pas perçu sur la corniche précédente - c'est en effet qu'il est à ce moment-là obligatoirement à 2 passerelles de distance, et donc pas sur une corniche voisine

Les déductions positives donnent également de possibles nouvelles informations alors marquées :

• une corniche avec puits ne peut pas avoir la clé
• la corniche de la clé ne peut pas dissimuler un puits

Voici maintenant le schéma du raisonnement de cette IA, pleinement cognitive cette fois-ci :

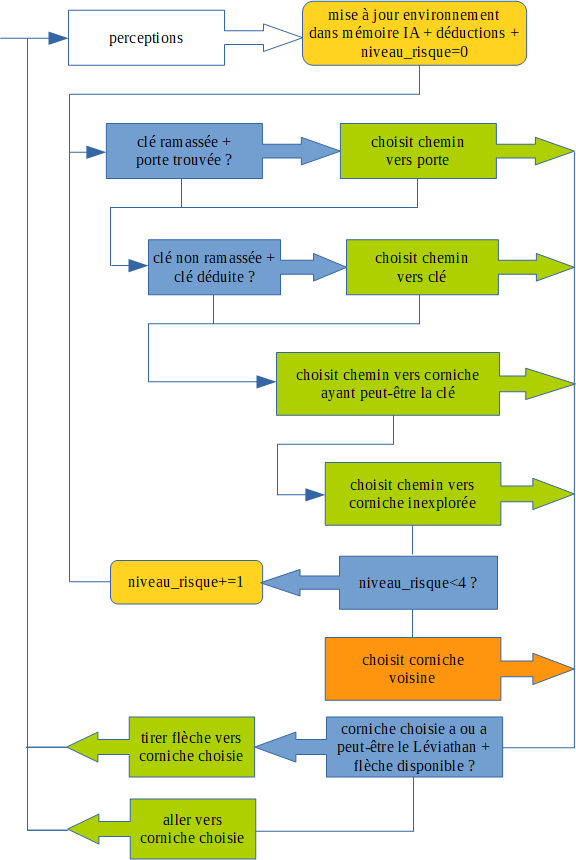
Une amélioration extraordinaire, on passe à 75% de succès !

Petit résumé de mes tentatives :

	Type	Déplacement normal	Déplacement retour (clé trouvée après porte)	Déplacement en cas de danger	Déplacement en cas de blocage	Condition de tir	Succès
Exemple fourni	aléatoire	corniche voisine au hasard				jamais	≈7,3%
n°1 "l'attaquante"	réactive	corniche voisine au hasard				corniche voisine au hasard quand Léviathan détecté 2 fois de suite	≈8,5%
n°2 "la peureuse"	réactive	corniche voisine au hasard		corniche précédente si puits ou Léviathan détecté		corniche voisine au hasard quand Léviathan détecté 2 fois de suite	≈22,9%
n°3 "la prudente"	réactive	corniche voisine au hasard		corniche précédente si puits détecté ou 2 fois de suite Léviathan détecté		corniche voisine au hasard quand Léviathan détecté 2 fois de suite	≈23,3%
n°4 "le Petit Poucet"	réactive + cognitive	corniche voisine au hasard	corniches précédentes	corniche précédente si puits détecté ou 2 fois de suite Léviathan détecté		corniche voisine au hasard quand Léviathan détecté 2 fois de suite	≈24,5%
n°5 "le Grand Poucet"	réactive + cognitive	corniche voisine au hasard	corniche voisine la plus anciennement atteinte après découverte porte	corniche précédente si puits détecté ou 2 fois de suite Léviathan détecté		corniche voisine au hasard quand Léviathan détecté 2 fois de suite	≈25,1%
n°6 "la Kamikaze"	réactive + cognitive	corniche voisine au hasard	corniche voisine la plus anciennement atteinte après découverte porte	corniche précédente si puits détecté ou 2 fois de suite Léviathan détecté	corniche voisine au hasard	corniche voisine au hasard quand Léviathan détecté 2 fois de suite	≈25,1%
n°7 "la 4x4"	cognitive	plus court chemin vers clé si déduite et non ramassée ou corniche inexplorée	plus court chemin vers la porte	plus court chemin vers clé si déduite et non ramassée ou corniche inexplorée	plus court chemin vers clé si déduite et non ramassée ou corniche inexplorée	Léviathan déduit ou Léviathan possible et plus rien à explorer	≈75%

Cette dernière IA est encore loin d'être parfaite, et j'avais des pistes pour aller plus loin.

Il m'aurait fallu travailler les déductions du Léviathan.
J'avais également pour projet de recoder intégralement l'environnement et ses règles logiques en Prolog, appelables en Python par l'intermédiaire du module pyswip.
Il suffit en effet d'y coder les simples règles élémentaires, pour que l'environnement Prolog se débrouille afin de les itérer sur l'intégralité de l'environnement pour en tirer les déductions positives et négatives possibles.

Même le plus court chemin pourrait être codé en Prolog, le script Python ne traitant alors plus du tout du graphe.

J'ai toutefois manqué de temps avec l'évaluation des participations qui se sont multipliées vers la fin du défi.

Un défi très riche, j'espère pouvoir aller plus loin une prochaine fois.

[critor]

Donc oui @cent20, maintenant c'est ton tour.

Félicitations pour ton classement parmi les meilleurs à ce défi !

Et merci pour ton explication.

Que nous prends-tu ?

• 1 lot Capricorne ♑ : 1 calculatrice Casio Graph 90+E + 1 pack de goodies Casio + 1 goodie Xcas + 1 pack de goodies TI-Planet & Planète Casio
• 2 lots Bélier ♈ : 1 solution d'émulation Casio au choix + 1 catalogue de produits Casio au choix + 1 pack de goodies Casio + 1 goodie Xcas + 1 pack de goodies TI-Planet & Planète Casio
  
  Show/Hide spoilerAfficher/Masquer le spoiler

  Détail des solutions d'émulation Casio au choix :
  

  • clé USB 8 Go d'émulation permanente au choix, à jour avec 3 émulateurs pour Windows : fx-92+ Spéciale Collège + Graph 35+E II 3.30 + Graph 90+E 3.40
    
    • clé à capuchon Transcend 2019 (7,5 Go de capacité réelle)
    • clé monolithique EMTEC 2020 (7,7 Go de capacité réelle)
  • licence 3 ans utilisable pour l'installation de tout ou partie des logiciels d'émulation suivants :
    
    • fx-CP400 Manager pour Windows / Mac
    • fx-CG500 Manager pour Windows / Mac
  
  
  
  
  
  
• Lot Serpentaire ⛎ : 1 goodie HP au choix + 1 goodie Xcas + 1 pack de goodies TI-Planète-Casio
  
  Show/Hide spoilerAfficher/Masquer le spoiler

  Poster HP : format 59,2×40 cm².
  
  
  
  
  
  
• 3 lots Balance ♎ : 1 couvercle NumWorks au choix + 1 autocollant NumWorks + 1 enveloppe NumWorks ou carte postale NumWorks ou carte de visite-énigme NumWorks au choix + 1 pack de goodies NumWorks + 1 goodie Xcas + 1 pack de goodies TI-Planet & Planète Casio
  
  Show/Hide spoilerAfficher/Masquer le spoiler

  Couvercle NumWorks au nouveau format N0110 protégeant mieux l'écran contre les rayures, mais restant parfaitement utilisable sur l'ancien modèle N0100.
  
  
  
  
  
  
• Lot Taureau ♉ : 1 calculatrice TI-Nspire CX II-T CAS + 1 licence logiciel TI-Nspire CAS élève + 1 pack de goodies TI + 1 goodie Xcas + 1 pack de goodies TI-Planète-Casio
• Lot Lion ♌ : 1 calculatrice TI-Nspire CX II-T + 1 licence logiciel TI-Nspire élève + 1 pack de goodies TI + 1 goodie Xcas + 1 pack de goodies TI-Planète-Casio
• Lot Gémeaux ♊ : 1 calculatrice TI-83 Premium CE Edition Python au choix + 1 adaptateur USB + 1 clavier USB dédié + 1 chargeur mural au choix + 1 housse Wyngs bleue ou film de protection écran Wyngs + 1 pack de goodies TI + 1 pack de goodies TI-Planète-Casio
• Lot Verseau ♒ : 1 calculatrice TI-83 Premium CE Edition Python + 1 gravure texte laser au choix + 1 adaptateur USB + 1 clavier USB dédié + 1 chargeur mural + 1 housse Wyngs au choix + 1 film de protection écran Wyngs dédiés + 1 extension de garantie 6 ans Calcuso + 1 pack de goodies TI + 1 pack de goodies TI-Planète-Casio
  
  Show/Hide spoilerAfficher/Masquer le spoiler

  Détail des calculatrices TI-Nspire CX II-T CAS au choix :
  

  • TI-Nspire CX II-T CAS sous blister version B
  • TI-Nspire CX II-T CAS sous blister version B avec autocollant sceau Comenius Edumedia 2019

  
  Détail des calculatrices TI-83 Premium CE Edition Python au choix pour le lot Gémeaux ♊ :
  

  • TI-83 Premium CE Edition Python sous blister version E
  • TI-83 Premium CE Edition Python sous blister version E avec autocollant masquant sceau Approuvé par les familles 2019

  
  La gravure au laser de la TI-83 Premium CE Edition Python du lot Verseau ♒ est effectuée par Calcuso. Le texte souhaité est à nous communiquer par le gagnant choisissant ce lot, dans la limite de 22 caractères et sans caractères spéciaux.
  
  
  [

Détail des packs de goodies communs accompagnant les lots :

Casio NumWorks TI Xcas TI-Planète-Casio

• 1 stylo Casio au choix
• 1 clé USB Casio au choix :
  
  • clé USB Casio fx-CP400+E - 4,019 Go
  • clé USB Casio - 4,018 Go
• 1 batterie USB Casio
• 1 histoire intégrale imprimée du manga Casio Academy - ClassWiz Edition - Function Hero - épisode 1, 2 ou 3 au choix - 5 pages ci-dessous + page de fin secrète :
  
  • Episode 0 : Kaito (pour référence)
  • Episode 1 : Takuma
  • Episode 2 : Emi
  • Episode 3 : Azusa
  

• 1 manuel NumWorks N0100
• 1 cahier d'activités NumWorks SNT 2nde
• 1 sac NumWorks au choix (N0100 versions 1.0-1.5, N0100 versions 1.6+, ou N0110)
• 1 cahier NumWorks
• 1 poster NumWorks au choix format A2 (42×59,4 cm²) :
  
  • NumWorks N0100 : Eduscol / Ministère de l'Education Nationale - roulé - brillant
  • NumWorks N0100 : Eduscol / Ministère de l'Education Nationale - roulé - mat
  • NumWorks N0110 : Comprendre le monde devient un jeu - plié
• 1 stylo NumWorks

• 1 stylo TI au choix
• 1 porte-documents TI
• 1 poster TI plié au choix :
  
  • format ANSI-D (55,9×86,4 cm²) : TI-73 Explorer
  • format A1 (59,4×84,1 cm²) : TI-89 Titanium
  • format 55,75×83,5 cm² : TI-Nspire CX, TI-Nspire CX CAS
• 1 clé USB TI au choix :
  
  • clé USB T3 France bleue - 2 Go de capacité nominale
  • clé USB TI-Primaire Plus - 4,01759 Go de capacité réelle
  • clé USB TI-Innovator Rover - 4,01813 Go de capacité réelle
  • clé USB TI-83 Premium CE avec lanière - 4,01811 Go de capacité réelle
  • clé USB TI-83 Premium CE avec chaînette - 4,01811 Go de capacité réelle
  • clé USB TI rouge - 1 Mo de capacité nominale (promotion TI-Primaire Plus défectueuse)
• 1 autocollant TI ou décalcomanie TI ou pochette CD TI ou lunettes TI au choix
• 1 cahier TI-83 Premium CE au choix

Aperçus de quelques cahiers d'activités TI-83 Premium CE Python au choix:

• Eyrolles : TI-83 Premium CE Edition Python - 2^nde Générale + Technique - Mathématiques extrait ou intégral au choix
• Eyrolles : TI-83 Premium CE Edition Python - Mathématiques + Physique-Chimie
• Eyrolles : TI-83 Premium CE Edition Python - SNT
• TI-83 Premium CE Edition Python - 2^nde Professionnelle - Mathématiques + Physique-Chimie
• Eyrolles : TI-83 Premium CE - BAC Pro - Mathématiques + Physique-Chimie
• Eyrolles : TI-83 Premium CE - 2^nde - ICN
• Eyrolles : TI-83 Premium CE - 2^nde + 1^ère - ICN

1 autocollant Xcas

• 1 autocollant TI-Planet au choix
• 1 autocollant Planète Casio
• 1 compte premium TI-Planet

[cent20]

Ton explication ... un vrai roman.

Il faut reconnaître que tes premières IA, commentées dans les tableaux sur les premières pages ici, là ou encore là ont été une source d'idée; et inspirante.

Ce défi était passionnant, mais pas facile à prendre en main, et sans le script d'évaluation graphique de LeGmask et et le script de benchmark de Citorva j'aurais été en difficulté pour progresser, c'est à dire complétement aveugle.

A mon grand regret, mes spé NSI ne l'ont pas vraiment cherché, je leur ai fait pourtant deux démos en classe à l'aide de la compilation des scripts précédemment évoqués publiés ici , mais la marche était trop haute pour eux. Deux seulement ont envoyés leurs scripts, et quand il me les ont montré j'ai compris qu'ils pataugeaient dans la semoule...

Pour le lot, dans le lot balance, j'hésite entre les deux couvercles et je ne sais pas lequel choisir :



Que me conseilles-tu Critor ?
Lequel est le couvercle collector en édition très limité ?
Lequel pourra se trouver facilement plus tard ?

[critor]

Pour le lot, dans le lot balance, j'hésite entre les deux couvercles et je ne sais pas lequel choisir :



Que me conseilles-tu Critor ?
Lequel est le couvercle collector en édition très limité ?
Lequel pourra se trouver facilement plus tard ?

Les deux sont censés être des éditions limitées gagnées en 12 exemples sur les RS à 1 mois d'intervalle, donc sur la valeur/rareté a priori pas de différence.

J'ai une préférence purement culturelle pour celui de droite.

Sinon il te suffit juste de demander à ta calculatrice, quand même la principale intéressée, ce qu'elle préfère.
Pour cela :

• tu sors ta NumWorks
• tu l'allumes
• tu vas dans l'application Python
• tu lances la console
• tu tapes from random import *
• tu tapes randint(10,11)

Elle te répondra 10 si elle préfère comme moi l'édition limitée d'Octobre 2020, ou bien 11 si elle préfère l'édition limitée de Novembre 2020.

Tiens-nous au courant de son choix stp, merci.

[cent20]

Un tirage aléatoire de 666 fois la séquence

Code: Select all

randint(10,11)

m'a donné 333 fois la réponse 10 et 333 fois la réponse 11.

Cela m'a laissé dans l'expectative...

Ma fille préfère le roi et la reine, donc cela sera mon choix final.

Ainsi, mon choix s'arrête sur le lot balance, avec le couvercle "Roi / Reine", l'autocollant, la carte de visite-énigme NumWorks.

Dans le pack de goodies NumWorks :
- Le sac qui est visuellement le plus chargé
- le poster d'un certain Xavier A., j'espère que tu pourras lui demander de me le dédicacer si tu le croises.

Dans le pack de TI-Planète-Casio, l'autocollant simple, sans le symbole VIP

Merci à tous pour ce défi, cela fut très disputé.
L'année prochaine, il faudra me laisser gagner la N0200 !

[critor]

Merci.

Je suis sincèrement désolé, le poster demandé est épuisé, il ne m'en reste même plus pour moi.
Après je peux toujours te dédicacer autre chose.

Ce qui est encore disponible est normalement à jour dans le dernier post de ce fil :
viewtopic.php?f=49&t=24387&p=258403#p258399