Parmi eux, ceux qui ont passé le BAC S en 2012 se sont retrouvé avec une question d'algorithmique en mathématique, comme la quasi totalité des candidats de par le monde car dans la 15aine de sujets prévus pour les différents centres d'examens en métropole et à l'étranger, tous sauf un comportaient une ou deux questions d'algorithmique.
L'algorithmique est donc à la mode en ce moment au BAC S, comme les QCM et ROC l'ont été en leur temps et tombent désormais de façon beaucoup moins intensive.
Curieusement, ceux qui ont passé le BAC ES en 2012 et avaient pourtant bien eu la même préparation en Seconde et le programme transitoire de Première-Terminale mettant l'accent sur l'algorithmique ont échappé à l'évaluation de ces compétences.
Enfin non... presque tous!

Car les tous derniers sujets du BAC 2012 qui viennent de tomber changent la donne: les candidats au BAC ES en Nouvelle Calédonie ont eu droit à un algorithme.
Dans le contexte actuel, ça ne m'étonnerait pas du tout que le nombre de sujets de maths avec des algorithmes pour le BAC ES 2013 soit bien plus important.
Et ça donne aussi une tendance pour les futurs sujets de maths du BAC technologique 2014, puisque les nouveaux programmes appliqués depuis la rentrée 2012 en Première mettent là encore l'accent sur les algorithmes comme compétence transversale à mettre en oeuvre dans tous les chapitres.
Bref, même si vous n'êtes pas en série S, vous n'avez plus la garantie d'échapper aux algorithmes - alors regardons de suite ce que donne ce tout premier algorithme 'non-S'.
Il s'agit donc ici de l'exercice 3, dont la partie B porte presque entièrement sur l'algorithme:

L'algorithme demande une valeur p à l'utilisateur, commence à x=3 et recherche avec un pas de 1 la 1ère valeur de x telle que f(x)≥p (le contraire de la condition de poursuite de la boucle 'tant que': f(x)<p).
L'énoncé nous fait cadeau d'un résultat: si on saisit 0,9 comme valeur de p, l'algorithme répond 249. Il nous est juste demandé d'interpréter.
C'est là qu'il faut comprendre le texte introduisant la partie B: la fonction f donne la proportion de billets vendus en fonction du nombre de jours écoulés.
C'est donc après 249 jours qu'il y aura au moins 90% de billets vendus.
La dernière question nous demande alors ce que répond l'algorithme si l'on saisit 0,5 comme valeur de p.
L'algorithme ici n'est pas du tout prévu pour être programmé de façon simple sur une caculatrice, de par l'utilisation d'une fonction externe non définie dans l'algorithme d'une part, et de par l'affichage de longs messages dépassant la largeur de l'écran d'autre part.
En fait il n'est nul besoin d'une calculatrice à ce niveau là de l'exercice: appliquer l'algorithme revient à chercher un arrondi à l'unité par excès d'un nombre α tel que f(α)=0,5.
Et comme par hasard, il a déjà été répondu à cette question en A.4). Il suffit donc de recopier ce résultat.

Maintenant, pour les passionnés qui tiendraient à tout prix à implémenter ceci sur leurs calculatrices, voici quelques propositions possibles. Dans tous les cas, nous définissons une fonction externe que nous utilisons ensuite dans le programme.
Voici pour les graphiques TI-73 à TI-84:
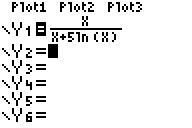
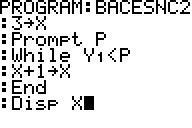
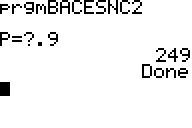
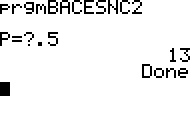
On confirme bien le résultat de 249 pour p=0,9 donné par l'énoncé et pour p=0,5 on obtient 13 jours.
Voici maintenant pour calculatrice TI-Nspire selon la même méthode:
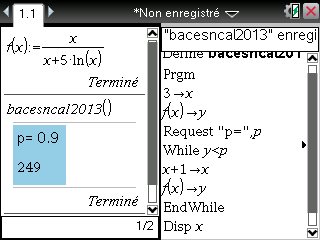
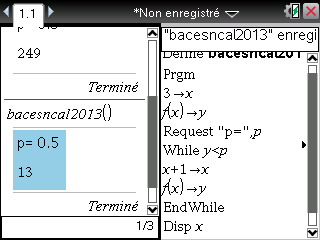
Là encore, le résultat de l'énoncé est confirmé et on obtient encore 13 jours pour p=0,5.
Enfin, voici pour les possesseurs de Casio Graph et Casio Prizm fx-CG toujours selon la même méthode:




Là encore, l'énoncé est confirmé et le résultat est 13 jours.
Bref, que vous soyez en série S, ES ou technologique, travaillez bien les algorithmes c'est la mode du moment!
Lien:
Sujet Maths BAC ES Nouvelle Calédonie novembre 2012















