Correction algo Olympiades Académiques 2013 1S Aix-Marseille

[critor]

Après le BAC et le Concours Général, aux Olympiades Académiques 2013 de 1ère sont tombés de nombreux algorithmes.

Intéressons-nous aujourd'hui à l'algorithmique qui est tombé en exercice 3 pour les Premières S dans l'Académie d'Aix-Marseille:

Question 1)a):
Nous étudions donc l'équation (E) 81a+125b+149c=2013, où a, b et c sont des entiers naturels.

Nous avons donc b≥0 et c≥0.
On en déduit 125b≥0 et 149c≥0.
Par sommation des inégalités, 125b+149c≥0

Mais l'équation (E) peut aussi s'écrire 125b+149c=2013-81a.
On en déduit 2013-81a≥0,

D'où: 2013≥81a
2013/81≥a
a≤2013/81

Comme a est un entier positif et que 2013/81≈24,9 on en déduit que 0≤a≤24.

On montre de même que b≤2013/125 et c≤2013/149, ce qui donne 0≤b≤16 et 0≤c≤13.



Question 1)b):
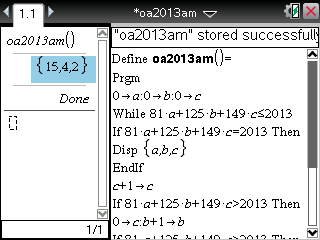
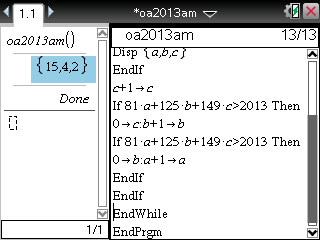
On nous demande donc maintenant d'écrire un algorithme recherchant tous les triplets (a,b,c) solutions de (E).

Il s'agit donc de vérifier l'équation (E) pour tous les triplets de valeurs possibles pour (a,b,c).

L'on peut faire cela en imbriquant 3 boucles 'pour':

Code: Select all

Pour a de 0 à 24 faire
   Pour b de 0 à 16 faire
      Pour c de 0 à 13 faire
         Si 81a+125b+149c=2013 alors
            Afficher (a,b,c)
         FinSi
      FinPour
   FinPour
FinPour


Remarquons que cet algorithme revient à tester 25*17*14=5950 triplets de valeurs.

Il est possible de traduire cet algorithme en un programme pour nos TI-Nspire, qui nous fournissent un seul triplet de solutions (15,4,2) en seulement quelques secondes!

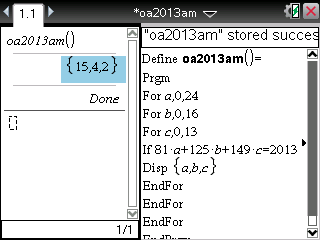
Le même programme est réalisable sur nos TI-82 à TI-84 ou Casio Graph/Prizm, mais il faudra cette fois-ci patienter quelques dizaines de secondes avant d'obtenir les mêmes solutions:

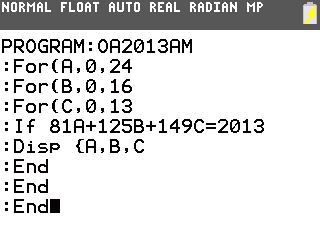
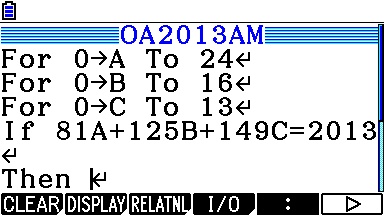
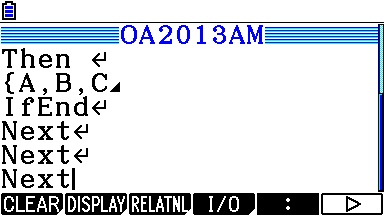
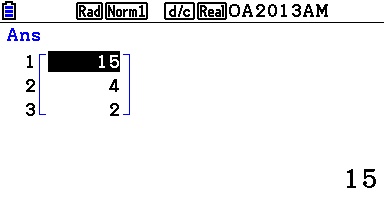
Sans doute est-ce à cause de ce long temps de calcul que la question suivante fait cadeau de a=15!



Jusqu'à présent les boucles 'pour' sont peu fréquentes au BAC, au profit de boucles 'tant que'.
C'est donc une excellente chose d'en parler aujourd'hui, afin de ne pas avoir de trou de mémoire le jour J si jamais...



Lien:
Olympiades Académiques de Mathématiques 2013 - 1èreS (Aix-Marseille)

[nikitouzz]

J'avais pas vu que Critor avait déjà corrigé l'algo mais du coup j'en ai fait un :

BASIC :

Code: Select all

:0→A→B→C
:tant que C=!14
: If 81A+125B+149C=2013
:  Disp "solution :","A=",A,"B=",B,"C=",C
: A+1→A
: If A=25
:  then
:  0→A
:  B+1→B
: End
: If B=17
:  then
:  0→B
:  C+1→C
: End
:End

Et en AXE pour montrer la puissance d'optimisations

Code: Select all

:0→A→B→C
:while1
: !If *149+81*A+125*B-2013
:  Disp "solution :","A=",A,"B=",B,"C=",C
: End
: A++-25??→A+1+B→B,B
: -17??→B+1+C→C,C
:End!If -14

[critor]

On sort du cadre de ce qui était attendu par l'énoncé je pense, mais voici une petite astuce d'optimisation.

Par exemple, lorsque a=10 et b=5 il est inutile d'incrémenter c au delà de 3 jusqu'à 13, car on dépasse alors strictement 2013 pour 81a+125b+149c.

Voici donc un nouvel algorithme avec une simple boucle 'tant que', qui teste et arrête d'incrémenter a, b et c lorsque l'on ne peut plus espérer trouver de solution pour des valeurs plus grandes.
(en conséquence, les valeurs 24, 16 et 13 de l'énoncé sont inutiles)



Au lieu de 5950 passages dans la boucle, je n'en ai plus que 1158!

[Bisam]

Ah bah non, c'était mon idée...
Mince, je n'ai pas été assez rapide !

[critor]

Ah, pas vu désolé.


On peut sûrement faire d'autres optimisations encore.

Si l'on parcourt les solutions dans un certain ordre, je pense que l'on n'est pas obligé de réinitialiser les compteurs b et c jusqu'à 0 lorsqu'ils 'dépassent'.

[Bisam]

Tant pis, je redonne une autre méthode (c'est la même, mais déguisée et en sautant une des boucles) :

Code: Select all

For a,0,24
  IntDiv(2013-81a,125)->d
  For b,0,d
    IntDiv(2013-81a-125b,149)->c
    If 81a+125b+149c=2013
       Disp {a,b,c}
  EndFor
EndFor

Avec ce code, on ne fait que 221 passages dans les boucles...

[Adriweb]

Joli


nikitouzz :

!If *149+81*A+125*B-2013
c'est pas un octet plus long que :
If *149+81*A+125*B=2013
?

[nikitouzz]

Non adriweb car l'axe est un langage compilé faut donc connaitre le compilateur cependant je viens d'avoir une superidée pour otpimiser je poste le code des qu ej le paufine par contre impossible de le faire en basic je le poste donc en axe.

EDIT :

Code: Select all

:0→A→B→C
:while1
: !If C*149+(81*(A^24))+((B^16)*125)-2013
:  Disp "solution :","A=",A^24>dec,"B=",B^16>dec,"C=",C
: End
: (A++^24=0)+B->B
:(^17=0)+C->C
:End!If -14

voila