Il s'agit donc d'étudier les déplacements d'une cible chaque seconde entre trois positions 1, 2, 3 selon les règles suivantes:
- la cible commence en 1
- de 1 et de 3, la cible va en 2
- de 2, la cible va en 1 ou 3 de façon équiprobable
L'on peut représenter cette situation à l'aide d'un graphe probabiliste:
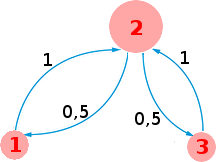
Selon le graphe en partant de 1, après un nombre impair de secondes/déplacements, on est forcément en 2.
Après un nombre pair non nul de déplacements, on se retrouve de façon équiprobable, soit en 1, soit en 3.
Question A)1) 1/2
Question A)2)a) 0
Question A)2)b) 1
Question A)3)a) 1/2
Question A)3)b) 0
Question A)4) 0

Notons que cet algorithme est fort mal écrit - avec une fonction EntAlea() qui n'est ni du langage naturel ni du langage mathématique, des parenthèses pour des affichages et des points virgule de séparation de paramètres ou de ponctuation d'instructions.
Un excellent exemple de ce qu'il ne faut pas faire au BAC!

Cela ressemble fortement à un langage de programmation car il y a des contraintes de syntaxe et l'auteur en aurait donc rapidement traduit les instructions en français, ce qui justement n'est pas un algorithme.
Les trous à compléter dans l'algorithme correspondent simplement aux cas étudiés ci-dessus.
On peut donc les compléter de la façon suivante:
- Code: Select all
Variables: n entier
Début
Entrer n
Si n est impair alors
Afficher "Cible à position 2"
sinon
Si EntAlea(0,1)=0 alors
Afficher "Cible à position 1"
sinon
Afficher "Cible à position 3"
FinSi
FinSi
Fin
L'on vérifie aisément le fonctionnement correct de l'algorithme en le traduisant en un programme pour notre calculatrice.
Le test de parité de N peut utiliser la fonction partie entière afin de vérifier si N est divisible par 2 ou non.
Voici un programme pour TI-82 à TI-84:


En voici maintenant un pour Casio Graph/Prizm:



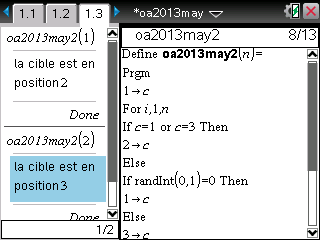
Et enfin maintenant, voici une version TI-Nspire:
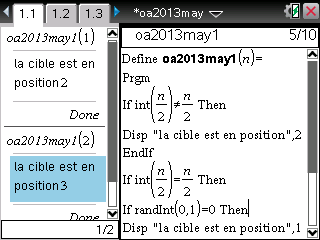
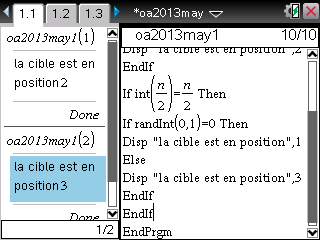

Encore un 'algorithme' assez mal écrit pour les mêmes raisons que le précédent, d'autant plus qu'il y a deux instructions 'Si' mais un seul 'FinSi'.
Cette fois-ci on utilise une boucle "pour i=... à n faire".
n étant le nombre de déplacements de la cible, nous allons mettre "pour i=1 à n faire" afin de passer exactement n fois dans la boucle.
La cible va en 2 lorsque qu'elle est en 1 ou 3.
Nous complétons donc l'instruction conditionnelle avec "Si C=2 ou C=3".
Enfin, nous avons des affectations de C avec 2 et 1, la dernière affectation correspond donc forcément par élimination à 3, et nous mettons "Sinon C←3".
Voici l'algorithme:
- Code: Select all
Variables: n, C, i entiers
Début
Entrer n
C←1
Pour i=1 à n faire
Si C=1 ou C=3 alors
C←2
sinon
Si EntAlea(0,1)=0 alors
C←1
sinon
C←3
FinSi
FinSi
FinPour
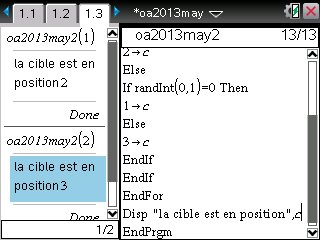
Afficher "la cible est en position", C
Fin
L'on vérifie encore une fois que l'algorithme est bon en testant sur calculatrice.
Voici un programme traduisant cet algorithme pour TI-82 à TI-84:
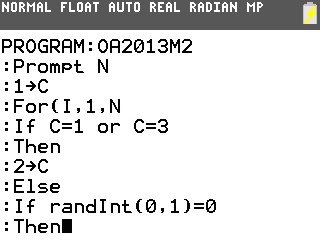

Voici maintenant une version pour Casio Graph/Prizm:



Et voici enfin une version TI-Nspire:
Au final, quelles sont les différences entre ces deux algorithmes?
L'algorithme n°1 n'utilise aucune boucle. Il utilise simplement les règles de probabilité établies dans les questions précédentes.
Il s'exécute donc en un temps constant sur machine, quelle que soit la valeur de n. On dit que sa complexité est en o(1).
L'algorithme n°2 par contre a une toute autre approche et simule réellement à l'aide d'une boucle 'pour' la totalité des n déplacements de la cible.
C'est donc un algorithme linéaire de complexité en o(n), dont le temps d'exécution sur machine sera proportionnel à n.
En complexité, l'algorithme 1 serait donc meilleur et la simulation complète effectuée de l'algorithme n°2 serait inutile dans le contexte de ce qu'il doit renvoyer dans cet exercice.
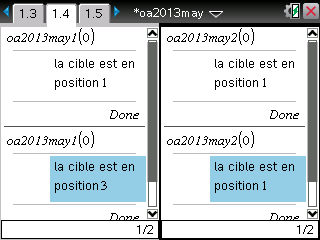
Notons toutefois un petit bémol, avec le cas particulier n=0 interdit par l'énoncé.
Après 0 déplacement, la cible est par définition en position 1, la position d'origine.
L'algorithme n°2 qui simule tous les détails des déplacements est parfaitement d'accord avec ça.
Mais l'algorithme n°1 se plante une fois sur deux, en nous expliquant que la cible est en position 3 au temps 0, ce qui est impossible!

Lien:
Olympiades Académiques de Mathématiques 2013 - 1ère (Mayotte)
















