SuperSpire (S²) : extension calculs pour TI-Nspire CAS et non-CAS
Actions
Vote (3.67/5):
ScreenshotAperçu
Informations
Catégorie :Category: Maths TI-Nspire
Auteur Author: Xavier Andréani
Type : Classeur
Taille Size: 57.64 Ko KB
Mis en ligne Uploaded: 02/02/2014 - 16:12:50
Mis à jour Updated: 12/02/2014 - 01:43:44
Uploadeur Uploader: critor (Profil)
Téléchargements Downloads: 2691
Visibilité Visibility: Archive publique
Shortlink : http://ti-pla.net/a29172
Type : Classeur
Taille Size: 57.64 Ko KB
Mis en ligne Uploaded: 02/02/2014 - 16:12:50
Mis à jour Updated: 12/02/2014 - 01:43:44
Uploadeur Uploader: critor (Profil)
Téléchargements Downloads: 2691
Visibilité Visibility: Archive publique
Shortlink : http://ti-pla.net/a29172
Description
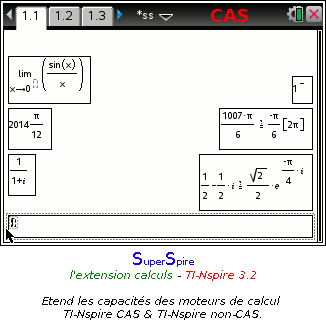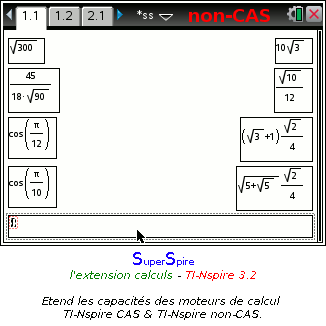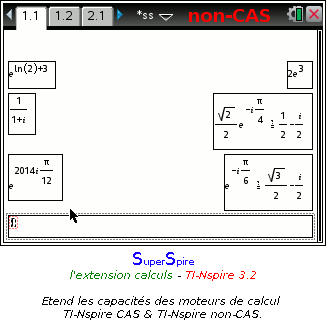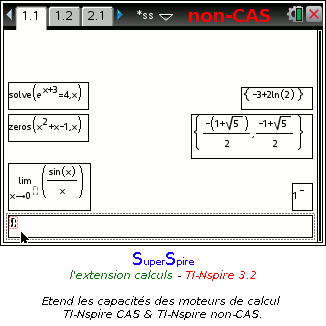
Application de calculs étendant les capacités des moteurs de calcul TI-Nspire CAS et non-CAS.
Interface Lua, OS 3.2 ou plus requis
Sur TI-Nspire CAS:
- précise si les limites sont atteintes valeurs supérieures ou inférieures
- précise la mesure principale des résultats en radians
- précise les formes algébriques et exponentielles des nombres complexes
Sur TI-Nspire non-CAS:
- résultats exacts grâce à un moteur de calcul exact gérant de nombreuses formes (fractions, radicaux, radians et trigonométrie, exponentielles, logarithmes...)
- résolution d'équations à un ou plusieurs solutions numériques
- calcul de limites
- précise si les limites sont atteintes valeurs supérieures ou inférieures
- précise la mesure principale des résultats en radians
- précise les formes algébriques et exponentielles des nombres complexes
Interface personnalisable :

Interface Lua, OS 3.2 ou plus requis
Sur TI-Nspire CAS:
- précise si les limites sont atteintes valeurs supérieures ou inférieures
- précise la mesure principale des résultats en radians
- précise les formes algébriques et exponentielles des nombres complexes
Sur TI-Nspire non-CAS:
- résultats exacts grâce à un moteur de calcul exact gérant de nombreuses formes (fractions, radicaux, radians et trigonométrie, exponentielles, logarithmes...)
- résolution d'équations à un ou plusieurs solutions numériques
- calcul de limites
- précise si les limites sont atteintes valeurs supérieures ou inférieures
- précise la mesure principale des résultats en radians
- précise les formes algébriques et exponentielles des nombres complexes
Interface personnalisable :

Archive contentsContenu de l'archive
News articles referring to this archiveNews mentionnant cette archive
Les complexes? Pas si complexe que ça... (14626) (19/03/2014) [News TI-Nspire]
















