Dans une
news précédente, nous te confirmions avec le sujet de Polynésie française, pour la 3ème fois en 4 sujets de maths inédits du BAC S 2012, que tu pouvais être interrogé dans ton épreuve sur les ajouts du nouveau programme de maths commencé en Seconde en 2009, et notamment l'algorithmique.
Comme nous l'avions déjà fait les 2
fois précédentes, nous te donnions alors quelques
éléments de corrections sur l'algorithme qu'il fallait analyser en partie A de l'exercice 3.
Le nouveau programme de maths détaillait trois compétences évaluables pour l'algorithmique:
- Savoir dérouler et interpréter un algorithme écrit en langage naturel
- Savoir produire un algorithme en langage naturel pour répondre à un problème
- Savoir implémenter un algorithme sur sa calculatrice programmable ou sur un logiciel de mathématiques
La partie A concernait donc la 1ère compétence.
Mais si nous allons un peu plus loin, la dernière question de la partie B du même exercice demande de produire un algorithme!
Cela fait donc deux questions d'algorithmique dans le même sujet!
Voyons donc un peu ça aujourd'hui:
Il s'agit donc de produire un algorithme de recherche du rang à partir duquel la suite dépasse une certaine valeur, ici u
n≥1000.
C'est donc exactement le même type d'algorithme que celui demandé dans le
sujet d'Amérique du Nord.
Nous allons donc produire un algorithme similaire de recherche par balayage en incrémentant le rang k à partir de 0.
Pour cela, nous utiliserons une boucle
"tant que" avec comme condition de poursuite le contraire logique de la condition recherchée, ici: u
k<1000.
Pour le calcul de la valeur de u
n dans la condition, utilisons tout simplement la formule générale de la suite donnée à la question B)4)b): u
n=3
n+n-1.
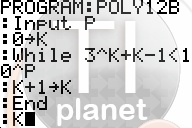
Afin de vérifier si notre algorithme semble correct, on peut le traduire en un programme sur calculatrice TI-73 à TI-84:
Contrairement au
programme d'Amérique du Nord, nous obtenons cette fois-ci un résultat en un temps raisonnable!
Le résultat 7 confirme d'ailleurs celui trouvé à la question précédente dans la
news précédente!
Notons qu'il était également possible d'utiliser la définition par récurrence de la suite u
n pour calculer la condition. Cela nécessite d'utiliser 2 variables: une pour stocker le rang de la suite
(k) et une 2ème pour stocker la valeur précédente de la suite nécessaire au calcul par récurrence.
Cette récurrence est donc un petit peu plus compliqué du point de vue algorithmique, mais très similaire à ce que fait l'algorithme de la partie A qui n'est donc pas là pour rien.
Là encore, après modification du programme, la calculatrice confirme le résultat précédent:
Liens:Sujets inédits du BAC S 2012 toutes matières + corrigés 
Sujets inédits du BAC S 2012 anticipé toutes matièresKit de réussite TPs SVT du BAC S 2012: sujets + corrigésSujets inédits du BAC ES 2012 toutes matières + corrigés Sujets inédits du BAC ES 2012 anticipé toutes matièresSujets inédits du BAC L 2012 anticipé toutes matièresSujets inédits du BAC STG 2012 toutes matières + corrigés Sujets inédits du BAC STG 2012 anticipéSujets inédits du BAC ST2S 2012 toutes matières Sujets inédits du BAC ST2S 2012 anticipéSujets inédits du BAC STL 2012 + corrigés Sujets inédits du BAC STL 2012 anticipéSujets inédits du BAC STI 2012 toutes matières + corrigés Sujets inédits du BAC STI 2012 anticipé toutes matières
by 
:
pour entrer la suite récurrente définie par u0=0 et un+1=3un-2n+3.
:
