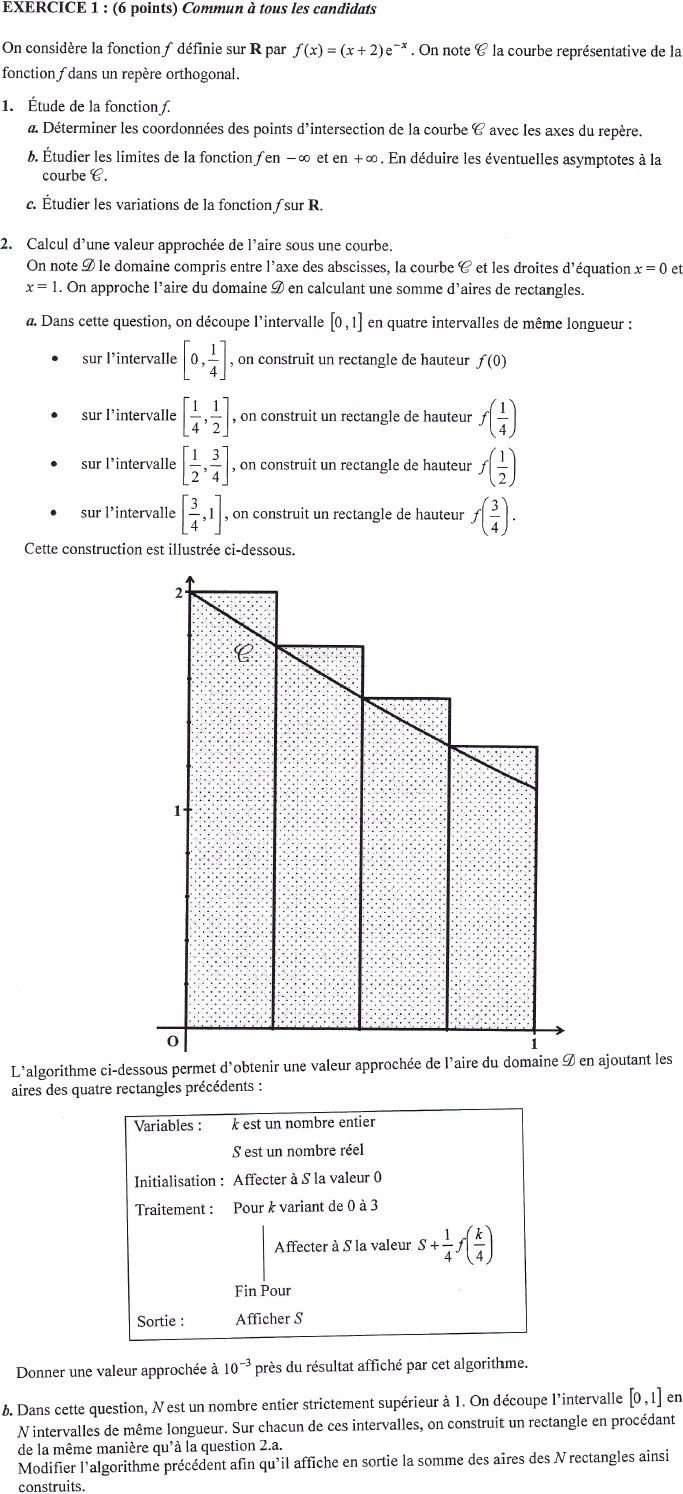
Il y a toutefois une petite originalité, puisque pour une fois l'algorithme ne tombe pas dans le contexte d'un exercice de suites mais de fonctions.
Question 2)a)
On nous propose donc un algorithme calculant une valeur approchée d'une intégrale par la méthode des rectangles.
On nous demande donc ce qu'il affiche, et il nous suffit de le programmer sur notre calculatrice graphique pour avoir la réponse.
Toutefois ici, l'algorithme utilise une fonction f dans une affectation.
On peut faire l'affectation en question telle quelle sur une calculatrice utilisant un langage de programmation fonctionnel comme la TI-Nspire.
Les autres calculatrices comme les TI-82 à TI-84 et Casio Graph/Prizm utilisent un langage de programmation procédural, ce qui va nécessiter quelques petites adaptations.
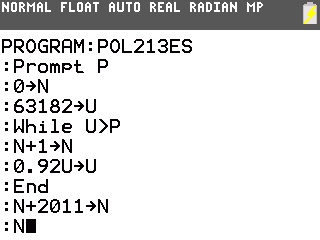
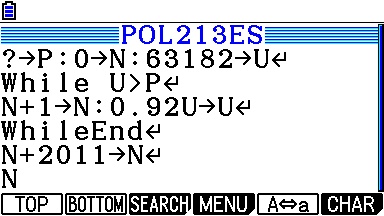
Voici donc des traductions possibles de l'algorithme pour toute calculatrice TI-76/82/83/84 et Casio Graph/Prizm:
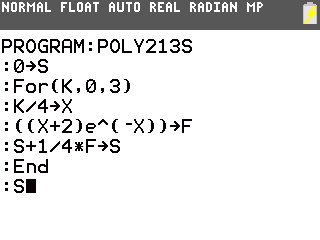

Et voici maintenant ce qu'ils affichent:


La réponse est donc 1,642 à 10-3 près.
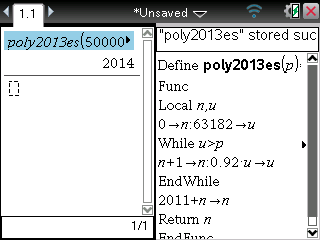
La même chose est donc réalisable beaucoup plus aisément sur TI-Nspire/89/92/Voyage200:
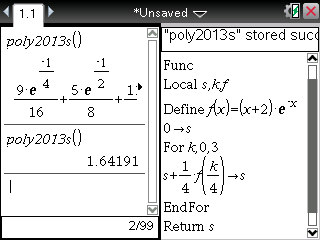
Si nous sommes sur une TI-Nspire CAS ou une TI-89/92/Voyage200, par défaut la calculatrice utilise son moteur de calcul formel et donne un résultat exact.
Mais il suffit par exemple sur TI-Nspire CAS de lancer le programme en forçant l'utilisation du moteur de calcul numérique approché, en validant avec
![[ctrl] :nsct:](./images/smilies/nspire/ns_ct.png)
![[enter] :nsen:](./images/smilies/nspire/ns_en.png)
Question 2)b)
L'algorithme précédent utilise donc 4 rectangles pour déterminer son approximation.
On aimerait ici une modification utilisant un nombre N de rectangles.
Il va donc suffire de saisir le nombre de rectangles voulus (instruction d'entrée) en début d'algorithme.
Puisque pour N=4 les bornes de la boucle 'pour' étaient 0 et 3, pour N rectangles les bornes sont donc 0 et N-1.
Voici l'algorithme modifié en conséquence:
- Code: Select all
Variables:
k est un nombre entier
S est un nombre réel
Entrées:
Saisir N
Initialisation:
Affecter à S la valeur 0
Traitement:
Pour k variant de 0 à N-1
Affecter à S la valeur S+1/N*f(k/N)
FinPour
Sortie:
Afficher S
On peut vérifier astucieusement la justesse de cet algorithme en modifiant en conséquence notre programme sur calculatrice, et en vérifiant qu'il continue de retourner la même valeur pour N=4:
Voici la modification pour TI-76/82/83/84 et pour Casio Graph Prizm:


Effectivement, c'est toujours le même résultat!



Et voici maintenant la modification pour TI-Nspire, qui confirme encore une fois le résultat:
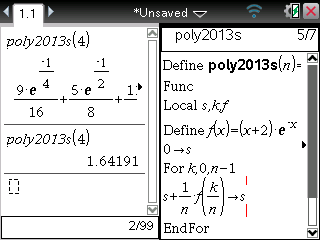
A bientôt 

Liens:
BAC S 2013: Maths Obligatoire (Polynésie - juin 2013)
BAC S 2013: Maths Spécialité (Polynésie - juin 2013)
BAC S 2013: Annales des sujets inédits corrigés toutes matières