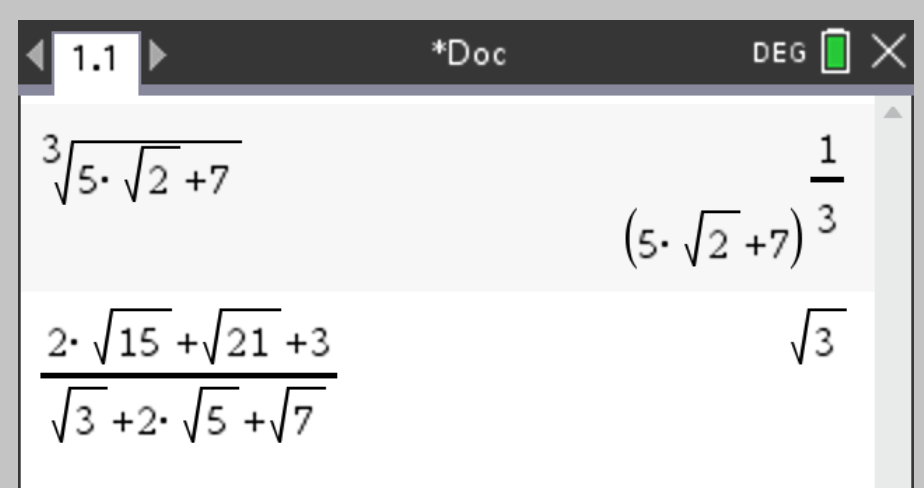by parisse » 15 Apr 2023, 19:52
by parisse » 15 Apr 2023, 19:52
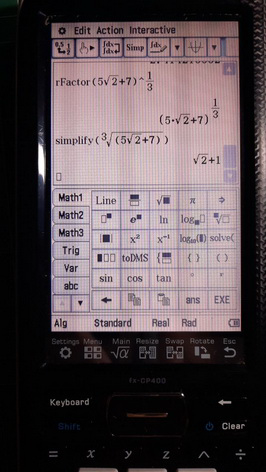
This is not the right way to simplify roots. The right way here is to factor x^3-(5*sqrt(2)+7) over Q[sqrt(2)], and to do that multiply by the conjugate, this gives x^6-14*x^3-1, factor it over the integers, you get 2 factors (x^2-2*x-1)*(x^4+2*x^3+5*x^2-2*x+1), then select the right one. If the polynomial is irreducible over the integers, then it can not be simplified (in that case the algebraic extension is of order 6).
Note that the general tool for something more complicated than sqrt is the resultant.
r:=resultant(x^3-(5y+7),y^2-2,y);
factor(r);
(you can run these commands with KhiCAS on compatible calculators, and on the Prime)