by Le voici:
Question 4)a):
On nous demande donc une sorte de trace de l'algorithme, avec les états des variables lors des différentes itérations de la boucle.
Selon une astuce rappelée hier soir, il suffit de prendre notre calculatrice TI-76/82/83/84, d'y programmer l'algorithme en question, et de rajouter une instruction de sortie dans la boucle.
L'énoncé donnant le début de la trace, on peut déterminer l'endroit exact où placer cet affichage.
Il doit donc se faire avant les modifications de A et B (A et B valant toujours leurs valeurs d'initialisation 0 et 1 à la 1ère étape), mais après l'affectation de M qui n'aurait pas de valeur sinon.
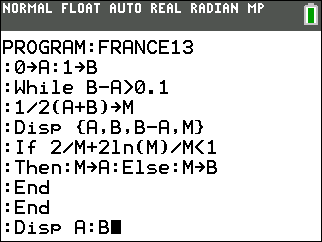
On obtient alors directement sur l'écran de la calculatrice les résultats à recopier:
L'étape 5 ne correspond pas à un passage dans la boucle, donc son détail semble discutable. M n'est en effet pas modifié.
Mais ceux qui n'ont pas fait sur machine et ont déroulé l'algorithme de dichotomie à la main auront peut-être mis une valeur différente.
Pour ma part, je réponds exactement à la question de l'énoncé en ne modifiant pas la valeur de M entre les étapes 4 et 5, c'est-à-dire en donnant sa vraie valeur.
| étape 1 | étape 2 | étape 3 | étape 4 | étape 5 | |
| a | 0 | 0 | 0,25 | 0,375 | 0,4375 |
| b | 1 | 0,5 | 0,5 | 0,5 | 0,5 |
| b-a | 1 | 0,5 | 0,25 | 0,125 | 0,0625 |
| m | 0,5 | 0,25 | 0,375 | 0,4375 | 0,4375 |
Il est à mon avis fort possible que les deux possibilités soient acceptés dans les consignes de correction pour la 5ème étape.
La même chose reste bien entendue réalisable si vous aviez une Casio Graph/Prizm...
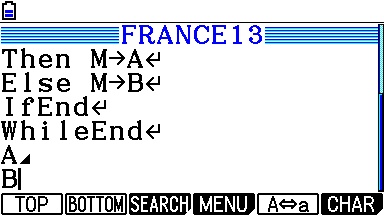
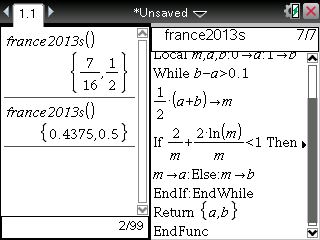
... ou encore sur TI-Nspire, et il ne faut pas oublier d'évaluer en mode approché sur TI-Nspire CAS avec
Question 4)b):
Cet algorithme recherche par dichotomie sur l'intervalle [a,b]=[0,1], un encadrement d'amplitude au plus 0,1=10-1 (condition de poursuite de la boucle tant que) de α tel que f(α)=1.
C'est cet encadrement [a,b] qui est affiché à la fin et vaut ici [0,4375;0,5].
Question 4)c):
La 2ème solution β de l'équation f(x)=1, ne se trouve pas sur l'intervalle [0,1], mais sur [1,+∞[.
Pour la rechercher, il suffit donc de modifier l'intervalle [a,b] de départ, de [0,1] à par exemple [1,6], et de tenir compte du fait que f est décroissante sur cet intervalle.
Voici l'algorithme avec les modifications indiquées:
- Code: Select all
Variables:
a,b et m sont des réels
Initiatlisation:
Affecter à a la valeur 1 (*)
Affecter à b la valeur 6 (*)
Traitement:
Tant que b-a>0,1
Affecter à m la valeur 1/2(a+b)
Si f(m)>1 alors affecter à a la valeur m (*)
sinon affecter à b la valeur m
Fin de Si
Fin de Tant que
Sortie:
Afficher a
Afficher b
On confirme le bon fonctionnement sur calculatrice TI-76/82/83/84:
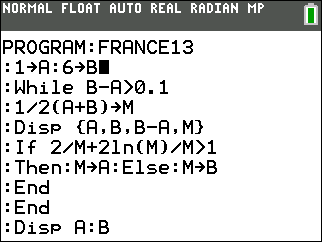
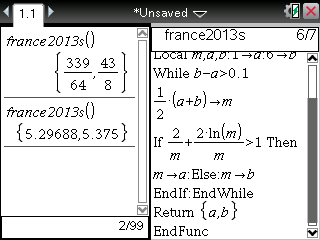
Un encadrement à 10-1 près de β est donc [5,296875;5,375].
Voici la même modification pour Casio Graph/Prizm...
... et maintenant pour TI-Nspire:
Lien:
BAC S 2013 - Annales des sujets toutes matières et corrections
