Sur les modèles milieu de gamme de Casio (Graph 35+E II, Graph 90+E, Graph Math+) et Texas Instruments (TI-82 Advanced Edition Python, TI-83 Premium CE Edition Python), le moteur en question est de type QPiRac. C'est-à-dire qu'il se base sur des propriétés remarquables (notamment sur les parties décimales) pour identifier et afficher correctement les nombres appartenant aux 2 familles suivantes :
- famille QPi (multiples rationnels de π) : $mathjax$\pm\frac{a\pi}{b}$mathjax$(pour les angles remarquables en radians notamment)
- famille QRac (binômes de rationnels et/ou radicaux) : $mathjax$\frac{\pm a\sqrt{b} \pm c\sqrt{d}}{f}$mathjax$(ce qui couvre un large ensemble allant des fractions du collège aux racines de polynômes du 2nd degré en Première, en passant par nombre de valeurs remarquables en trigonométrie)
Casio | TI | NumWorks |
Il est à noter que ce n'est hélas plus le cas de nos jours. Depuis l'année scolaire 2019-2020, les exponentielles sont abordées en spécialité Mathématiques dès la classe de Première Générale.
Là où la concurrence se contente d'écritures décimales approchées dès que l'on sort des deux familles précédentes, la NumWorks à la différence a l'immense avantage d'être capable de retourner une valeur exacte pour n'importe quelle saisie algébrique ! 👍
Casio | TI | NumWorks |

 À l'origine la NumWorks était même encore plus géniale que cela. Le moteur faisant appel non pas à des algorithmes numériques mais à des algorithmes de traitement d'arbres, les noeuds pouvaient être aussi bien des valeurs numériques que des lettres ou expressions littérales. Il était ainsi possible de saisir des expressions littérales et d'en obtenir une simplification en résultat (développement + réduction) ! 👍
À l'origine la NumWorks était même encore plus géniale que cela. Le moteur faisant appel non pas à des algorithmes numériques mais à des algorithmes de traitement d'arbres, les noeuds pouvaient être aussi bien des valeurs numériques que des lettres ou expressions littérales. Il était ainsi possible de saisir des expressions littérales et d'en obtenir une simplification en résultat (développement + réduction) ! 👍Cette fonctionnalité rajoutée dès décembre 2017 avec la mise à jour 1.2 du firmware officiel Epsilon fut malheureusement désactivée en juin 2019 avec la mise à jour 11.2, NumWorks estimant qu'elle constituait un obstacle à ses projets d'expansion à l'international, nombre de nos voisins européens interdisant en effet déjà toute fonctionnalité de calcul littéral ou formel à leurs examens de l'enseignement secondaire.
 Toutefois le fonctionnement interne de Poincaré n'a pas changé. Les arbres continuent à pouvoir mélanger noeuds numériques et littéraux, et le moteur continue à procéder aux simplifications par développements et réductions. C'est juste à la fin si l'expression correspondant à l'arbre obtenu après traitement fait encore appel à des termes littéraux, que le résultat affiché est au dernier moment remplacé par la valeur undef.
Toutefois le fonctionnement interne de Poincaré n'a pas changé. Les arbres continuent à pouvoir mélanger noeuds numériques et littéraux, et le moteur continue à procéder aux simplifications par développements et réductions. C'est juste à la fin si l'expression correspondant à l'arbre obtenu après traitement fait encore appel à des termes littéraux, que le résultat affiché est au dernier moment remplacé par la valeur undef.Pour ceux qui disposent d'une calculatrice NumWorks N0100 (arrêtée pour la rentrée 2019) ou N0110 (arrêtée pour la rentrée 2023), il est ainsi possible de réactiver le calcul littéral en installant un firmware Omega ou Upsilon. Ces firmwares tiers sont des forks améliorés du firmware officiel Epsilon, et entre autres retirant justement la limitation précédente.
 Et précisons de plus qu'avec la mise à jour Epsilon 15.3 de janvier 2021, NumWorks avait changé son algorithme de détermination de nombres dérivés. L'algorithme numérique pouvant retourner des résultats faux dans bien des cas particuliers avait été remplacé par une véritable dérivation de l'expression de la fonction au niveau de l'arbre de calcul, autrement plus fiable.
Et précisons de plus qu'avec la mise à jour Epsilon 15.3 de janvier 2021, NumWorks avait changé son algorithme de détermination de nombres dérivés. L'algorithme numérique pouvant retourner des résultats faux dans bien des cas particuliers avait été remplacé par une véritable dérivation de l'expression de la fonction au niveau de l'arbre de calcul, autrement plus fiable.Les firmwares tiers Omega et Upsilon exploitent fort avantageusement ce nouvel algorithme, en te permettant d'obtenir l'expression littérale de la fonction dérivée ! 👍
Pour cela, dans ta saisie demandant le nombre dérivé en une valeur, il suffit de remplacer la valeur en question par la variable de la fonction.
Mais concernant les développement et réduction d'expressions littérales il y a toutefois une astuce si tu sais faire preuve d'un minimum de malice.
 Si ton expression ne fait intervenir au maximum que 3 paramètres, il te suffit de remplacer chaque paramètre de l'expression par une des 3 constantes numériques suivantes qui à la différence sont parfaitement autorisées à intervenir dans les arbres-résultats : π, e et i. La seule chose à laquelle il faut faire attention lors de ce choix, c'est à ce qu'aucune des propriétés spécifiques à la constante en question n'intervienne lors de la simplification de l'expression.
Si ton expression ne fait intervenir au maximum que 3 paramètres, il te suffit de remplacer chaque paramètre de l'expression par une des 3 constantes numériques suivantes qui à la différence sont parfaitement autorisées à intervenir dans les arbres-résultats : π, e et i. La seule chose à laquelle il faut faire attention lors de ce choix, c'est à ce qu'aucune des propriétés spécifiques à la constante en question n'intervienne lors de la simplification de l'expression.Exemple : pour développer et réduire
Nous évoquerons par la suite l'utilisation de cette astuce en tant que pseudo-calcul littéral.

 Et bien NumWorks vient tout juste de lancer le bêta-test public de sa prochaine mise à jour Epsilon 24. Et sans pour autant invalider les deux pistes précédentes, cette mise à jour révèle un autre grand projet.
Et bien NumWorks vient tout juste de lancer le bêta-test public de sa prochaine mise à jour Epsilon 24. Et sans pour autant invalider les deux pistes précédentes, cette mise à jour révèle un autre grand projet.2 versions du firmware ont été diffusés à ce jour :
- 24.0.0 le 11 décembre 2024
- 24.0.1 dès le 12 décembre 2024
Pour cela calculons en mode degrés
Le résultat théorique est de 9. Toutefois les calculatrices numériques ne travaillant pas sur la totalité de l'ensemble des nombres réels, ni même sur celui des nombres décimaux, mais sur un tout petit sous-ensemble de nombres dits en virgule flottante, répondent presque toutes une valeur approchante, que nous appelons signature trigonométrique.
Du temps où les calculatrices disposaient de fort peu de mémoire et déléguaient intégralement au matériel les divers algorithmes de calcul, cette signature permettait d'identifer la famille de processeur utilisée.
De nos jours c'est encore partiellement vrai sur les calculatrices scientifiques, mais plus du tout sur les calculatrices graphiques où les algorithmes de calcul relèvent intégralement ou presque du logiciel.
Toutefois le test reste pertinent, la signature permettant malgré tout d'identifier le moteur de calcul utilisé, et ce peu importe qu'il soit logiciel ou matériel.
Avec son traitement non pas numérique mais via des arbres de l'expression saisie, la NumWorks se démarquait jusqu'ici avec un résultat correct de 9. Précisons que c'est extrêmement rare. On peut citer dans ce cas les Kinpo SG1 et SG2, des calculatrices graphiques qui ont été commercialisées exclusivement en marque blanche (Citizen SRP-325G et HP 9g pour la SG1, Citizen SRP-400G et Datexx DS-883 pour la SG2).
Et bien avec Epsilon 24 il y a du changement, le résultat passe de façon totalement inattendue de 9 à 8.9999999995623 :
Epsilon ≤23 | Epsilon 24 |
Cela nous indique que le moteur de calcul a été complètement remplacé (nous ignorons d'ailleurs si il conserve le nom de Poincaré suite à ce changement majeur).
La signature trigonométrique 8.9999999995623 étant de plus jusqu'à aujourd'hui totalement inconnue de l'Internet, cela indiquerait également un moteur de calcul venant d'être développé spécifiquement pour la NumWorks (et non l'utilisation ou achat d'un moteur de calcul déjà développé par une entité tierce).
Dur à confirmer sans accès au code source, mais la nouvelle signature nous suggère de plus que le nouveau moteur n'utiliserait plus les arbres de calculs.
On peut donc s'attendre à bien des changements en conséquence, mais a priori, vu les caractéristiques précédentes géniales et à ce jour exclusives qui faisait toute la supériorité de la calculatrice NumWorks dans le milieu de gamme, nous ne sommes pas très rassurés d'un point de vue utilisateurs...
Epsilon ≤23 | Epsilon 24 |
Si le nouveau moteur de calcul ne procède plus en priorité par développements-réductions (peu importe que ce soit sur des objets de type arbre ou autre), cela peut se comprendre. Nous ignorons toutefois à ce jour le caractère définitif ou pas de cette lourde régression.
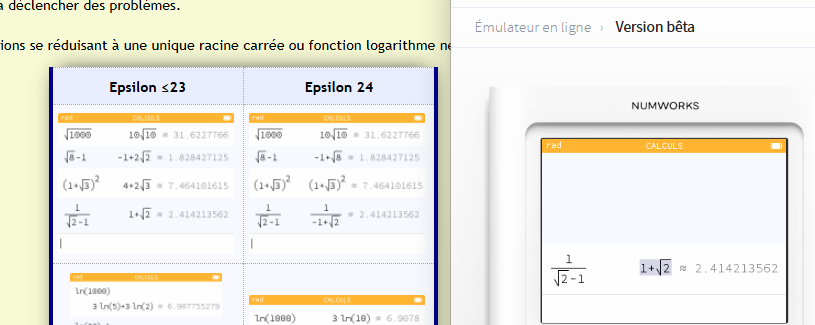
Déjà pour ne pas chercher compliqué, des expressions se réduisant à une unique racine carrée ou fonction logarithme ne sont souvent plus simplifiées correctement :
Epsilon ≤23 | Epsilon 24 |
La simplification a parfois lieu (de façon possiblement différente et non optimale), mais bien souvent plus du tout (l'expression saisie étant retournée à l'identique).
Si la calculatrice est configurée en notation Algébrique pour les complexes, les expressions saisies peuvent ne pas être simplifiées, et lorsqu'elles le sont ne même pas respecter la notation en question :
Epsilon ≤23 | Epsilon 24 |
Si la calculatrice est configurée en notation Exponentielle pour les complexes, à la différence il y a bien respect de la notation en question, mais ce n'est pas forcément davantage utile dans le sens où la calculatrice est capable de te réponse que la notation exponentielle de ta saisie c'est littéralement (sans simplification)
Epsilon ≤23 | Epsilon 24 |
Epsilon ≤23 | Epsilon 24 |
Avec des arbres de calcul, elles devaient nécessiter pas mal de ressources mémoire. Et effectivement, si les arbres de calcul ont été remplacés, cela expliquerait des sommes plus ambitieuses de termes permettant notamment une meilleure exploration des séries numériques.
Toutefois dans le cadre des graphes tracés avec l'application Grapheur, nous avons quelques surprises...
Epsilon ≤23 | Epsilon 24 | |
 Pourquoi ? Voici une piste, rappelons que les nombres complexes ne sont pas loin dans ce cas. Par exemple :
Pourquoi ? Voici une piste, rappelons que les nombres complexes ne sont pas loin dans ce cas. Par exemple :- avec la notation complexe réglée sur Réel : $mathjax$\sqrt[3]{-8}=-2$mathjax$
- avec la notation complexe réglée sur Algébrique : $mathjax$\sqrt[3]{-8}=1+i\sqrt{3}$mathjax$
Autre hypothèse, peut-être que lors des calculs internes pour x<0 le moteur passe ici à un moment ou un autre sur l'ensemble des nombres complexes, mais oublie à la fin de repasser sur l'ensemble des nombres réels pour les résultats réels. Ceci expliquerait l'absence d'images affichées pour tout x<0.
Une racine peut également s'écrire en tant que puissance. Par exemple,
Epsilon ≤23 | Epsilon 24 | |
 Très étrange car ici encore, l'image f(-6,4) existe parfaitement si on l'appelle depuis l'onglet Tableau ou encore l'application Calculs… Peut-être donc bien comme évoqué l'opération de mise à la puissance qui dans certaines conditions spécifiques passerait par l'ensemble des nombres complexes pour retourner un résultat réel, mais qui ne serait pas détecté comme tel par le grapheur.
Très étrange car ici encore, l'image f(-6,4) existe parfaitement si on l'appelle depuis l'onglet Tableau ou encore l'application Calculs… Peut-être donc bien comme évoqué l'opération de mise à la puissance qui dans certaines conditions spécifiques passerait par l'ensemble des nombres complexes pour retourner un résultat réel, mais qui ne serait pas détecté comme tel par le grapheur.Epsilon ≤23 | Epsilon 24 |
Pour tenter d'y voir un peu mieux, passons à une fonction f non constante pour x<0, par exemple d'expression
Epsilon ≤23 | Epsilon 24 | |
 On note ici aussi anormalement sur Epsilon 24 un tracé étrangement moins lisse, et au moins 2 valeurs interdites retournant comme image undef : -6,4 et -0,2. Et pourtant ici encore aucun problème avec les images si appelées autrement que via le graphe.
On note ici aussi anormalement sur Epsilon 24 un tracé étrangement moins lisse, et au moins 2 valeurs interdites retournant comme image undef : -6,4 et -0,2. Et pourtant ici encore aucun problème avec les images si appelées autrement que via le graphe.Tiens pour voir, tentons de tracer le graphe symétrique par l'axe horizontal, en définissant la fonction g d'expression
Epsilon ≤23 | Epsilon 24 | |
 Très étrange, contrairement à ce à quoi nous aurions pu nous attendre, ici les valeurs interdites donnent pour image non pas undef mais +∞, avec des erreurs de tracé qui nous permettent de remarquer qu'il y a beaucoup plus que 2 cas problématiques...
Très étrange, contrairement à ce à quoi nous aurions pu nous attendre, ici les valeurs interdites donnent pour image non pas undef mais +∞, avec des erreurs de tracé qui nous permettent de remarquer qu'il y a beaucoup plus que 2 cas problématiques...Epsilon ≤23 | Epsilon 24 | |
 Puisque l'on change radicalement de moteur de calcul, il nous faut réévaluer les performances.
Puisque l'on change radicalement de moteur de calcul, il nous faut réévaluer les performances.Pour les calculatrices munies de l'opérateur de sommation, nous comparons habituellement les performances en chronométrant le temps de calcul de la somme suivante, en mode degrés :
Epsilon 23 | Epsilon 24 | |
NumWorks N0110/N0115 | 1.103s | 0.521s |
NumWorks N0120 | 0.252s | 0.0355s |
Les différentes calculatrices NumWorks progressent nettement sur ce test, mais pas dans les mêmes proportions :
- 2 fois moins de temps sur calculatrices NumWorks N0110/N0115
- mais 7 fois moins de temps sur calculatrice NumWorks N0120, à croire qu'il y a désormais des lignes spécifiques à son processeur dans le code source

 Autre test certes moins précis, mais avec l'avantage de permettre de comparer toutes les calculatrices graphiques entre elles, même les premières à partir de 1985 ou encore les clones bas de gamme, car elles sont toutes capables de tracer au moins 1 graphe de fonction.
Autre test certes moins précis, mais avec l'avantage de permettre de comparer toutes les calculatrices graphiques entre elles, même les premières à partir de 1985 ou encore les clones bas de gamme, car elles sont toutes capables de tracer au moins 1 graphe de fonction.Il s'agit de chronométrer le temps de tracé de la fonction f d'expression suivante, en mode radians :
Epsilon 23 | Epsilon 24 | |
NumWorks N0110/N0115 | 2.544s | 5.74s |
NumWorks N0120 | 0.357s | 1.396s |
Ici curieusement, évolution dans l'autre sens avec des tracés dans les 2 à 4 fois plus lents (possiblement liés au temps nécessaire pour déterminer automatiquement les bornes de la fenêtre graphique).
Pour le moment, les quelques améliorations apportées, notamment sur les sommes pour l'étude des séries numériques dans l'enseignement supérieur, sont très loin de compenser tout ce que l'on perd.
Rien de grave, NumWorks va sûrement redoubler d'efforts pour t'apporter un moteur de calcul pleinement fonctionnel pour une mise à jour Epsilon 24 stable d'ici les examens 2025... ou bien inversement faire preuve de sagesse/prudence et remettre ce changement majeur à une autre année.
Nous sommes juste un peu surpris qu'un moteur dans un tel état avec des anomalies dès le niveau Collège ait pu atteindre la phase de bêta-test public ; il y a tellement de dysfonctionnements dans tous les sens que nous voyons mal les utilisateurs sans aucun accès au code source pouvoir aider à mettre de l'ordre dans ce chaos.
À moins que les conséquences d'un des derniers changements apportés au moteur aient mal été évaluées...
Si la quasi totalité des régressions évoquées seront forcément corrigées par NumWorks d'une façon ou d'une autre (aucune inquiétude de notre part à ce sujet) ; nous ignorons toutefois si la possibilité d'effectuer du pseudo-calcul littéral sera conservée par le nouveau moteur de calcul.
Visiblement, ils étaient ces deux dernières années à fond sur une refonte intégrale de leur moteur de calcul, d'où l'impression de faiblesse des mises à jour que nous avons eue dans l'intervalle. Un projet majeur, consacrer autant d'énergie, de temps et d'une façon ou d'une autre de moyens à une telle tâche ne se fait pas sans objectifs à la mesure de la chose, d'autant plus lorsque le constructeur disposait déjà, et de loin comme nous avons vu, du meilleur moteur de calcul de tout le milieu de gamme graphique.
L'abandon comme nous avons supposé du traitement des expressions via des arbres de calcul devrait permettre d'économiser de la mémoire.
Comme redgl0w l'a évoqué, cela pourrait s'inscrire dans le projet du constructeur de sortir une calculatrice scientifique pour le Collège, qui n'aura pas d'autre choix que d'être proposée sous la barre des 30€ au grand maximum, et aura besoin d'un matériel choisi en conséquence possiblement avec moins de mémoire entre autres.
Sous cette hypothèse, les utilisateurs de la calculatrice NumWorks graphique seraient donc en train de bêta-tester le moteur de calcul de la future calculatrice NumWorks scientifique. Et une fois ce futur modèle sorti, on pourrait imaginer que calculatrices NumWorks graphique et scientifique partagent le même moteur de calcul, afin de mutualiser les forces de développement.
Regardons la chose sous un angle différent. Supprimer les arbres de calcul donc, mais pour les remplacer par quoi ?
Même si à ce jour il dysfonctionne, et mis à part le pseudo-calcul littéral sur lequel nous avons un doute, le nouveau moteur de calcul d'Epsilon 24 n'est en rien inférieur au précédent.
Cela reste un moteur avec des capacités de calcul exact très supérieures aux moteurs QPiRac de la concurrence.
Le projet n'était donc pas d'offrir un moteur inférieur pour satisfaire les conditions d'approbation de la NumWorks à des examens hors de France. De plus dans ce cas il n'y aurait absolument pas eu besoin de s'embêter à tout recoder ; de simples désactivations supplémentaires d'affichages pour certaines formes d'arbres-résultats auraient suffi.
Donc le nouveau moteur de calcul n'est plus un moteur de calcul exact par arbres, n'est pas davantage un moteur de calcul exact QPiRac et encore moins tout autre moteur inférieur... et si c'était en interne un moteur de calcul formel (ou CAS) ?...
Rien ne le prouve, mais si l'on exclut les algorithmes travaillant sur des arbres de calcul ainsi que les algorithmes numériques des moteurs inférieurs, il ne reste plus beaucoup de choix pour le sens du changement...
Un CAS peut-être donc, mais pour faire quoi, sachant que le moteur précédent permettait déjà du calcul littéral et que cette fonctionnalité était justement désactivée au niveau des résultats ?
C'est là justement que nous n'arrivons plus à voir bien clair, même si nous restons persuadés qu'il se trame quelque chose de gargantuesque. Tentons de ne pas passer à côté de la chose, voici plusieurs pistes en vrac :
- permettre grâce au CAS d'obtenir de meilleurs résultats numériques dans certains cas (même si nous n'avons pas réussi à trouver en dehors des grandes sommes jusqu'à présent)
- permettre de nouveau le calcul littéral et même formel sur calculatrices NumWorks lors d'une mise à jour future
- ou bien à la différence réserver le calcul littéral et formel à un futur modèle graphique haut de gamme qui partagera le même code source
- le moteur CAS pourrait même s'insérer également dans le cadre d'une refonte de la plateforme en ligne, permettant de rattraper le niveau de ce que proposent les concurrents
- viser l'approbation de la NumWorks en Allemagne pour la session 2030 de l'Abitur, le moteur CAS y étant obligatoire (mais il manquerait alors encore une application tableur, tout autant obligatoire)
- ou nuance, anticiper les changements de réglementation à venir dans l'un des pays ayant déjà approuvé la NumWorks, et qui serait tenté de s'inspirer de l'évolution de la réglementation allemande