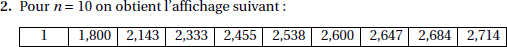[critor]

Les candidats au BAC S des lycées français du Liban ont démarré les épreuves avant-hier et ont passé les mathématiques hier.

Aucune correction complète n'étant visiblement disponible ce matin, après l'algorithmique puis l'exercice 1 dans deux news précédentes je viens de vous réaliser une correction de l'exercice 2 avec les probabilités conditionnelles mais aussi la loi normale, grosse nouveauté cette année.

En espérant que ce n'est pas trop tard pour ceux qui ont encore des DS aujourd'hui...




Liens:
Correction exercice n°2 du sujet de Maths du BAC S 2013 (Liban)
Sujets de Maths Obligatoire du BAC S 2013 (Liban)
Sujets de Maths Spécialité du BAC S 2013 (Liban)
Annales des sujets inédits du BAC S 2013 et corrigés

[critor]

Ce matin, les candidats au BAC S des lycées français du Liban ont eu droit à un algorithme en exercice 4 de leur sujet de Maths Spécialité. Certes, comme une majorité d'algorithmes du BAC il est posé dans le contexte d'une suite, mais c'est aussi notre premier algorithme de spécialité!

Alors jetons-y un coup d'oeil cette nuit sans plus attendre:

Question 1)
On sait donc que u₀=3 et u₁=8.
On en déduit que:
u₂=5*u₁-6*u₀=5*8-6*3=40-18=22
u₃=5*u₂-6*u₁=5*22-6*8=110-48=62



Question 2)a)
On veut donc un algorithme calculant le terme de rang n de la suite.

Il s'agit ici d'une suite récurrente d'ordre 2, c'est-à-dire que le calcul du terme suivant nécessite la connaissance des valeurs des deux termes précédents:
u_n+2=5u_n+1-6u_n

L'énoncé nous donne un algorithme à compléter
L'instruction de sortie finale 'Afficher b' nous indique que c'est la variable b qui contiendra à la fin le résultat voulu, et c'est justement l'instruction d'affectation de b qui manque dans l'algorithme.

On sait donc que u₂=22.

Tentons de réaliser une trace de l'algorithme dans le cas où n=2, avec les valeurs des variables à chaque instruction:
[tableborder=1]Instructionabcnia prend la valeur 33b prend la valeur 838Saisir n382Pour i=23822c prend la valeur a38322a prend la valeur b88322b prend la valteur ...822322[/table]

En dernière ligne de la trace, une affectation qui avec les valeurs courantes des variables reproduit le calcul 5*8-6*3 qui donne 22 est donc "b prend la valeur 5a-6c".
Notons qu'il y a une autre solution: "b prend la valeur 5b-6c", puisque a et b contiendront toujours la même chose au moment de cette instruction qui fait en effet suite à "a prend la valeur b".

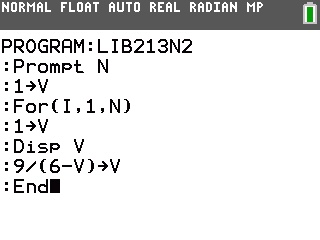
L'algorithme final peut donc être:

Code: Select all

Initialisation:
   a prend la valeur 3
   b prend la valeur 8
Traitement:
   Saisir n
   Pour i variant de 2 à n faire
      c prend la valeur a
      a prend la valeur b
      b prend la valeur 5a-6c
   Fin Pour
Sortie:
   Afficher b

Le sujet a la gentillesse de donner ce qu'est censé afficher l'algorithme.

En situation d'examen, afin de confirmer notre réponse avant de continuer il suffit de programmer l'algorithme sur notre calculatrice graphique et de vérifier qu'il donne les mêmes valeurs.

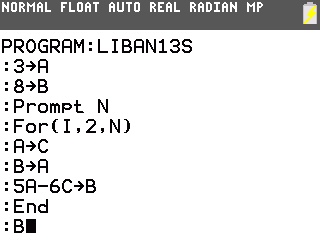
Voici le programme pour calculatrices TI-82 à TI-84:

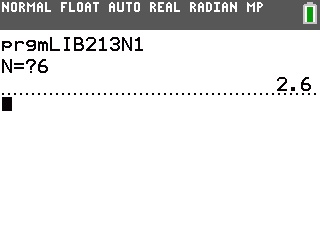
Voici maintenant ce qu'il affiche:

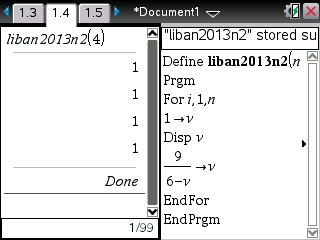
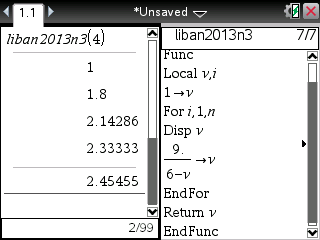
On constate bien des résultats cohérents avec l'énoncé ci-dessus.



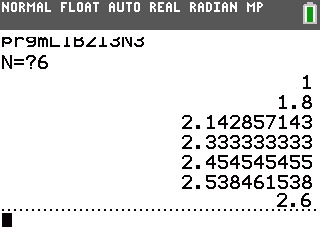
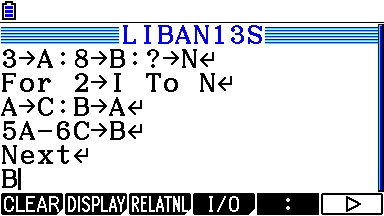
Si vous êtes munis d'une Casio Graph/Prizm, vous pouvez réaliser la même chose en saisissant le programme suivant:

Et voici son affichage, encore une fois cohérent:

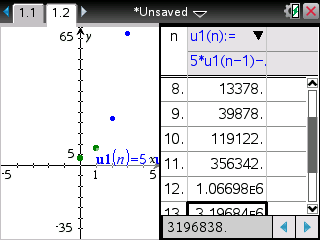
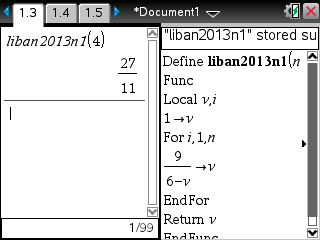
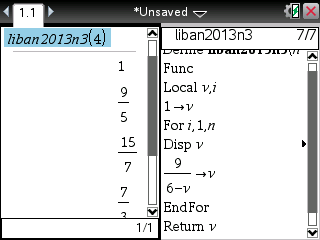
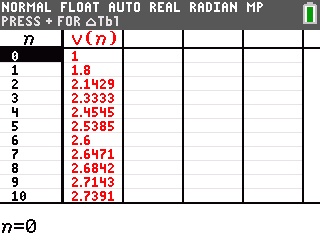
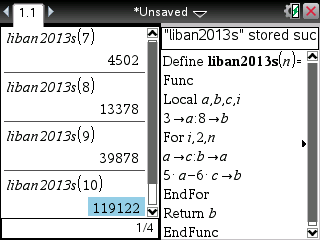
Si enfin vous êtes munis d'une TI-Nspire ou TI-89/92/V200, voici le programme et ses affichages une fois de plus cohérents:

Avant de nous quitter, posons-nous une dernière question au cas où...
Et si l'énoncé n'avait pas donné l'affichage correct de l'algorithme?

Il vous aurait suffi dans ce cas de définir la suite sur votre calculatrice et d'en demander un tableau de valeurs.

Sur TI-82 à TI-84, commencez par passer en mode 'suite' ou 'sequence' en anglais -

La suite vous est donc définie par une relation de récurrence u_n+2=5*u_n+1-6*u_n.

La calculatrice ne vous permet pas de définir le terme de rang n+2 (ni même n+1) mais uniquement le terme de rang n.

Vous devez donc commencer par réécrire cette relation deux rangs en-dessous, c'est-à-dire en remplaçant tous les 'n' par des 'n-2'.
Cela nous donne u_n=5*u_n-1-6*u_n-2

Une fois cette relation établie, il vous suffit d'aller la saisir -

Notons bien que dans le cas de cette suite récurrente d'ordre 2, il faut bien préciser dans une liste les deux valeurs initiales 3 et 8 dans l'ordre inverse de leur rang.

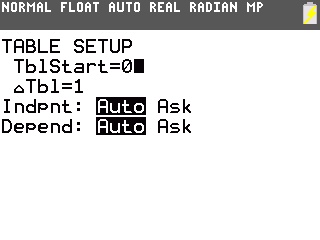
Selon l'état de votre calculatrice, il peut alors être nécessaire de modifier les paramètres du tableau de valeurs, à partir de 0 avec un pas de 1 dans le cas d'une suite -

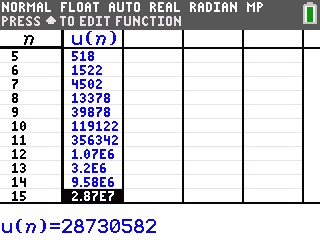
Et vous pouvez enfin demander le tableau de valeurs -

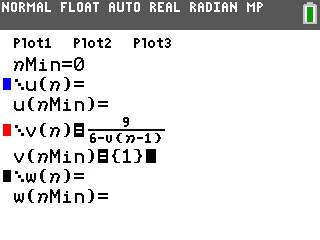
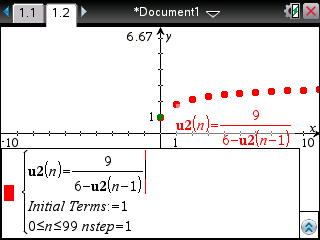
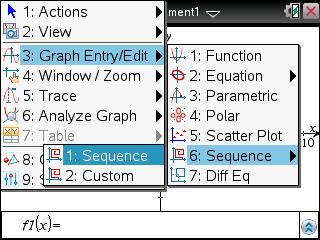
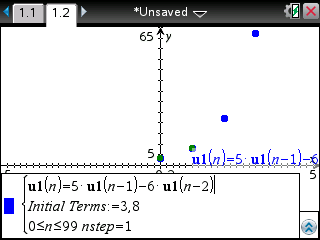
Sur TI-Nspire il vous faut utiliser la même relation.
Dans une application graphique, choisissez un entrée sous forme de suite -

Saisissez alors la relation trouvée plus haut:

Remarquons que contrairement aux TI-82 à TI-84, les termes initiaux sont ici à lister dans le même ordre que leur rang.

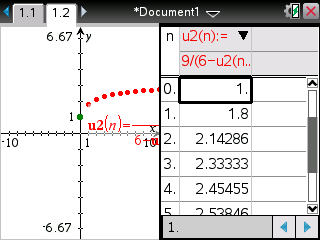
Et demandez enfin le tableau de valeurs -

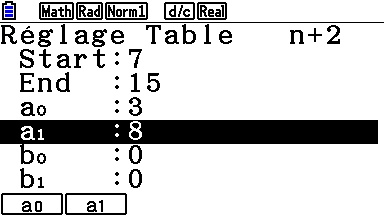
Sur une Casio Graph/Prizm, il suffit d'accéder à l'application 'Recurrence'.
L'application permet bien à priori de définir directement le terme de rang n+1, mais c'est le terme de rang n+2 qu'il nous faudrait ici...

En fait, c'est parfaitement possible - il suffit de changer la forme de saisie de la suite dans le menu [TYPE]:

L'on peut maintenant saisir directement l'expression de l'énoncé!

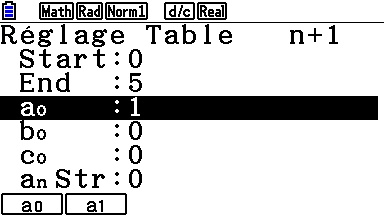
Mais il ne faut surtout pas oublier de préciser la valeur des termes initiaux, et cela se fait dans un autre écran accessible via le menu [SET]:

Une fois cet écran trouvé plus d'erreur possible, car les rangs des termes initiaux sont clairement indiqués!

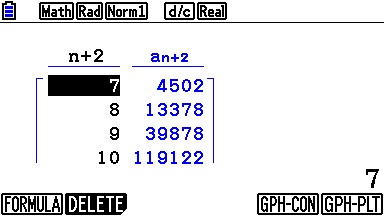
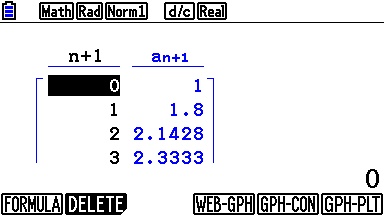
On y précise également les paramètres de notre tableau de valeurs, que voici enfin:

Lien:
Annales des sujets inédits du BAC S 2013 et corrigés

[critor]

Les candidats au BAC S des lycées français du Liban ont démarré les épreuves hier et ont passé les mathématiques ce matin.

Aucune correction complète n'étant visiblement disponible ce soir, après l'algorithmique dans une news précédente je viens de vous réaliser une correction de l'exercice 1 avec le QCM de géométrie dans l'espace.

Bien plus que les simples réponses, vous y avez le détail d'une stratégie possible, élément très important dans un QCM sans justification!

Dans l'urgence, cela pourra donc servir à ceux qui ont encore des derniers DS ou BAC blancs dans les tous prochains jours.




Liens:
Correction exercice n°1 du sujet de Maths du BAC S 2013 (Liban)
Sujets de Maths Obligatoire du BAC S 2013 (Liban)
Sujets de Maths Spécialité du BAC S 2013 (Liban)
Annales des sujets inédits du BAC S 2013 et corrigés

[critor]

Ce matin, les candidats au BAC S des lycées français du Liban ont sans surprise eu droit à un algorithme en exercice 4 de leur sujet de Maths Obligatoire, et comme une majorité d'algorithmes du BAC il est posé dans le contexte d'une suite.

Jetons-y un coup d'oeil ce soir:

Question A)1)
On veut donc un algorithme affichant tous les termes d'une suite v, du rang 0 au rang n.

On a la gentillesse dans ce sujet bien sympa de vous proposer 3 algorithmes déjà complets, et simplement de vous demander de choisir le bon.

L'algorithme 1 est à rejeter.
La seule instruction de sortie "Afficher v" arrive en effet après l'instruction "Fin pour". Elle est donc en dehors de la boucle et ne sera exécutée qu'une seule fois. Cet algorithme affichera dans tous les cas 1 seul terme et ne répond pas à la question posée.

L'algorithme 2 est également à rejeter.
L'instruction de sortie "Afficher v" fait suite à une instruction "v prend la valeur 1". Cet algorithme n'affiche donc que des 1 au lieu des valeurs des termes de la suite.

Par élimination, il ne reste donc que l'algorithme 3.





Notons que si vous avez du mal à lire/comprendre les algorithmes, il était également possible de trouver la réponse de façon empirique en utilisant la calculatrice graphique.

L'énoncé a la gentillesse (décidément) de donner en question A)2) ce qu'est censé afficher l'algorithme.

Il suffit donc de programmer les 3 algorithmes et de voir lequel produit le bon affichage.

Voici les 3 programmes pour calculatrices TI-82 à TI-84:

Voici maintenant leurs affichages respectifs:

On constate bien les comportements décrits plus haut.
On peut y ajouter une petite précision: l'algorithme 1 affiche bien un seul terme, et il s'agit du terme de rang n.



Si vous êtes munis d'une Casio Graph/Prizm, vous pouvez réaliser la même chose en saisissant les programmes suivants:

Et voici leurs affichages:

Pour le programme 2, l'affichage de 1.8 n'est déclenché par aucune instruction. C'est tout simplement la dernière valeur numérique utilisée dans le programme, que la calculatrice renvoie en tant que résultat, et notamment ici il s'agit de la dernière exécution de l'instruction d'affectation.



Si enfin vous êtes munis d'une TI-Nspire ou TI-89/92/V200, voici les programmes et leurs affichages:

On remarque que le programme 3 affiche des valeurs exactes fractionnaires pour v sur TI-Nspire CAS. Il suffit de provoquer le calcul de v en mode numérique et cela peut se faire par simple utilisation du séparateur décimal dans l'affectation de v:

Avant de nous quitter, posons-nous une dernière question au cas où...
Et si l'énoncé n'avait pas donné l'affichage correct de l'algorithme?

Il vous aurait suffi dans ce cas de définir la suite sur votre calculatrice et d'en demander un tableau de valeurs.

Sur TI-82 à TI-84, commencez par passer en mode 'suite' ou 'sequence' en anglais -

La suite vous est donc définie par une relation de récurrence v_n+1=9/(6-v_n).

La calculatrice ne vous permet pas de définir le terme de rang n+1 mais uniquement le terme de rang n.

Vous devez donc commencer par réécrire cette relation au rang inférieur, c'est-à-dire en remplaçant tous les 'n' par des 'n-1'.
Cela nous donne v_n=9/(6-v_n-1)

Une fois cette relation établie, il vous suffit d'aller la saisir -

Selon l'état de votre calculatrice, il peut alors être nécessaire de modifier les paramètres du tableau de valeurs, à partir de 0 avec un pas de 1 dans le cas d'une suite -

Et vous pouvez enfin demander un tableau de valeurs -

Sur TI-Nspire il vous faut utiliser la même relation.
Dans une application graphique, choisissez un entrée sous forme de suite -

Saisissez alors la relation trouvée plus haut:

Et demandez enfin le tableau de valeurs -

Sur une Casio Graph/Prizm, il suffit d'accéder à l'application 'Recurrence'.
Il est possible ici d'y définir directement le terme de rang n+1!

Mais il ne faut surtout pas oublier de préciser la valeur du terme initial, et cela se fait dans un autre écran accessible via le menu [SET]:

On y précise également les paramètres de notre tableau de valeurs, que voici enfin:

Lien:
Annales des sujets inédits du BAC S 2013 et corrigés

[critor]

Après le sujet de spécialité dans la news précédente, voici maintenant, à nouveau grâce à l'APMEP, le sujet de Mathématiques Obligatoire tombé ce matin pour les candidats au BAC S des lycées français du Liban.

Au menu:

• Exercice 1 (4 points): Un QCM sans justification et sans pénalité, et comme une majorité de QCM au BAC il porte sur la géométrie dans l'espace.
• Exercice 2 (5 points): Un problème de probabilités, touchant aux probabilités conditionnelles et aux lois normales qui sont une nouveauté cette année.
• Exercice 3 (6 points): Un exercice d'étude de fonction.
• Exercice 4 (5 points): Comme dans la version Spécialité du sujet, un exercice sur les suites - et c'est l'occasion là encore d'y caser un algorithme, une majorité des algorithmes au BAC tombant dans le contexte de suites.

A bientôt!

Lien:
Annales des sujets inédits du BAC S 2013 et corrigés