Pour cette rentrée 2024,
Casio sort une nouvelle calculatrice graphique couleur, la
Graph Math+, en remplacement de sa
Graph 90+E de rentrée 2017.
Nous avons eu accès à plusieurs exemplaires de la
Graph Math+ dans le cadre de la préparation de ce test.
Nous avons d'abord eu accès à un
SAMPLE de la
Graph Math+ (exemplaire non finalisé pouvant être qualifié de prototype), que nous étions allé tester chez
Casio début avril afin de gagner un peu de temps sur la préparation de ce test, mais que nous n'avions pas pu emporter. Il nous permettra toutefois de t'apporter quelques précisions.
Depuis,
Casio nous a fait l'honneur de nous envoyer un exemplaire finalisé de cette
Graph Math+ (merci ❤️), alors découvrons ensemble tout ce qu'elle cache sous le capot. C'est parti !

La
Graph Math+ vient dans un emballage carton, un emballage écologique ayant le gros avantage d'être réutilisable après ouverture !
La
Graph Math+ dans son emballage pèse
319g, contre
428g pour la
Graph 90+E emballée.


Pour la même épaisseur l'emballage
Graph Math+ est certes légèrement plus haut que celui de la
Graph 90+E, mais aussi beaucoup moins large.
Nous mesurons en effet pour l'emballage
Graph Math+ :
- 3,27 cm d'épaisseur
- 9,43cm de largeur (contre 14,39cm pour l'emballage Graph 90+E)
- 22,74cm de hauteur utile (contre 19,50cm pour l'emballage Graph 90+E)

Il est maintenant temps d'ouvrir l'emballage.
À ce sujet, les emballages carton de
Casio avaient un petit problème. Naturellement, nombre de personnes trouvaient cela normal de les ouvrir par le haut, c'est-à-dire ici par la partie permettant de les suspendre en rayon. Sauf que les ouvrir proprement de ce côté est assez technique, avec un assemblage de pas moins de 4 épaisseurs de carton. Le plus souvent on abîmait plus ou moins sérieusement l'emballage, ce qui donnait moins envie de le conserver.
Avec la
Graph Math+ et sans doute tous les nouveaux emballages carton de l'ensemble des calculatrices
Casio pour cette rentrée 2024,
Casio a prévu quelque chose par rapport au problème précédent. L'autocollant scellant la partie inférieure de la boîte s'est vu rajouter une inscription on ne peut plus claire en Français :
OUVERTURE. Un souci du détail qui devrait aider à ce que moins d'élèves peinent à ouvrir les boîtes
Casio du mauvais côté.

Ouvrons donc l'emballage afin de trouver la raison de cette perte significative à la fois en masse et en volume.
Nous y trouvons :
- la calculatrice avec sa coque, soigneusement protégées sous papier bulle
- le guide de démarrage rapide
- le dépliant d'information sur la garantie (3 ans) et le recyclage
- 4 piles AAA de chez Toshiba, prêtes à être installées
- ... et puis c'est tout
La question est donc surtout de savoir ce que l'on n'y trouve pas. Et effectivement il n'y a plus les câbles de connectivité, que ce soit le câble
USB pour ordinateur ou le câble de transfert entre calculatrices pour le port historique
mini-Jack 2.5mm. Des câbles qui certes ne pesaient pas grand chose à eux seuls, mais nécessitait des éléments d'emballage supplémentaires afin de les caler correctement. Nous ne manquerons pas de traiter justement de la connectivité plus loin.
A2) Boîtier, alimentation et ports connexionGo to top 
Prenons donc la
Graph Math+ en main. Nous mesurons :
- 8,85cm de largeur dans tous les cas (contre pour la Graph 90+E 8,93cm sans la coque et 9,56cm avec la coque, ou 7,70cm pour la fx-92 Collège Classwiz )
- 19,86cm de hauteur avec coque (contre 18,89cm pour la Graph 90+E, ou 18,87cm pour la fx-92 Collège Classwiz)
- 18,77cm de hauteur sans coque (contre 18,89cm pour la Graph 90+E, ou 17,72cm pour la fx-92 Collège Classwiz)
- 2,56cm d'épaisseur avec coque (contre 2,53cm pour la Graph 90+E, ou 2,10cm pour la fx-92 Collège Classwiz)
- 2,06cm d'épaisseur sans coque (contre 2,04cm pour la Graph 90+E, ou 1,55cm pour la fx-92 Collège Classwiz)
- 265g avec coque (contre 282g pour la Graph 90+E, ou 155g pour la fx-92 Collège Classwiz)
- 223g sans coque (contre 227g pour la Graph 90+E, ou 119g pour la fx-92 Collège Classwiz)
Notons au passage aussi bien sur la coque qu'au dos d'ailleurs, de nouveaux patins antidérapants en croisillons. Espérons qu'ils seront ainsi plus durables que les patins ronds de la
Graph 90+E qui finissaient toujours pas se détacher et souvent se perdre, et ce malgré tout le soin dont nous savons faire preuve avec nos calculatrices.

Bref, la
Graph Math+ a donc des dimensions assez similaires à celles de la
Graph 90+E. Toutefois, les coques n'utilisent pas le même système de verrouillage :
- coque coulissante pour Graph 90+E
- coques à clipser pour Graph Math+
Il ne sera donc pas possible d'échanger tes coques entre les
Graph 90+E et
Graph Math+, précision importante si tu disposais d'une édition limitée de la coque
Graph 90+E. La coque
Graph 90+E ne pourra pas s'insérer complètement et donc se verrouiller sur
Graph Math+, et inversement la coque
Graph Math+ ne pourra pas tenir en place sur
Graph 90+E.

D'un autre côté les coques
Graph Math+ et
fx-92 Collège Classwiz utilisent certes le même système de verrouillage. Toutefois, les dimensions étant différentes, elles ne seront ici aussi malheureusement pas interchangeables, précision importante si tu disposais d'une édition limitée de la coque
fx-92 Collège Classwiz.
Contrairement à la concurrence couleur, pas de batterie rechargeable ici. La
Graph Math+ s'alimente donc par un bloc de 4 piles
AAA mises en série, c'est-à-dire sous
6 Volts. Ce n'est pas forcément un point faible ; tout est question de point de vue. Nos tests montrent qu'à matériel et donc consommation similaire, l'autonomie de bonnes piles
AAA est nettement supérieure à celle des batteries Lithium-ion que les concurrents préinstallent dans leurs modèles, et ce même en testant contre des batteries neuves complètement chargées. Installons donc vite les 4 piles
Toshiba fournies :
Le numéro de série
C875A3C001748AE_40 présent sur l'autocollant à code barre dans le compartiment d'alimentation utilise un nouveau format que
Casio a introduit pour la rentrée 2022, et qui malheureusement est loin d'être entièrement compris à ce jour.

En incluant le prototype testé chez
Casio début avril, petit échantillon des numéros de série
Graph Math+ récupérés à ce jour :
- Code: Select all
C875A1C000144ZZ_44 #sample
C875A3C001746AE_40 #échantillon Lephe
C875A3C001747AE_40 #échantillon Adriweb
C875A3C001748AE_40 #échantillon Critor
On y trouve la référence du modèle
CY875AC, scindée en deux parties avec d'une part les 5 premiers caractères, et d'autre part le 7
e caractère.
Une référence similaire
CY875AR8 était également présente sur le prototype, via au dos l'étiquette
MS (Marketing Sample) caractéristique des exemplaires
Casio non finalisés. L'étiquette était de plus datée en format japonais,
24年3月4日, correspondant au
4 mars 2024. C'est bien évidemment la date de l'étiquetage, forcément ultérieure à la date d'assemblage du prototype en question.
Revenons à nos numéros de série, le 6
e caractère indique ici le mois de production, avec comme dans l'ancien format utilisé jusqu'en 2021 :
- 1 à 9 pour janvier à septembre
- X, Y et Z pour octobre, novembre et décembre
Le prototype avait donc été assemblé en
Janvier 2024, et l'exemplaire finalisé que nous te présentons aujourd'hui en
Mars 2024.
Nous disons 2024 parce qu'il n'y a aucun doute possible cette année. Mais contrairement à l'ancien format utilisé jusqu'en 2021, l'année d'assemblage ne semble pas présente dans le nouveau format, ou du moins pas en clair.
Les 6 caractères suivants, constituent la partie numérique du numéro de série, c'est-à-dire croissante en fonction du temps jusqu'à la prochaine remise à zéro.
Et le suffixe restant avec 2 lettres suivies d'un séparateur puis de 2 chiffres nous reste hélas totalement obscur à ce jour.
Pour ceux qui se sentiraient capables de nous aider à
"casser le codage", ou trouveraient simplement cette activité amusante, un échantillon plus large de ces nouveaux numéros de série couvrant des exemplaires d'autres modèles sortis d'usine depuis 2022, est disponible
sur MyCalcs.


Regardons un petit peu la tranche supérieure de la calculatrice. Niveau connectivité nous avons une excellente nouvelle à t'apprendre. La
Graph Math+ abandonne enfin le port
mini-USB pour lequel les élèves et enseignants avaient de moins en moins souvent la bonne connectique sous la main en cas de besoin, au profit d'un port
USB-C !
Enfin donc un port de connexion moderne, pour lequel la connectique nécessaire sera le plus souvent disponible à portée de main, et qui plus est au format
USB-C, un format de connecteur réversible ayant l'immense avantage de permettre de brancher le câble les yeux fermés ! 👍
Le port série historique
mini-Jack 2.5mm est pour sa part conservé.
On peut noter au passage que les positions des ports
USB et série sont inversées sur
Graph Math+ par rapport à la
Graph 90+E ainsi que tous les modèles
Casio sortis jusqu'ici.
A3) Esprit de la nouvelle interface par ongletsGo to top 
L'interface
Graph 90+E n'était en fait qu'une version colorisée, agrandie et décorée de celle de la calculatrice
Graph 35+E II monochrome. On retrouvait très exactement les mêmes écrans et menus, à un point de similarité tel que la
Graph 35+E II pouvait être qualifiée de photocopie monochrome de la
Graph 90+E.
Pour
Casio cela simplifiait probablement les choses. L'interface était sans doute conçue et peut-être même codée une seule fois, avant d'être par la suite compilée soit en version couleur soit en version monochrome.
Toutefois, les écrans avaient des définitions différentes :
128×64 pixels pour
Graph 35+E II, contre
396×224 sur
Graph 90+E.
Pour remplir cet objectif de similarité des interfaces et menus malgré cela, la
Graph 90+E utilisait une police de caractères ridiculement énorme, lui permettant de faire rentrer à l'écran très exactement les mêmes nombres de lignes et colonnes de caractères que la
Graph 35+E II, et pas un seul de plus. C'est donc un choix de grossissement par 3 des dimensions de l'ensemble des objets graphiques qui très clairement avait fort tristement bridé tout ce qu'il était possible de faire avec la formidable définition en
396×224 pixels de l'écran
Graph 90+E.
Les polices
Graph 35+E II et
Graph 90+E permettaient d'afficher
7 lignes de
21 colonnes, comme on peut mesurer à l'écran de calcul ou dans un éditeur de fichier. Et toutes les interfaces des différentes applications respectaient strictement ce découpage de l'écran puisqu'utilisant la même police peu importe le contenu affiché.
Un autre point faible de la
Graph 90+E concernait les menus de bas d'écran te présentant les actions disponibles dans les diverses applications. On pourrait les qualifier d'onglets
matériels car chacun était lié à l'une des touches de fonction
F1
à
F6
du clavier physique, contraignant donc leur nombre et position.
Quand j'étais petit, j'adorais ce système du point de vue programmeur. Même si cela existait déjà, je l'ai découvert sur ma première calculatrice graphique en classe de Troisième en 1992-1993, la
TI-85 sortie elle-même pour la rentrée 1992. Et en effet pour créer des programmes c'était hyper pratique, un appel simplissime à une commande
Menu() d'une seule ligne suffisant à afficher un menu discret et fonctionnel avec tout ce que l'on voulait en bas d'écran, sans avoir donc à se préoccuper de calculer les positions des différents cadres de pixels à afficher, tout en laissant l'ensemble du reste de l'écran libre pour visualiser simultanément à l'utilisation du menu tout ce que l'on voulait
(contexte d'appel avec par exemple les éléments définis au sein du programme, comme par exemple les suites numériques puisque la TI-85 avait le défaut de ne pas les gérer, représentation graphique des éléments définis dans le programme, détail des différentes éléments du menu ou bien aide à l'utilisation plus générale, dessin de décoration ou logo du programme, titre et nom de l'auteur du programme, etc.). 1 seule ligne pour un menu complet, et l'on pouvait donc se concentrer sur la programmation de l'essentiel, c'est-à-dire des fonctionnalités du programme en question.
Depuis j'ai eu la chance de pouvoir adopter d'autres points de vue, dont le point de vue enseignant m'amenant à dire que si cette présentation me convient toujours parfaitement, elle n'est pas toujours l'idéale pour les élèves.
Pas de problème d'intuitivité ici, chaque touche située sous l'écran correspondant exactement à la position de l'affichage de l'onglet en bas d'écran, le problème est ailleurs.
Ces onglets étant donc contraints par le matériel, leurs dimensions ne pouvaient varier. Ils occupaient ainsi toujours en largeur 1/6 de celle de l'écran, ce qui ne laissait pas beaucoup de place pour y décrire leur action, surtout avec le choix de police que nous venons d'évoquer, ainsi qu'avec un biseau rajouté sur les onglets ouvrant de sous-onglets, laissant encore moins d'espace disponible. Tout ceci forçait
Casio à inscrire dans ces onglets des abréviations, pas toujours claires aux yeux des élèves, surtout lorsqu'en prime les abréviations étaient basées sur de l'anglais aux mots bien souvent plus courts et donc plus faciles à abréger.
Autre problème constaté en classe, bien souvent pour les manipulations les élèves ne tentaient pas de retenir les noms d'onglets à actionner, mais les touches à presser soit
F1
à
F6
. Une façon de faire faisant perdre tout le sens de la manipulation, et qui ainsi ne rendait la chose que plus difficile à retenir, et il fallait donc régulièrement leur répéter comment faire.
Avant même de passer par l'écran d'accueil de la
Graph Math+, nous allons te présenter en quelques mots l'esprit de la nouvelle interface car cela va être bien important pour mieux comprendre tout ce qui va suivre et saisir tout ce qui a été fait.
Déjà, rappelons que dans l'univers des calculatrices graphiques nous n'avions plus eu droit à de nouvelles interfaces depuis 2017. C'est donc un geste majeur et surtout courageux de la part de
Casio.
Avec la
Graph Math+, nous partons littéralement vers de tout nouveaux horizons. C'est ici toute l'interface qui a été repensée, ne ressemblant a priori à rien de connu, une interface donc conçue désormais sans aucune contrainte ! Il est maintenant grand temps de la découvrir.

Un changement majeur concerne les onglets de bas d'écran. Nous n'avons plus que 2 onglets affichés, même si davantage d'onglets peuvent toujours être disponibles. Cela permet d'avoir beaucoup plus de place pour les décrire explicitement, plus besoin d'abréviations !
Mais avant d'aller plus loin nous nous devons de te préciser quelque chose d'essentiel ; ces onglets n'ont plus rien à voir avec ce que tu as connu sur les graphiques
Casio depuis le siècle dernier. Avec la
Graph Math+ il y a en effet un changement radical de philosophie à leur sujet.
Sur
Graph 90+E, les onglets de bas d'écran servaient à saisir/déclencher des actions, éventuellement en passant par des sous-menus d'onglets. Sur
Graph Math+ à la différence, ils sont exclusivement dédiés à basculer entre différentes vues
(on pourrait dire aussi écrans ou pages) de l'application courante. A priori un changement hautement pertinent permettant aux élèves de mieux acquérir la compétence
Représenter !
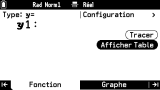
Quant aux actions, puisqu'elles semblent désormais totalement absentes des onglets de bas d'écran il faut bien les mettre quelque part. Nous avons à cette fin quelques boutons dédiés aux actions qui apparaissent au sein même des interfaces des différentes vues, et qui se sélectionnent simplement avec les flèches du clavier.
L'interface a également tendance à laisser autant que possible visible le contexte d'appel, notamment par :
- la superposition d'une ou même plusieurs fenêtres popup pour les appels d'interfaces, menus ou saisies, en lieu et place d'un affichage plein écran
- une aide en ligne discrète dans la barre de titre
- la table des caractères spéciaux dont l'interface lorsque appelée prend la place des onglets de bas d'écran, au lieu ici encore d'un affichage plein écran
- des icônes flottantes notifiant certains événements
Tout ceci partage un même et unique but. Un avantage scolaire est en effet de ne plus couper brutalement et totalement l'utilisateur du contexte d'appel par des affichages plein écran dans ces cas-là, le contexte restant donc
(partiellement) visible à l'écran ! 👍
Rajoutons à cela divers signes visuels dans les différents onglets d'application invitant par exemple :
- à taper la flèche vers la droite pour ouvrir un menu déroulant sur un choix d'option
- à taper la touche de menu contextuel, que nous allons te présenter de suite, afin d'offrir davantage de possibilités pour l'objet sélectionné
Nous allons bientôt t'illustrer ce que donne tout ceci avec les diverses applications intégrées. Et cela va être également l'occasion de voir que
Casio est très loin de s'être contenté des ces aspects transversaux, mais a également fait des choses spécifiques au moins pour certaines de ces applications.
Mais attention car l'intuitivité ne fait pas tout.
Une interface, aussi claire, compréhensible et intuitive soit-elle, se doit également d'être agréable et simple d'utilisation. Et comme nous n'avons pas ici d'écran tactile, cela relève grandement de choix effectués au niveau du clavier.
Alors regardons plus en détails le clavier sans plus attendre...
A4) Principe du clavier et équivalents hors de FranceGo to top 
Le clavier de la
Graph Math+ n'a plus grand chose à voir avec celui de la
Graph 90+E. Il reprend et fait évoluer en fait celui introduit avec la
fx-92 Collège Classwiz de rentrée 2023 avec sa nouvelle organisation en 48 touches.
Rappelons l'esprit de l'organisation en question, car cela va être essentiel pour mieux comprendre la suite.
Déjà, première chose qui saute aux yeux lors d'un passage de la
Graph 90+E à la
Graph Math+, les touches de fonction historiques
F1
à
F6
disparaissent dans le cadre de la toute nouvelle interface par onglets que nous venons de te présenter.
Et comme nous n'avons pas d'écran tactile, c'est que nombre de choses vont désormais nécessiter l'utilisation des touches fléchées et validation.
C'est notamment le cas des onglets qui n'étant plus liés à des touches de fonction deviennent donc ici des onglets purement logiciels, n'étant plus contraints à 1/6 de la largeur de l'écran et pouvant désormais adopter n'importe quelle largeur comme nous avons vu ! 👍
La
Graph 90+E disposait de 2 touches moins au clavier :
(-)
pour le moins de signe-
pour le moins de soustraction
La distinction est importante, ce sont 2 objets mathématiques complètement différents, l'un étant une fonction à 1 argument en écriture préfixée, et l'autre une fonction à 2 arguments en écriture infixée.
Mais au collège puis au lycée, on n'enseigne pas à les différentier, utilisant le même symbole pour les deux.
En pratique pas de risque d'erreur pour les élèves, car
Casio avait déjà très bien travaillé et mis de l'intelligence dans son moteur de calcul :
- si on tapait
-
pour un signe en début de saisie dans un bloc ou juste après avoir ouvert une parenthèse, aucune ambiguïté possible puisqu'1 seul argument, et ça marchait quand même - et si on tapait
(-)
pour une soustraction, il y avait ambiguïté possible puisque 2 arguments, et nous obtenions une erreur
Toutefois, 2 touches moins mises en avant de façon similaire au clavier était perturbant pour les élèves, surtout qu'à la différence de
-
,
(-)
ne pouvait servir qu'en tant que signe.
Et bien justement, on peut noter sur
Graph Math+, un changement de mise en avant du moins de signe, passant d'une fonction principale de touche sur
Graph 90+E à une fonction secondaire de la touche
-
sur
Graph Math+.
La suppression de la touche moins de signe semble indique que
Casio semble faire de plus en plus confiance au fonctionnement fort intelligent que nous venons de te décrire.
Revenons à nos touches fléchées, suite à la suppression des touches de fonction. Un changement radical et également un risque de confier tant de choses aux flèches clavier, car nous pouvons reprocher nombre de choses à divers modèles anciens ou concurrents, dont certains sont même toujours d'actualité :
- commençons par les problèmes qui existaient entre autres sur Graph 90+E :
- positionnement du pavé directionnel souvent à droite, ce qui embête les gauchers et gauchères à devoir donc passer leur main par-dessus le clavier à chaque fois qu'une touche fléchée est nécessaire, masquant ainsi l'ensemble du clavier et gênant l'anticipation des touches à presser par la suite
- le pavé directionnel regroupant les touches fléchées est parfois constitué d'un seul bloc ce qui est d'une part moins agréable à presser qu'une touche isolée, il n'est pas rare que la pression d'une direction déclenche également accidentellement la pression d'une direction voisine, particulièrement embêtant sur les vues graphiques ainsi que pour les jeux
- et inversement, dans le cas d'un pavé directionnel d'un seul bloc, il est souvent plus difficile de maintenir une double pression pour indiquer les directions en diagonale
- ajoutons à cela la distance parcourue par les doigts, notamment pour aller du pavé directionnel à la touche de validation tout en bas à droite
- et voici maintenant les problèmes qui ne concernaient que d'autres modèles plus anciens ou concurrents :
- des touches fléchées qui ne sont pas positionnées de façon intuitive selon les directions qu'elles indiquent, mais de façon alignée en rangée et en colonne avec les touches adjacentes du clavier
- l'usure des touches, avec à force de pressions des touches qui finissent par moins bien réagir
- ou encore, à force de pressions des touches qui voient leurs inscriptions s'effacer
Dans le cas où comme ici suite à la disparition des touches de fonctions, le pavé directionnel devient un élément essentiel à l'ensemble des manipulations, les problématiques que nous venons de citer n'en deviennent qu'encore plus essentielles à prendre en compte.

Et bien
Casio, fort de sa riche expérience puisqu'ayant inventé la calculatrice graphique avec la
fx-7000G dès 1985, et faisant preuve de son sérieux habituel, semble en fait déjà avoir pris en compte la plupart des points précédents dès la
fx-92 Collège Classwiz de rentrée 2023.
La
fx-92 Collège Classwiz dispose en effet d'un pavé directionnel centré horizontalement, convenant donc à la fois aux droitiers et aux gauchers !
Ce pavé directionnel se compose de plus de plusieurs touches indépendantes, orientées intuitivement selon leurs directions respectives, et offrant donc le meilleur confort d'utilisation !
Dans le but d'alléger grandement le nombre de pressions sur les touches fléchées afin d'aller chercher le bon élément à l'écran ou bien encore hors écran
(notamment pour les menus), nous avons droit au pavé directionnel à 2 touches supplémentaires fléchées verticalement, permettant de faire défiler l'affichage d'une hauteur d'écran, vers le haut ou vers le bas, exactement comme sur le clavier d'un ordinateur ! 👍
Dans le but d'alléger également la distance parcourue par les doigts et donc la fatigue musculaire alors que ces derniers passent une grande partie de leur temps sur les touches fléchées, nous avons droit non pas à 1 mais à 2 touches de validation :
- l'habituelle touche de validation
EXE
en bas à droite, qui sera rapidement accessible en fin de saisie d'un calcul sur le pavé numérique - et une nouvelle touche de validation
OK
au centre du pavé directionnel, qui pour sa part sera littéralement sous la main pour valider immédiatement une sélection après navigation avec les les touches fléchées (notamment pour les boutons à actionner ou menus)


Pour le reste, le clavier
fx-92 Collège Classwiz réutilisé sur
Graph Math+ offre des touches pouvant avoir plusieurs fonctions :
- une fonction principale
- une fonction secondaire accessible via le modificateur
SECONDE
(renommé SHIFT
sur Graph Math+) - sur Graph Math+ uniquement, une fonction alphabétique accessible via le modificateur
ALPHA
À des fins d'allègement, de simplicité et d'intuitivité, plusieurs touches importantes ne présentent pas de fonction secondaire. Parmi elles on compte entre autres les touches fléchées dont nous venons de parler, mais aussi plusieurs autres touches dites transversales, faisant toute la supériorité du clavier de la
fx-92 Collège Classwiz :
ACCUEIL
, renommée HOME
sur Graph Math+, pour l'écran de sélection des applicationsCONFIG
, renommée SETTINGS
sur Graph Math+, pour le réglage des différents paramètresCATALOG
pour l'accès par catégories à l'ensemble des fonctions transversales intégrées à la calculatrice, ainsi qu'aux fonctions spécifiques à l'application courante...
(ou OUTILS, renommé TOOLS sur Graph Math+) pour ouvrir un menu contextuel offrant des manipulations spécifiques à l'application couranteVARIABLE
pour l'accès à un gestionnaire de variablesFORMAT
pour changer la forme d'affichage du dernier résultat
En effet comme tu peux voir, les inscriptions de touches sont en Anglais sur
Graph Math+, et non pas en Français comme sur
fx-92 Collège Classwiz. Cela indique qu'à la différence la
Graph Math+ est un modèle qui sera décliné à l'international.
Rappelons que la
Graph 90+E était un modèle commercialisé exclusivement en France. Il n'en restait pas moins qu'il disposait d'équivalents hors de nos frontières :
- à l'international la fx-CG50
- en Australie la fx-CG50AU
De la même façon, ce sont en fait 3 nouveaux modèles couleur similaires que
Casio s'aprête à nous lancer de par le monde :
- en France la Graph 90+E de rentrée 2017 est remplacée par la Graph Math+ dès cette rentrée 2024
- à l'international, la fx-CG50 de rentrée 2017 sera remplacée par la fx-CG100, mais probablement pas avant la rentrée 2025
- en Australie, la fx-CG50AU de rentrée 2018 sera remplacée par la fx-1AU GRAPH, mais probablement pas avant la rentrée 2025
Nous notons toutefois quelques toutes petites différences entre les claviers
fx-92 Collège Classwiz et
Graph Math+ :
- mise en valeur de la fonction secondaire d'extinction OFF sur la touche
AC
- le séparateur décimal passe de la virgule au point, et la touche
,
est donc remplacée par .
- par conséquent le séparateur d'arguments passant du point virgule à la virgule
- la touche
;
n'est donc plus nécessaire et est remplacée par l'exponentielle indispensable au lycée, avec les logarithmes rajoutés en fonctions secondaires sur les emplacements vides de la même rangée du clavier - la touche
Rép
permettant d'invoquer le dernier résultat disparaît, cédant la place à ,
pour le séparateur d'arguments - l'invocation du dernier résultat est déplacée en fonction secondaire de la touche
FORMAT
- nombre complexe i accessible en fonction secondaire de la touche
9
- la touche
f(x)
disparaît, puisque remplacée par le modificateur ALPHA
dont nous avons traité plus haut - séparateur de la forme polaire des nombres complexes accessible en fonction secondaire de la touche
8
- La division euclidienne en fonction secondaire de la touche
÷
disparaît ici - notations usuelles des variables de fonctions polaires accessibles en fonctions secondaires des touches
1
et 2
Traitons d'un ajout très important. Plusieurs fonctions secondaires caractéristiques de la
Graph 90+E sont reprises ici sur la rangée inférieure du clavier, mais cette fois-ci indiquées avec des icônes plutôt que des inscriptions.
Nous retrouvons entre autres la capture d'écran dont nous traiterons plus loin, mais également de quoi réaliser des
couper-coller ou
copier-coller, comme sur le clavier complet d'un ordinateur !
Pour réaliser un
couper-coller ou
copier-coller dans tout champ de saisie avec curseur de texte, rien de plus simple. Il te faut :
- taper
SHIFT
0
pour démarrer une sélection à la position du curseur - étendre alors la sélection à l'aide des touches fléchées
- valider la sélection (
EXE
ou OK
) - choisir alors entre couper et copier
- amener le curseur à l'endroit où coller la sélection mémorisée
- et enfin taper
SHIFT
.
pour coller
Une interface non tactile contrôlée intuitivement avec les flèches clavier, cela n'a rien de compliqué, n'importe qui peut en faire.
Mais dans le cadre d'une interface par onglets, supprimer les touches de fonction pour tout faire avec les touches fléchées, notamment les changements d'onglets, est une très mauvaise idée si l'on n'adapte pas le clavier en conséquence.
On peut citer en ce sens un certain modèle concurrent où les changements d'onglets sont assez pénibles, nécessitant :
- d'interrompre ce que l'on était en train de faire avec de possibles effets de bord
- pour avec une série plus ou moins longue de pressions de touches fléchées selon la position de l'élément sélectionné à l'écran, amener la sélection sur la barre d'onglets tout en haut de l'écran (ou tout en bas selon le modèle)
- quelques pressions de touches fléchées supplémentaires pour sélectionner le bon onglet dans la barre d'onglets
- et en prime la nécessité de presser la touche validation
Qu'est-ce que cela peut être lourd...


Et bien un véritable expert comme
Casio ne commet bien évidemment pas cette erreur.
Si tu regardes bien, par rapport à la
fx-92 Collège Classwiz, le pavé numérique de la
Graph Math+ dispose de 2 touches supplémentaires fléchées horizontalement.
Et bien voilà, les 2 touches en question permettent justement de passer à l'onglet suivant ou précédent. Aucun besoin ici d'interrompre ce que l'on faisait pour aller chercher la barre d'onglets possiblement à l'autre extrémité de l'écran, y sélectionner le bon onglet et en prime valider… une simple et unique pression de touche fait l'équivalent de tout cela, c'est génial ! 👍
Plus précisément, ces 2 touches additionnelles sont donc ici l'équivalent des raccourcis clavier
Shift+Tabulation et
Contrôle+Tabulation sur ordinateur.
Pour conclure, quelques détails de différences donc, mais les claviers
fx-92 Collège Classwiz et
Graph Math+ restent extrêmement similaires, partageant à la fois la même organisation et le même esprit. Après avoir utilisé la
fx-92 Collège Classwiz au collège, la prise en main de la
Graph Math+ par un lycéen ou une lycéenne n'en sera que grandement facilitée et accélérée ! 👍
A5) Ecran d'accueil, applications disponibles et manquantesGo to top 

Allumons enfin la
Graph Math+. Nous arrivons à l'écran d'accueil listant les applications disponibles.
Première impression par rapport à la
Graph 90+E,
Casio semble ici avoir fait le choix d'un
design autrement plus épuré pour la
Graph Math+. L'écran d'accueil met en effet beaucoup moins en avant les capacités couleur de l'écran, se contentant d'afficher les icônes d'applications en 4 teintes
(du noir, du blanc, des variantes de rouge, des variantes de bleu). Cela rappelle d'ailleurs très fortement la
fx-92 Collège Classwiz, qui utilisait 4 niveaux de gris pour les icônes d'applications sur ce même écran
(noir, blanc, gris clair, gris foncé).
Regardons maintenant rapidement ce qui est disponible niveau applications. Nous comptons
11 applications intégrées sur
Graph Math+, avec quelques changements ou ajouts :
- Sur la Graph 90+E, tout ce qui concernait les fonctions étaient disponible dans plusieurs applications différentes, 3 applications intégrées adjacentes (Graphe, G-dynamique et Table) ainsi qu'une application additionnelle (Plot Image). La Graph Math+ semble pour sa part fusionner tout ou partie de ces fonctionnalités au sein d'une seule et unique application, Graph&Table ! 👍
- Une toute nouvelle application Base-N dédiée aux calculs dans différentes bases numériques ! 👍
- L'application Système semble pour sa part renommée en Paramètres.
- Une toute nouvelle application Mode examen 👍
Mais si tu as bien compté jusqu'ici, en fait il nous manque pas mal d'applications sur
Graph Math+ par rapport à une
Graph 90+E.
Là où la
Graph 90+E présentait de 19 à 24 applications
(selon si l'on compte ou pas les applications additionnelles officielles préinstallées en usine en plus des applications intégrées), la
Graph Math+ ne présenterait donc plus que 11 applications à ce jour.
Si la réduction s'explique en petite partie par des fusions d'applications
(comme par exemple Graphe et Table qui deviennent Graphe&Table), c'est très loin de justifier un tel écart.
Nous nous inquiétions donc également de plusieurs manques. Aucune trace, du moins sur l'écran d'accueil
Graph Math+ précédent, de fonctionnalités
Graph 90+E plus ou moins importantes.
Déjà il manquerait, a priori, toutes les fonctionnalités offertes sur
Graph 90+E via les applications additionnelles officielles préinstallées en usine :
- application Physium pour le tableau périodique des éléments chimiques et la bibliothèque de constantes physiques
- application Graphe 3D pour les représentations dans un repère 3D de différents types d'objets (droite, plan, sphère, cylindre, cône)
- application Sim prob pour le simulateur d'expériences aléatoires
- application Géométrie pour la géométrie dynamique
- application Plot Image pour la superposition de tracés de graphes sur une image
Mais nous notons également des absences remarquées par rapport aux applications intégrées sur
Graph 90+E :
- application Tableur pour les feuilles de calcul
- application Programme pour l'édition et utilisation de programmes dans le langage interprété historique Casio Basic
- application G-dynamique pour l'animation des graphes de fonctions paramétrées
- application G-conique pour les représentations graphiques de fonctions coniques
- application Lien pour le transfert de données entre calculatrices
- application eActivity pour l'édition de documents scientifiques
- application E-CON4 pour l'acquisition de mesures physiques
- application Finance pour les calculs financiers
Casio a communiqué là-dessus. Plusieurs de ces fonctionnalités majeures seront rajoutées dans le cadre d'une mise à jour majeure
(peut-être donc déjà une version 2.00) qui sortira au premier semestre 2025.
Cette mise à jour offrira :
- des fonctionnalités équivalentes aux applications Graph 90+E intégrées Tableur et G-conique
- des fonctionnalités équivalentes aux applications additionnelles Graph 90+E préinstallées Physium, Graphe 3D, Sim Prob et Géométrie
Sur ce dernier point, si
Casio parle d'une mise à jour, cela pourrait signifier que ces fonctionnalités prendront cette fois-ci la forme d'applications intégrées au système d'exploitation, et qui donc à la différence resteraient utilisables en mode examen. Une belle évolution !
Restent donc à ce jour incertain l'avenir des :
- applications intégrées Programme, Lien, eActivity, E-CON4 et Finance
- application additionnelle Plot Image
Pour certaines de ces applications, on peut très facilement imaginer une suppression volontaire et donc définitive :
- eActivity qui peut être vu comme un éditeur d'anti-sèches (bien que permettant bien mieux que cela) et rencontrer donc une certaine hostilité de la part d'enseignants ou institutions, notamment lorsqu'il n'y a pas de mise en place systématique du mode examen (évaluations en classe, examens internationaux, autres pays vu que la Graph Math+ semble comme nous avons vu ne pas avoir été développée spécifiquement pour la France, etc.)
- l'application Programme puisque le langage Casio Basic n'est plus utilisé au lycée français - peut-être sera-t-elle à la différence toujours présente dans le système d'exploitation équipant les successeurs des fx-CG50
Casio te propose donc avec la
Graph Math+ une calculatrice qui évoluera avec tes besoins. Si tu la choisis en cette rentrée 2024 pour la Seconde ou la Première, tu pourras la mettre à jour gratuitement au premier semestre 2025 avec plein de fonctionnalités scientifiques, soit à temps pour une rentrée en Première ou Terminale, et peut-être même juste à temps pour le Baccalauréat 2025 si la mise à jour sortait suffisamment tôt dans l'année.
B) Application Calcul et menus transversauxGo to top 
L'application
Calcul s'organise en 3 onglets entre lesquels tu peux librement et surtout rapidement basculer à l'aide des 2 touches fléchées horizontales additionnelles que nous t'avons présentées :
- Calcul (affiché par défaut)
- Vecteur
- Matrice
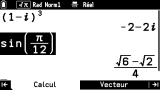
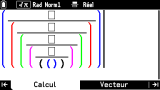
L'onglet
Calcul de l'application
Calcul est comme tu peux le deviner dédié à la réalisation de tes calculs.
Il te permet une saisie en écriture naturelle. On apprécie entre autres la double indication des paires de parenthèses correspondantes, aussi bien avec une taille adaptée à leur contenu qu'avec des couleurs
(jusqu'à 5 couleurs différentes).
Différents types de calculs et donc résultats y sont gérés :
- calcul numérique
- calcul complexe / imaginaire
- calcul vectoriel
- calcul matriciel
- calculs sur des listes que nous évoquerons plus loin
- calcul exact QPiRac pour les éléments réels des types précédents rentrant dans les 2 familles de nombres suivantes :
Les 30 derniers calculs ainsi que leurs résultats associés sont conservés et peuvent être remontés dans l'historique des calculs.
Il t'est par exemple possible de remonter l'historique avec la flèche vers le haut, de demander la modification d'une saisie avec l'une des flèches horizontales, puis de la réévaluer en place avec la touche
EXE
.
Belle amélioration, si à la différence tu remontes l'historique pour sélectionner un résultat au lieu d'une saisie, et revalides ce dernier avec la touche
EXE
, alors le résultat est copié et collé à la position du curseur dans la ligne de saisie en fin d'historique !
C'était quelque chose qui fonctionnait déjà sur
Graph 35+E II, mais pas sur
Graph 90+E.
Mais profitons du cadre offert par cet onglet
Calculs afin de te présenter les différents menus transversaux de la calculatrice.
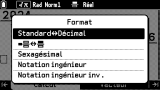
Le format du dernier résultat réel
(ou des composantes réelles du dernier résultat) peut être changé facilement d'un simple appui sur la touche
FORMAT
. Un menu
popup te propose alors systématiqument l'ensemble des choix suivants :
- écriture exacte QPiRac (Standard) ou bien décimale
- dans le cas d'une écriture exacte concernant un nombre rationnel, choix entre la notation sous forme de fraction ou bien de nombre mixte (écriture anglosaxonne spécifique aux fractions impropres, c'est-à-dire de valeur supérieure à 1)
- notation sexagésimale (décomposition de la partie décimale selon la base 60, utile pour les mesures d'angle en degrés ou encore de temps et durée)
- notation ingénieur (plus petite mantisse supérieure ou égale à 1 permettant l'utilisation d'une puissance de 10 avec un exposant multiple de 3)
- notation ingénieur inv (plus grande mantisse inférieure à 1 permettant l'utilisation d'une puissance de 10 avec un exposant multiple de 3)

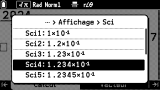
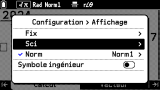
Comme tu peux voir, la notation scientifique usuelle au lycée français n'est hélas pas proposée via ce menu. Pour obtenir la notation scientifique tu dois aller changer le format d'affichage dans le menu
SETTINGS
. Des notations scientifiques avec de 1 à 10 chiffres significatifs te sont alors proposées. Mais ici à la différence ça ne basculera pas juste l'affichage du dernier résultat, mais celui de tous les résultats obtenus à partir de maintenant, jusqu'à un nouveau changement de ce réglage.
De façon similaire le menu
FORMAT
ne propose rien de spécifique lorsque le dernier résultat est un nombre complexe. Il te faudra ici encore aller dans le menu
SETTINGS
pour changer la forme de tous les résultats complexes. T'y sont proposés la forme algébrique, ainsi que la forme polaire qui n'est pas enseignée au lycée français. Elle est toutefois assez proche de la forme exponentielle qui pour sa part est gérée dans les saisies.
Le menu
FORMAT
est une idée remarquable, mais nous regrettons que son concept n'ait apparemment pas été poussé jusqu'au bout, l'obtention ponctuelle de certaines formes pourtant très usuelles au lycée demandant apparemment un changement de réglage, changement qu'il faudra par la suite défaire. Espérons que la mise à jour de 2025 ait prévu d'aller plus loin.
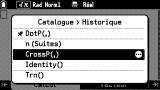

Pour toutes les opérations ou fonctions non disponibles au clavier, tu peux faire appel au menu
CATALOG
dont nous allons te présenter ici le fonctionnement général.
Ce menu transversal
(c'est-à-dire accessible depuis l'ensemble des applications adoptant la nouvelle interface, à l'exception de l'application Python disposant d'un catalogue spécifique) énumère pour tes saisies l'ensemble des fonctions ou opérations intégrées à la calculatrice.
Les fonctions sont ici accessibles sous plusieurs entrées au catalogue.
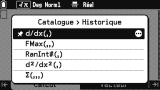
Innovation de la
Graph Math+, l'entrée
Historique conserve en mémoire tes 10 derniers choix validés dans le catalogue.
De plus, comme suggéré visuellement sur la sélection, la touche
...
te permet également d'épingler un ou plusieurs des choix mémorisés pouvant correspondre donc à des fonctions dont tu as souvent besoin. À la différence des autres, les choix épinglés sont protégés et ne seront pas écrasés lors de tes prochaines validations au catalogue. 👍
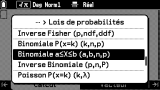
Les entrées suivantes te permettent de retrouver l'ensemble des fonctions regroupées dans différentes catégories. Citons entre autres :
- Étude de fonction : dérivées, intégrale, maximum et minimum locaux d'une fonction, opérateur de sommation (Σ), logarithmes, solveur, division euclidienne, simplification
- Probabilités : factorielle, fonctions de dénombrement, fonctions aléatoires
- Calcul numérique : pgcd, ppcm, valeur absolue, parties entière et fractionnaire, arrondis, reste division euclidienne
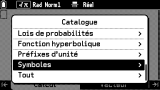
L'entrée
Symboles est dédiée à l'ensemble des opérateurs non alphabétiques.
Enfin l'entrée
Tout permet également d'accéder à l'ensemble des fonctions intégrées de façon alphabétique ; tu choisis d'abord la première lettre pour te voir alors présenter les fonctions associées par ordre alphabétique.
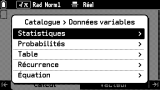
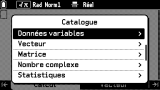
L'entrée
Données variables pour sa part permet d'accéder accès aux variables système, c'est-à-dire des variables préexistantes n'ayant pas été créées par l'utilisateur, destinées à accueillir les configurations ou résultats de certaines applications.
Perte de fonctionnalités toutefois, la
Graph 90+E te permettait d'accéder sur ton smartphone ou ta tablette à une aide en ligne concernant l'entrée sélectionnée au catalogue, via l'affichage d'un QR Code.
Le QR Code affiché par la calculatrice te conduisait en fait à la page du manuel en ligne traitant de l'entrée en question.
Nous n'arrivons pas à retrouver cette fonctionnalité sur
Graph Math+.
Sur certaines fonctions au catalogue,
Casio a fait l'effort sur
Graph Math+ d'indiquer les arguments attendus sur la même ligne au catalogue.
Mais malheureusement, c'est loin d'être le cas pour toutes les fonctions du catalogue et il n'est pas toujours évident de deviner ce qui est attendu comme arguments et surtout dans quel ordre...
Autre retrait par rapport à la
Graph 90+E, il n'est plus possible d'aller directement à une entrée du catalogue en saisissant ses premières lettres.
Tu n'as droit ici comme exposé plus haut qu'à la sélection de la 1
ère lettre via l'entrée
Tout, et au-delà tu dois prendre l'habitude de naviguer rapidement en exploitant les nouvelles touches fléchées de défilement d'écran vers le haut et vers le bas.
B4) Conversion d'unités et suffixes SIGo to top 
Attardons nous sur quelques délicieuses fonctionnalités scientifiques présentes au menu
CATALOG
.
L'entrée
Conversion d'unités permet de convertir une unité dans une autre unité de même type, une superbe fonctionnalité pour les Mathématiques et surtout les sciences expérimentales
(Physique-Chimie).
On distingue pour chaque type de conversion possible :
- 18 unités de longueur
- 9 unités d'aire
- 15 unités de volume
- 4 unités de température
- 5 unités de vitesse
- 10 unités de masse
- 5 unités de force
- 10 unités de pression
- 14 unités d'énergie
- 5 unités de puissance

Pour réaliser une conversion il te suffit de saisir dans l'ordre :
- la valeur à convertir
- son unité initiale
- l'opérateur de conversion (►) présent au même menu
- l'unité vers laquelle convertir
Précisons que tu n'as droit ici qu'aux unités présentes au menu. Les unités non listées ne peuvent pas être obtenues par composition d'unités existantes, et c'est bien dommage.
Exemple, pour les vitesses il n'y a pas l'unité
cm/s. Bien que l'unité
cm soit présente pour les longueurs et l'unité
s également pour le temps, la calculatrice ne comprend pas que ce que l'on veut dire si on a l'idée de saisir un quotient de ces deux unités...
C'est bien dommage cette restriction, les unités présentes au menu étant certes usuelles mais très loin d'être exhaustives. Il suffit donc d'un tout petit préfixe SI différent pour que l'unité dont on a besoin ne soit pas au menu, et nécessite une étape supplémentaire pouvant être génératrice d'erreurs.
Et bien justement, parlons de préfixes SI, car ils sont également au catalogue sous l'entrée
Préfixes d'unité.
11 préfixes allant de
femto (10-15) à
Exa 1018 sont gérés :
Mais malgré le titre de leur menu, ces préfixes ne semblent pas utilisables ici non plus pour constituer de nouvelles unités non présentes au menu, comme par exemple l'unité de longueur
pm.
Ils ont toutefois le mérite de simplifier l'étape supplémentaire nécessaire lorsque le menu précédent n'offrira pas l'unité souhaité avec le bon préfixe ; il faudra simplement effectuer une conversion de préfixe après la conversion d'unité.
Attention, l'opérateur de conversion précédent semble de plus ne pas fonctionner avec les préfixes. Astuce, pour convertir dans le préfixe souhaité, il te faudra effectuer une diviser par ce dernier.
On apprécie certes que ces fonctionnalités scientifiques essentielles au lycée et absentes de nombre de modèles graphiques d'entrée de gamme soient présentes.
Toutefois on retrouve très exactement les mêmes défauts que sur le modèle précédent Graph 90+E. Elles auraient pourtant bien eu besoin de quelque amélioration...
Mais ce sera peut-être pour la mise à jour majeure de 2025 qui justement va couvrir en grande partie les fonctionnalités de sciences expérimentales ?...
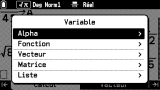
Autre menu transversal, celui appelé par la touche
VARIABLE
. Il te liste ici l'ensemble des variables définies par l'utilisateur ! 👍
Les noms de variables qu'il permet de saisir te sont accessibles par types :
- Alpha pour les 28 variables alphabétiques (26 lettres A à Z, auxquelles on ajoute r et θ)
- Fonction
- Vecteur
- Matrice
- Liste
Les variables listées sont de plus judicieusement accompagnées de leurs valeurs, même si nous regrettons que ce soit obligatoirement en écriture décimale, sans aucune possibilité de valeur exacte
QPiRac.
Peu importe donc qu'il s'agisse de nombres, fonctions, vecteurs, matrices ou listes, toutes ces variables définies par l'utilisation sont ici d'une simple touche immédiatement accessibles de façon transversale depuis l'ensemble des applications de la calculatrice, peu importe l'application à partir de laquelle la variable a été définie. De quoi progresser dans la résolution d'un problème sous diverses représentations !
Seule exception, l'application
Python qui dispose d'un menu spécifique avec les seules variables affectées en langage
Python.
B6) Onglet Vecteur et calcul vectorielGo to top 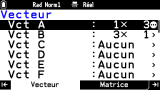
Nous avons donc ici un onglet
Vecteur en permanence sous la main, afin de définir les vecteurs pouvant être utilisés dans l'onglet
Calcul. Plus besoin d'aller chercher dans des sous-menus onglets comme sur
Graph 90+E !
26 vecteurs nommés de
Vct A à
Vct Z peuvent être affectés ou consultés directement dans cet onglet, auxquels s'ajoute le vecteur
Vct Ans associé au dernier résultat vectoriel.
La dimension de chaque vecteur peut aller jusqu'à
999.
Une fois les dimensions précisées, dans cet onglet les différentes coordonnées d'un vecteur sont affichées sous la forme d'un tableau en écriture décimale, et se saisissent en écriture ligne. Il est possible de rappeler en écriture ligne la valeur exacte de la coordonnée sélectionnée, mais les valeurs exactes en question seront limitées aux seuls nombres rationnels.
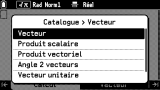
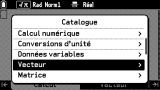
Une fois revenu sur l'onglet
Calcul, les fonctions de calcul vectoriel peuvent être saisies via le menu
CATALOG
sous l'entrée
Vecteur. Y sont disponibles entre autres les produits scalaire et vectoriel.
Les noms de vecteurs quant à eux peuvent être saisis via le menu
VARIABLE
sous l'entrée
Vecteur également. Même si c'est en écriture décimale, le menu en question a la bonne idée d'indiquer les valeurs des vecteurs en question !
Et chose remarquable, ici les différentes coordonnées sont bien affichées en écriture exacte
QPiRac le cas échéant, et même les coordonnées complexes sont gérées !
B7) Onglet Matrice et calcul matricielGo to top 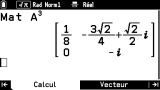
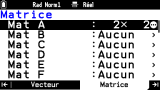
De façon similaire, nous avons également sous la main un onglet
Matrice afin de définir les matrices pouvant être utilisées dans l'onglet
Calcul.
Ici aussi
26 matrices nommées de
Mat A à
Mat Z peuvent être affectées ou consultées dans cet onglet, auxquelles s'ajoute la matrice
Mat Ans associée au dernier résultat matriciel.
Chaque matrice peut avoir jusqu'à
999 lignes ou
999 colonnes. En pratique toutefois, le nombre maximum d'éléments est contrairement par la mémoire et se chiffre autour de 5000.
Là encore une fois les dimensions précisées, les différents éléments des matrices se saisissent en écriture ligne à partir d'un tableau et s'y affichent en écriture décimale. L'élément sélectionné est rappelé en bas d'écran en écriture ligne, mais avec des valeurs exactes limitées aux seuls nombres rationnels.
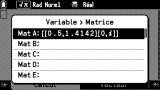
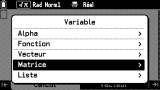
Une fois revenu sur l'onglet
Calcul, les noms de matrices à utiliser pour les calculs sont à saisir via le menu
VARIABLE
sous l'entrée
Matrice. On apprécie ici aussi dans ce menu le rappel des valeurs de matrices en écriture ligne décimale.
Ici encore les fonctions de calcul matriciel non présentes au clavier doivent être saisies via le menu
CATALOG
sous l'entrée
Matrice.
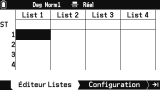

Passons à l'application
Stats. Ici c'est différent, l'application comporte de 3 à 5 onglets :
- Editeur Listes (affiché par défaut)
- Configuration
- et en fonction du type de tâche sélectionnée sur ce dernier onglet :
- Graphe
- Résultat
- Graphe régress

L'onglet
Editeur Listes permet de définir des listes de valeurs.
26 listes sont gérées, nommées de
List 1 à
List 26, permettant aussi bien la saisie d'une série de données statistiques sur laquelle on va travailler dans cette application, que les calculs sur des listes dans l'application
Calcul. S'ajoute dans ce dernier cas la liste
List Ans pour le dernier résultat ayant pris la forme d'une liste.
Chaque liste peut contenir jusqu'à
999 éléments.
Chacune de ces listes peut de plus être nommée sur 8 caractères alphanumériques via la ligne
ST, et ensuite appelée directement par ce nom
(List "NOM") dans les saisies de calculs si tu préfères.
Tu as besoin de travailler sur des données conséquentes ?
Casio a également prévu cela. Le menu contextuel
...
te permet d'importer les données à partir d'un fichier
.csv (le séparateur de valeur étant si besoin configurable dans l'application Paramètres) !
Inversement, il t'est possible d'exporter les données au format
.csv pour poursuivre leur traitement sur ordinateur !
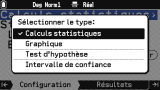
Passons à l'onglet
Configuration, c'est ici que tout se joue.
La calculatrice permet de choisir la tâche que tu souhaites accomplir sur la série statistique saisie :
- Calcul statistiques
- Graphique
- Test d'hypothèse
- Intervalle de confiance
La tâche choisie est alors à configurer.
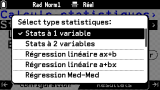
Pour la tâche
Calcul statistiques, tu peux configurer plusieurs sous-tâches au choix:
- Stats à 1 variable
- Stats à 2 variables
- et 12 choix de formes de Régression
Dans le cas de calculs statistiques à 1 ou 2 variables, l'onglet
Configuration te demande de préciser les listes correspondant aux valeurs des variables. Concernant les effectifs de ces valeurs, tu peux soit les mettre à 1, soit spécifier une autre liste.
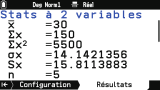
Tu as ensuite accès sur l'onglet suivant
Résulats aux paramètres de la série statistique.
Nombre de paramètres sont gérés pour chaque variable :
- paramètres de position :
- moyenne
- minimum et maximum
- 1er et 3e quartile (respectant par défaut la définition non internationale utilisée au lycée Français)
- médiane
- mode
- paramètres de dispersion :
- écart-type (population ou échantillon)
- effectifs et fréquences :
- effectif total
- effectif ou fréquence du mode
- paramètres sommatifs :
- somme des valeurs
- somme des carrés
- somme des produits (si 2 variables)
Et précisons que les quartiles respectent par défaut la définition non internationale utilisée au lycée Français !
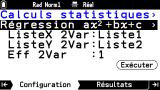
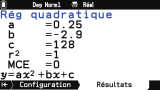
Dans le cas d'une série statistique à 2 variables
(au moins 2 listes/colonnes de valeurs remplies), il t'est aussi possible d'effectuer une régression.
Nombre de modèles de régressions sont ici gérés, et tu obtiendras ici encore dans l'onglet
Résultats les paramètres optimaux de l'équation choisie :
- linéaire
$mathjax$y=ax+b$mathjax$
ou $mathjax$y=a+bx$mathjax$
- droite Med-Med
$mathjax$y=ax+b$mathjax$
- quadratique
$mathjax$y=ax^2+bx+c$mathjax$
- cubique
$mathjax$y=ax^3+bx^2+cx+d$mathjax$
- quartique
$mathjax$y=ax^4+bx^3+cx^2+dx+e$mathjax$
- logarithmique
$mathjax$y=a+b\dot ln(x)$mathjax$
- exponentielle
$mathjax$y=a\dot e^{bx}$mathjax$
- exposant
$mathjax$y=a\dot b^x$mathjax$
- puissance
$mathjax$y=a\dot x^b$mathjax$
- sinusoïdale
$mathjax$y=a\dot sin(bx+c)+d$mathjax$
- logistique
$mathjax$y=\frac{c}{1+a\dot e^{-bx}}$mathjax$
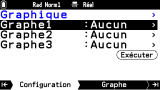
Remontons, la tâche
Graphique te permet de représenter ta série statistique sous la forme d'un ou plusieurs diagrammes.
Divers types de diagrammes sont configurables, et leur tracé sera obtenu et visualisable sur l'onglet
Graphe :
- nuage de points
- graphique linéaire xy
- diagramme en boîtes (ou à moustaches), avec même la détection de valeurs aberrantes
- histogramme
- diagramme en ligne brisée
- diagramme circulaire
- diagramme en barres
- tracé probabilité normale
- courbe de densité normale
- et 11 des choix de régressions précédents (à l'exception de Med-Med)
Tu peux définir et superposer jusqu'à 3 diagrammes pour ta série :
Dans le cas particulier de choix de représentations en nuages de points, lignes brisées ou courbes, t'est rajouté un dernier onglet
Graphe régress.
A priori il représente exactement la même chose que l'onglet
Graphe, mais c'est ici le menu contextuel
...
qui change, te permettant de superposer un graphe de régression à ton diagramme.


Il t'est même possible de superposer plusieurs graphes de régression via le menu contextuel de la touche
...
!
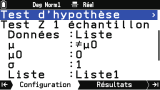
Autre tâche possible,
Test d'hypothèse :
- Tests Z à 1-2 échantillons ou 1-2 proportions
- Tests t à 1-2 échantillons ou de régression linéaire
- Tests χ² d'adéquation ou à 2 voies
- Test F à 2 échantillons
- Analyse de variance
Sont alors présents les onglets :
- Résultats pour les résultats du test
- Graphe pour une interprétation graphique
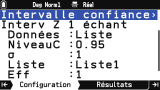
Et enfin dernière tâche possible, l'
Intervalle de confiance :
- Intervalle Z à 1-2 échantillons ou 1-2 proportions
- Intervalle t à 1-2 échantillons
L'intervalle déterminé pour la configuration précisée sera retourné et consultable dans l'onglet
Résultats.

Petit passage par l'application
Probabilités, dédiée aux questions de lois de probabilités. L'application présente ici 3 onglets te distinguant très clairement les différentes étapes à suivre dans la résolution de tes problèmes :
- Sélectionner (affichée par défaut)
- Configuration
- Résultats
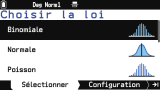
L'onglet
Sélectionner, permet ici de préciser la loi de probabilités à utiliser.
Tu disposes de pas moins de 8 lois de probabilités au choix :
- 4 lois discrètes : binomiale, Poisson, géométrique, hypergéométrique
- 4 lois continues : Normale, χ², Student, Fisher
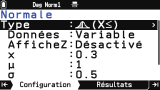
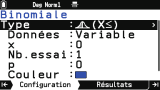
L'onglet
Configuration permet quant à lui de préciser les paramètres de la loi de probabilités choisie.
Enfin, nous arrivons sur la page
Résultats et c'est un véritable régal.
Déjà, pour limiter tout risque d'erreur,
Casio a pris le soin d'inclure sur cette page une ligne de rappel des paramètres de la loi saisis sur la page
Configuration.
Au-delà de cela, l'interface utilisateur de la page
Résultats est en effet d'une intuitivité absolument remarquable, parlant littéralement le langage scolaire de l'utilisateur.
Tout se passe en effet autour d'une relation de probabilités. Il y a juste à saisir sélectionner un des paramètres de la relation et y saisir la valeur connue de l'énoncé, afin que la calculatrice résolve automatiquement le ou les autres paramètres et mette à jour la relation avec leur(s) valeur(s) ! 👍
La forme de la relation de probabilités autour de laquelle on travaille est de plus au choix, ce qui permet de couvrir un très large éventail de questions types :
- P(X=…)=… (lois discrètes uniquement - la saisie n'est autorisée que pour le premier paramètre)
- P(X≤…)=…
- P(X≥…)=…
- P(…≤X≤…)=… (le saisie du dernier paramètre n'est autorisée que pour une loi Normale)
Pour une meilleure compréhension, nous avons même une interprétation graphique directement intégrée à la page
Résultats et mise à jour immédiatement à chaque modification !
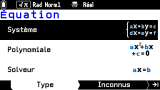

Dans l'application
Equations, un premier onglet
Type affiché par défaut te permet de choisir le type d'équations que tu souhaites résoudre :
- Système
- Polynomiale
- Solveur
Notons que ces choix sont tous très clairement illustrés par l'affichage en écriture naturelle de formes d'équations, différenciant de plus inconnues et paramètres via des couleurs !
En fonction du choix te seront épinglés différents onglets, distinguant clairement autants d'étapes à suivre pour parvenir aux solutions.

Le choix
Système te permet de résoudre des systèmes d'équations linéaires.
Les onglets à parcourir dans l'ordre sont ici :
- Inconnus pour choisir le nombre d'inconnus et donc d'équations, jusqu'à 6 au maximum
- Editeur pour saisir les coefficients des équations ainsi configurées, en écriture ligne, et même les coefficients complexes sont gérés !
Sur cet onglet, le coefficient sélectionné voit sa valeur rappelée en bas à droite, mais uniquement en écriture ligne avec des valeurs exactes limitées à Q. - Résultats pour obtenir la ou les solutions, avec gestion des cas avec infinité de solutions ou aucune solution.
Chaque valeur sélectionnée est rappelée en bas à droite, mais ici en écriture naturelle exacte QPiRac !
Un outil extrêmement puissant qui pourra t'accompagner au-delà du lycée ! 👍
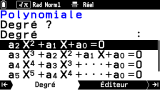
Le choix
Polynomiale te permet de trouver les racines de polynômes.
Les onglets épinglés t'indiquant les étapes à suivre sont alors ici :
- Degrés pour choisir le degré du polynôme, jusqu'à 6, avec à chaque fois pour plus de clarté la forme de l'équation impliquée !
- Editeur pour saisir les coefficients du polynôme ainsi configuré, toujours en écriture ligne.
Sur cet onglet, le coefficient sélectionné voit sa valeur rappelée en bas à droite, mais de nouveau uniquement en écriture ligne avec des valeurs exactes limitées à Q. Les coefficients complexes ne sont pour leur part pas acceptés ici. - Résultats pour obtenir les racines.
Chaque valeur sélectionnée est rappelée en bas à droite, mais de nouveau dans ce cadre cet onglet offre l'écriture naturelle exacte QPiRac !
Enfin, le choix
Equation te permet de résoudre une équation saisie librement sous la forme de ton choix. L'équation peut même faire appel à plusieurs paramètres dont tu pourras alors préciser les valeurs avant de la résoudre pour l'inconnue choisie.
C4) Application Graphe&Table et zone graphiqueGo to top 
L'application
Graphe&Table présente 3 onglets :
- Fonction (affiché par défaut)
- Graphe
- Table
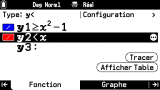
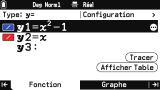
L'onglet
Fonction permet de définir la ou les fonctions avec lesquelles on souhaite travailler, jusqu'à
20 fonctions simultanément.
Pour chacune, l'application gère nombre de types de relations. Le type de la ou des prochaines relations à saisir peut à tout moment être être modifié via le menu ouvert par la ligne
Configuration :
- fonctions cartésiennes y=f(x)
- fonctions polaires r=f(θ)
- fonctions paramétriques
- fonctions x=f(y) (dont fonctions réciproques)
- inéquations (y≤f(x), x>f(y), ...)
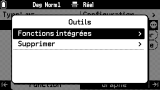
Sur une ligne de définition de fonction, le menu contextuel te facilite entre autres la saisie en te donnant accès à une liste de formes usuelles :
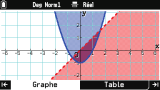
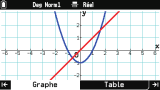
Mais si maintenant on tente depuis l'onglet
Fonction de passer à l'onglet
Graphe, on se rend compte que
Casio a fait quelque chose de très spécial. En effet l'on n'obtient pas de suite la représentation graphique attendue ; à la place l'utilisateur se voit obligatoirement présenter une fenêtre
popup de configuration de la fenêtre graphique.
Rien de méchant, la configuration en question est préremplie
(et si besoin plusieurs configurations prédéfinies sont accessibles). Cette popup de configuration est donc simplement montrée à l'utilisateur lorsqu'il tente d'accéder à la représentation graphique ; il peut très bien ne rien y changer et l'appliquer immédiatement grâce au bouton d'action
Tracer justement présenté en toute première ligne. Mais c'est ici encore une nouveauté d'une pertinence remarquable, rien que de voir cette configuration pendant un court instant donnant ainsi davantage de sens dans l'esprit de l'utilisateur à la représentation graphique qui va suivre ! 👍
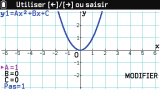
Belle surprise, il semble y avoir un support des fonctions paramétrées, c'est-à-dire les fonctions dont la définition fait appel à un ou plusieurs paramètres, variables autres que la variable de la fonction.
Avec la représentation de la fonction paramétrée sélectionnée, il suffit de faire appel au menu contextuel
...
où l'on trouve alors l'entrée
Modifier. Les différents paramètres sont alors automatiquement détectés, et on peut observer l'effet qu'a sur la représentation graphique leur modification selon différents pas. À chaque fois pour mieux comparer, nous avons non seulement l'affichage du graphe modifié mais également de l'ancien graphe ! Il s'agit donc d'un remplacement ici intégré aux fonctionnalités qu'offrait l'application distincte
G-dynamique sur
Graph 90+E !
Vu que
Casio annonce malgré tout des fonctionnalités
G-dynamique pour la mise à jour de 2025, il pourrait s'agir à la différence des animations qui ne semblent pas présentes ici.
Nous notons au passage l'utilisation déjà évoquée et fort bienvenue de messages d'aide en ligne dans la barre d'état en haut d'écran.
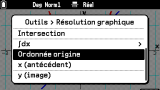
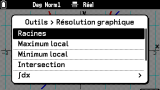
On retrouve bien évidemment tous les outils pertinents pour travailler sur les représentations graphiques : suivi de courbe, images et antécédents
(avec même les traits de constructions), zéros, ordonnée à l'origine, points d'intersections, tangente en un point, nombre dérivé, intégrale, aire entre deux courbes, etc.
Puisque nous avons nos premiers graphes, parlons un petit peu zone graphique. C'est la zone rectangulaire de l'écran utilisée pour l'affichage du repère des fenêtres graphiques. Ses pixels intérieurs sont librement allumables pour le tracé des graphes de fonctions, mais également diagrammes statistiques, représentations graphiques de suite... ou encore instructions graphiques de programmes en langage
Casio Basic qui n'existe plus ici.
Pour la déterminer, il suffit d'effectuer un petit calcul avec les bornes de la fenêtre graphique :
Sauf qu'ici sur
Graph Math+, nous ne trouvons apparemment plus de variable système permettant d'accéder à la configuration de la fenêtre graphique… Nous avons notamment cherché au menu
CATALOG
sous l'entrée
Données variables, sans succès. Très étrange de ne plus pouvoir accéder directement à ces valeurs et donc en tenir compte dans un calcul.
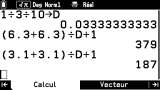
Alternative, consultons la configuration de la fenêtre graphique et recopions les valeurs pour le calcul. Comme la configuration en question donne certes
Δx, écart horizontal selon l'échelle entre 2 pixels adjacents
(sous le nom Valeur point x) mais pas
Δy, nous opterons de plus pour un repère orthonormé impliquant
Δx=Δy.
Pareil donc que sur
Graph 90+E, nous trouvons toujours très exactement une zone graphique de
379×187 pixels, dans le contexte de l'ensemble des applications offrant une représentation graphique dans un repère.
Plus précisément, il s'agit des dimensions de la zone graphique visible lorsque l'on masque la barre d'onglets à l'aide de la touche
AC
ou encore si plus accessible de la touche fléchée de défilement d'un écran vers le bas.
- 320×240=76800 pixels : HP Prime
- 379×187=70873 pixels : Casio Graph 90+E, Graph Math+
- 318×212=67416 pixels : TI-Nspire CX II
- 320×204=65280 pixels : NumWorks
- 265×165=43725 pixels : TI-82 Advanced Edition Python, TI-83 Premium CE Edition Python
- 127×63=8001 pixels : Casio Graph 35+E II
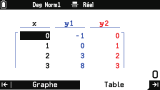
Enfin, l'onglet
Table permet d'obtenir un tableau de valeurs d'une ou plusieurs fonctions.
Superbe innovation ici aussi, le menu contextuel de la touche
...
te permet d'accompagner le tableur de valeurs d'une représentation graphique en nuage de points, et même d'y mettre en évidence la valeur sélectionnée ! 👍

L'application
Suite te permet de travailler avec des suites numériques.
Elle dispose de 2 onglets :
- Suite (affiché par défaut)
- Table
Sur Graph 90+E les définitions de suites étaient pénibles.
En effet, rang initial et dans le cas de suites récurrentes terme initial, étaient à définir et consulter sur un écran distinct de celui de saisie de la définition par le terme général ou bien de la relation de récurrence.
C'était générateur de nombre d'erreurs chez les élèves....
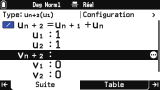
L'onglet
Suite te permet de définir jusqu'à
3 suites simultanément.
Pour chacune plusieurs formes de définitions te sont proposées au choix :
- terme général
- récurrence d'ordre 1
- récurrence d'ordre 2
Et donc une très belle évolution dans le cadre de suites définies par récurrence, est qu'ici tous les éléments de la définition sont présents sur un seul et unique écran ! 👍

L'onglet
Table affiche alors par défaut le tableau de valeurs associé.
La représentation graphique associée est également accessible sur ce même onglet via la touche menu contextuel
...
, soit à la place du tableau soit en plus.
Dans le cas de suites définies par récurrence, il est possible d'opter à la place du nuage de points pour une représentaiton dite en toile d'araignée et même d'animer son tracé étape par étape :

Passons maintenant à l'application
Python afin de voir si
Casio nous a ici aussi inventé quelque chose de génial.
L'application présente 2 onglets :
Jusqu'à présent, les applications Python des calculatrices faisaient quasiment toutes démarrer l'utilisateur dans la liste des scripts, parfois même pire dans un explorateur de fichiers (exception avec la HP Prime qui s'ouvrait directement dans la console Python). Ce cas mis à part, l'utilisateur devait donc de façon quasi systématique faire la manipulation permettant de créer un script ou pire fichier après avoir navigué vers le bon dossier, et d'en saisir le nom au clavier alphabétique. C'était entre autres le cas pour la Graph 90+E.
Qu'est-ce que c'était lourd, long et compliqué... Rajoutons que nous sommes hélas de plus en plus sur des générations d'utilisateurs qui ont de plus en plus de mal à comprendre et distinguer fichiers et dossiers, les appareils numériques qu'ils utilisent ayant tendance à leur masquer cet aspect informatique, et ne parlons même pas de dossier racine ou encore dossiers compressés (archives).

Et bien l'application
Python s'ouvre ici sur l'onglet
Editeur, et c'est déjà quelque chose d'absolument remarquable.
En effet justement, quand on fait du
Python en classe, le but est le plus souvent de saisir et tester un petit script
(et non de réutiliser un script déjà existant), dans la plupart des cas sans volonté de le conserver. On réutilise et conserve plutôt nos scripts dans le cadre de projets, un cas d'utilisation moins fréquent à la fois en fréquence dans le temps et ainsi qu'en effectif car concernant moins d'utilisateurs.
Casio ose donc changer tout ça. Avec la
Graph Math+, le lancement de l'application
Python présente directement la page de l'éditeur de script. Ce dernier est préconfiguré avec un script déjà prénommé
module.py, et donc immédiatement prêt à être exécuté sans manipulation supplémentaire à faire après ou avant la saisie du code ! Que de manipulations économisées et que de temps de gagné !👍
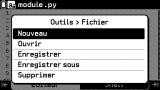
Rassure-toi, l'utilisateur conserve bien évidemment la possibilité de sauvegarder son script après saisie si il le souhaite, sous le nom de son choix, grâce au menu contextuel de la touche
...
.
Si à la différence tu n'as définitivement plus rien à faire du contenu de
module.py et souhaites repartir sur un tout nouveau script, pas davantage besoin ici de manipulations de fichiers, il te suffit juste de taper
AC
pour vider le contenu de l'éditeur !
Attention une fois arrivé sur la liste des scripts.
D'une part, si tu rajoutes
(via un ordinateur par exemple) des scripts dont le nom hors extension occupe plus de 8 caractères, l'affichage de leur nom sera tronqué sur 6 caractères ou moins, afin de laisser la place à un suffixe de numérotation
('~1', '~2', etc.), en fonction du nombre de fichiers partageant la même troncature.
C'est caractéristique de l'utilisation d'un système de fichiers
FAT, mais avec ici le système d'exploitation qui ne gèrerait apparemment pas correctement les noms de fichiers longs
(plus de 8 caractères hors extension de fichier).
D'autre part, contrairement à la
Graph 90+E, les raccourcis alphabétiques ne marche plus à cet écran sur
Graph Math+. Il n'est plus possible d'aller dans la liste directement au premier script commençant par une lettre donnée,
Casio te force ainsi à t'habituer au nouveau pavé de navigation avec notamment ses flèches de défilement d'écran vers le haut et vers le bas.
L'éditeur
Python sur
Graph 90+E souffrait d'une lourde limitation. Comme évoqué plus haut, il utilisait la même police de caractères que toutes les autres interfaces de la calculatrice, c'est-à-dire une police de caractères énorme pour que ces interfaces aient toujours le même nombre de lignes et de colonnes que sur le petit écran de la
Graph 35+E II. Cela limitait son affichage à seulement
7 lignes sur
21 colonnes, fort inconfortable car ne permettant pas une bonne vue d'ensemble des scripts saisis.
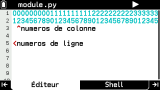
Et bien nous avons droit à une belle surprise, l'éditeur
Graph Math+ permettant de visualiser les scripts
Python sur :
- 9 lignes (on pourrait même dire 9,5 lignes) au lieu de 7
- 35 colonnes au lieu de 21
Une amélioration très significative ! 👍
Mais ce n'est pas tout, là où la
Graph 90+E affichait le seul numéro de la ligne sur laquelle était positionné le curseur de texte, sur
Graph Math+ nous avons droit à une numérotation complète des lignes dans la marche à gauche ! 😍
Comme sur
Graph 90+E, nous continuons à bénéficier de l'indentation automatique ainsi que de la coloration syntaxique.
Le parcours de scripts plus longs est fort aisé à l'aide des nouvelles touches de défilement d'écran vers le haut ou vers le bas, et le menu contextuel permet même d'aller directement à un numéro de ligne spécifié, par exemple pour aller corriger suite à un message d'erreur au lancement.

Ce n'était toutefois pas la seule limitation de l'éditeur
Python sur
Graph 90+E. L'éditeur refusait malgré tout d'ouvrir :
- tout script dépassant 300 lignes
- tout script avec au moins une ligne dépassant les 255 caractères (caractère de retour à la ligne exclu)
Si tu conservais la possibilité de lancer ces scripts, il t'était impossible, sur calculatrice, de visualiser leur code et encore moins le modifier.
Malheureusement pas de changement ici, l'éditeur de la
Graph Math+ conserve cette limitation de 300 lignes et 255 caractères. Une fois la limite atteinte, la saisie selon le cas de toute ligne ou tout caractère supplémentaire te sera impossible. Et de même, importer depuis un ordinateur un script dépassant ces limitations donnera une erreur dans l'éditeur, même si il restera toujours possible de le lancer manuellement depuis la console
Python via la commande
import.
Attention également, tout comme sur
Graph 90+E, l'éditeur
Python ne semble supporter que les caractères ASCII 7 bits.
Si tu importes depuis un ordinateur un script comprenant des caractères dits spéciaux, comme les lettres accentuées, ils seront tous remplacées par des espaces.

Besoin de saisir un caractère non présent au clavier pour tes scripts ou appels
Python ?
Sur
Graph 90+E c'était possible en ouvrant la table des caractères, qui te permettait alors de choisir entre
94 caractères différents, correspondant tous à de l'ASCII 7 bits.
Un inconvénient était toutefois qula table s'ouvrait en plein écran et masquait donc durablement le contexte d'appel, alors que pouvant être utile pour être sûr de sa saisie.
Sur
Graph Math+, aussi bien depuis l'éditeur que la console
Python, le menu contextuel
...
te permet d'accéder à un outil de sélection de caractères.
Grosse évolution, il ne s'ouvre plus en plein écran mais se superpose à la barre d'onglets en bas d'écran.
Les flèches verticales te permettront de sélectionner entre 4 lignes de caractères, et les flèches horizontales sur chaque ligne le caractère à saisir.
On passe ici de
94 à
95 caractères sélectionnables via cet outil, le caractère supplémentaire étant tout simplement l'espace.
D3) Menu CATALOG et bibliothèques PythonGo to top 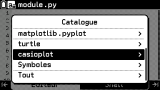
Contrairement à ce que beaucoup trop de personnes n'ayant pas essayé croient, la saisie de scripts
Python sur calculatrice ce n'est pas fastidieuse.
Chez
Casio, on bénéficie avantageusement du menu
CATALOG
qui est ici dédié au
Python, et permet une saisie rapide des noms de bibliothèques ou fonctions sans avoir à les taper lettre par lettre !
Le menu nous indique entre autres les bibliothèques disponibles, et nous permet d'accéder à tout ce qui concerne chacune d'entre elles :
- intégré pour la bibliothèque builtins
- bibliothèque math
- aléatoire pour la bibliothèque random
- bibliothèque matplotlib.pyplot pour les tracés dans un repère
- bibliothèque turtle pour les tracés par déplacement d'une tortue
- bibliothèque casioplot qui, sur Graph 90+E, permettait les tracés par pixels
Ici ce sont donc les seules bibliothèques décrites au menu, et il pourrait très bien y avoir d'autres bibliothèques intégrées qui fonctionneraient dans la console sans être indiquées au menu.
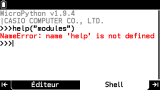
Si il est facile en
Python de demander la liste complète des bibliothèques intégrées avec un
help("modules"), malheureusement
Casio n'a pas inclus la fonction
help() dans son implémentation de la bibliothèque
builtins.
Nous avions creusé sur
Graph 90+E et n'avions trouvé rien d'autre que ce qu'il y avait au menu ; nous considérerons que c'est pareil ici, et qu'il s'agit donc de nouveau de l'implémentation
Python la plus timide toute concurrence confondue.
Si tu préfères accéder aux fonctions non pas par catégories mais de façon alphabétique, c'est ici encore disponible sous l'entrée
Tout, et tu y retouveras aussi bien ce qui concerne la bibliothèque
builtins que l'ensemble des autres bibliothèques !
Enfin, comme avec l'outil de sélection de caractères précédent tu peux ici accéder aux caractères non présents au clavier sous l'entrée
Symboles, et tu trouveras ici en prime de quoi saisir également en une seule fois les opérateurs utilisant plusieurs caractères :
D4) Onglet Shell et interpréteur PythonGo to top 
Passons enfin sur l'onglet
Shell en question.
C'est ici que nous avons donc accès à la console
Python, et le dernier script ouvert dans l'éditeur y est automatiquement importé.
Nous pouvons alors y saisir nos appels
Python et bénéficier de l'historique des derniers appels et sorties. Comme dans l'application
Calculs la flèche vers le haut permet ici de remonter dans l'historique ligne par ligne, et il suffira alors de valider la ligne sélectionner pour la copier-coller dans la ligne de saisie.
Comme indiqué en en-tête, l'interpréteur utilisé est ici
Micropython, une implémentation allégée de
Python 3.4 pour microcontrôleurs.
Plus précisément ici il s'agit, comme sur
Graph 90+E, de
Micropython 1.9.4, une version remontant à mai 2018.
Casio n'a donc visiblement pas profité de l'occasion pour rafraîchir son interpréteur
Micropython qui reste, à égalité avec la
HP Prime, le plus ancien interpréteur
Micropython sur les modèles actuels de calculatrices graphiques.
- MicroPython 1.17.0 : NumWorks
- MicroPython 1.11.0 : TI-Nspire CX II
- MicroPython 1.9.4 : Casio Graph 35+E II, Graph 90+E, Graph Math+
- CircuitPython : TI-82 Advanced Edition Python, TI-83 Premium CE Edition Python (dérivé allégé de MicroPython)
Les interpréteurs MicroPython ou similaires qui tournent sur calculatrices font appel à 2 types de mémoires essentielles lors de l'évaluation de tes appels Python.
L'une d'entre elles est le tas (heap) qui stocke, à l'exécution, le contenu des objets Python créés. Il limite donc la taille globale utilisée pour les données des différents objets Python créés.
Un appel très simple permet usuellement d'en déterminer la capacité en octets :
gc.mem_alloc() + gc.mem_free().
Sauf que, comme nous avons vu, la bibliothèque
gc n'est pas au menu catalogue, et n'est pas davantage disponible dans le
Shell.
Il nous faut donc trouver une autre méthode.
Donnons quelques éléments de taille en mémoire d'objets
Python usuels :
objets | plateformes 32 bits | plateformes 64 bits |
entier | 12 octets
+2 octets par groupe de 15 bits nécessaire pour coder l'entier | 24 octets
+4 octets par groupe de 30 bits nécessaire pour coder l'entier |
chaîne | 25 octets
+1 octet par caractère | 49 octets
+1 octet par caractère |
liste | 29 octets
+4 octets par élément
+ tailles de chaque élément | 56 octets
+8 octets par élément
+ tailles de chaque élément |
tuple | 20 octets
+4 octets par élément
+ tailles de chaque élément | 40 octets
+8 octets par élément
+ tailles de chaque élément |
Nos calculatrices étant au mieux des plateformes 32 bits, voici une fonction qui retourne la taille d'un objet selon ces règles :
- Code: Select all
def size(o):
t = type(o)
s = t == str and 25 + len(o)
if t == int:
s = 12
while o:
s += 2
o >>= 15
elif t == list:
s = 28 + 4*len(o)
for so in o:
s += size(so)
return s
Nous allons donc tenter plutôt de remplir le
heap avec plusieurs objets que nous allons faire grandir chacun son tour jusqu'à déclenchement d'une erreur, et retourner la capacité maximale que nous avons réussi à consommer. Voici donc une fonction en ce sens :
- Code: Select all
def mem(v=1):
try:
l=[]
try:
l.append(0)
l.append(0)
l.append("")
l[2] += "x"
l.append(0)
l.append(0)
while 1:
try:
l[2] += l[2][l[1]:]
except:
if l[1] < len(l[2]) - 1:
l[1] = len(l[2]) - 1
else:
raise(Exception)
except:
if v:
print("+", size(l))
try:
l[0] += size(l)
except:
pass
try:
l[3], l[4] = mem(v)
except:
pass
return l[0] + l[3], max(l[0], l[4])
except:
return 0, 0
Cette fonction va ainsi nous permettre d'estimer la capacité
heap.
Précisons que le fonctionnement de la fonction est très fortement dépendant de l'état mémoire, et comme nous n'avons pas la bibliothèque
gc il ne nous est pas possible de nettoyer la mémoire en appelant
gc.collect().
Afin de limiter ces écarts, nous appellerons la fonction immédiatement après avoir ouvert l'application
Python.

Que ce soit sur
Graph 90+E ou
Graph Math+, un appel
mem() arrive à nous trouver dans les
1,029 Mo de mémoire
heap utilisable, avec au mieux jusque dans les
393 Ko de données contiguës.
Il ne semble donc pas y avoir eu d'amélioration de la part de
Casio par ici, mais peut-être tout simplement parce que la capacité
RAM n'a pas varié, ce que nous regarderons dans un moment.
Malgré tout, cela reste une capacité extrêmement confortable par rapport à la concurrence de milieu de gamme
(on peut citer le très insuffisant 64,888 Ko sur NumWorks ou encore pire 19,968 Ko sur TI-82 Advanced Edition Python et TI-83 Premium CE Edition Python), rendant à la différence parfaitement envisageable le développement d'interfaces graphiques ou même jeux graphiques, du moins si la bibliothèque graphique nous fournit ce qu'il faut, ce que nous verrons dans un moment.
- 252,100 Mo : HP Prime G2
- 2,068 Mo : TI-Nspire CX II-T
- 1,029 Mo : Graph 90+E, Graph Math+
- 100,432 Ko : Graph 35+E II
- 64,888 Ko : NumWorks
- 19,968 Ko : TI-82 Advanced Edition Python, TI-83 Premium CE Edition Python
D6) Capacité de la pile mémoire (stack)Go to top La pile
(stack) est l'autre mémoire essentielle pour l'exécution des tes appels ou scripts
Python.
À la différence du
heap, la mémoire
stack ne stocke pas mais référence, à l'exécution, les objets
Python en cours d'utilisation
(noms, types, adresse des données), dont les appels de fonctions en cours. Sa capacité limite donc le nombre d'objets Python pouvant coexister simultanément en mémoire, dont entre autres le nombre d'appels récursifs.
Nous n'avons pas ici de méthode pour chiffrer la capacité du
stack, mais nous pouvons toutefois compter le nombre maximum d'appels récursifs jusqu'à déclenchement d'une erreur.
Voici un script en ce sens :
- Code: Select all
def compte_r(n):
return n>0 and 1 + compte_r(n-1)
def test(f):
n = 0
try:
while 1:
n = f(n) + 1
except Exception as e:
print(e)
return n
Ici encore, aussi bien sur
Graph 90+E que
Graph Math+, l'appel
test(compte_r) nous indique pouvoir réaliser
82 appels récursifs avant épuisement de la capacité du
stack.
Donc pas d'amélioration ici non plus, pour un résultat confortable dans la moyenne du milieu de gamme couleur
(seulement 28 sur TI-82 Advanced Edition Python et TI-83 Premium CE Edition Python, mais 128 sur NumWorks).
- 202 : TI-Nspire CX II-T
- 128 : NumWorks
- 82 : Graph 35+E II, Graph 90+E, Graph Math+
- 77 : HP Prime G2
- 28 : TI-82 Advanced Edition Python, TI-83 Premium CE Edition Python
D7) Lignes et colonnes console PythonGo to top Nous avons donc vu plus haut la belle progression de l'éditeur en termes de nombre de lignes et colonnes de caractère visibles simultanément à l'écran.
Regardons maintenant la même chose mais du côté de la console
Python. Pour cela, prenons la fonction suivante :
- Code: Select all
def lgncols(l, c):
code_base = ord('z') - c - l + 2
chars = [str((i + 1) % 10) for i in range(c)]
print("".join(chars))
for i in range(1, l):
lgn = str(i + 1) + " "
lh = len(lgn)
if i > 1:
for j in range(c - lh):
lgn += chr(i + j + code_base + lh)
print(lgn)


L'appel
lgncols(l, c) permet de remplir sur la console
l lignes avec chacune
c colonnes de caractères.
Sur
Graph 90+E les plus petites valeurs permettant de remplir un écran dans la console étaient
7 lignes et
21 colonnes, valeurs donc caractéristiques de la console.
Sur
Graph Math+ nous avons une belle progression, il faut maintenant pas moins de
9 lignes et
38 colonnes pour remplir intégralement un écran dans la console ! 👍
On remarque en passant un bel avantage de
Casio, l'utilisation d'une police de caractères à largeur fixe, rendant fort aisée la conception d'interfaces texte en
Python.
D8) Caractères affichables en PythonGo to top Aussi bien sur Graph 90+E que Graph Math+, nous avons donc vu plus haut que l'outil de sélection de caractères et l'éditeur Python ne semblaient supporter que des caractères ASCII (7 bits), à l'exclusion donc de tous les caractères dits spéciaux dont les lettres accentuées.
Mais la console Python serait-elle capable d'afficher un éventail plus large de caractères ?
Nous pouvons utiliser la fonction
chr() qui permet d'obtenir une chaîne avec le caractère dont on a spécifié le code.
Sur les machines
Casio programmables en
Python, la fonction
chr() accepte des codes allant de 0 à 255
(0xFF), correspondant donc à de l'ASCII dit étendu
(8 bits).
Voici donc un script permettant d'afficher la table complète des 256 caractères gérés :
- Code: Select all
def dig2hex(n):
if n<10 : return str(n)
else: return chr(ord("A")+n-10)
def chars(n=256):
wcol = 16
ncol = 2
nlgn = n / wcol / ncol
schars="\a\b\t\n\v\f\r"
slgn = ""
for icol in range(ncol):
if len(slgn): slgn += "|"
slgn += " |"
for jcol in range(wcol):
slgn += dig2hex(jcol)
print(slgn)
for lgn in range(nlgn):
slgn = ""
for icol in range(ncol):
if len(slgn): slgn += "|"
slgn += dig2hex(lgn * ncol + icol)+"|"
for jcol in range(wcol):
n = lgn*wcol*ncol + icol*wcol + jcol
car = chr(n)
if car in schars:
car=" "
slgn+=car
print(slgn)
Et bien malgré la gestion en apparence de codes 8 bits
(pouvant faire croire à une gestion de l'ASCII étendu), nos gros efforts ne donnent rien.
Seuls
94 caractères non vides différents sont affichés dans la table, et en comptant 1 fois l'ensemble des affichages vide pour le caractère espace, cela donne très exactement les
95 caractères trouvés plus haut.
Bien dommage car les lettres accentuées nous seraient bien utiles en France. Si la
NumWorks souffre certes du même problème, ce n'est pas le cas des
TI-82 Advanced Edition Python et
TI-83 Premium CE Edition Python.
Voici ce que ça donne niveau classement en termes de nombre de caractères différents affichables, sans chiffrage lorsque disponible des caractères multi-octets car nous n'avons pas encore de protocole pour tous les compter :
rang | modèle | TOTAL | ASCII 7 bits | ASCII 8 bits | multi-octets |
1er | TI-Nspire CX II | 191+ | 96 | 95 | ? |
2nd | HP Prime | 159+ | 64 | 95 | ? |
3e | TI-83 Premium CE Edition Python
TI-82 Advanced Edition Python | 205 | 96 | 109 | 0 |
4e | NumWorks | 110 | 96 | 14 | 0 |
5e | Casio Graph 35+E II
Casio Graph 90+E
Casio Graph Math+ | 95 | 95 | 0 | 0 |
En
Python, on distingue les nombres entiers
(int) des nombres non entiers
(float). Il s'agit en effet de types d'objets distincts qui sont codés différemment.
Les nombres non entiers
(type float pour flottants), font l'objet d'un code dit en virgule flottante, que l'on peut exposer sous la forme suivante :
$mathjax$M\times 10^E$mathjax$
avec
M la mantisse et
E l'exposant.
Les capacités d'un moteur de calcul en virgule flottante dépendent ainsi des choix de codage effectués pour la mantisse et l'exposant.
Commençons par déterminer les plus petites et plus grandes valeurs autorisées pour l'exposant.
Pour la plus petite valeur d'exposant, l'idée est d'effectuer des divisions par 10 en boucle, jusqu'à réussir à annuler le résultat :
- Code: Select all
def expmin():
a, e = 1., 0
while a > 0:
a /= 10
e -= 1
return e + 1
L'exposant minimal possible est donc de
-323.
Pour la plus grande valeur d'exposant, l'idée est d'effectuer des multiplications par 10 en boucle, jusqu'à atteindre l'infini.
Normalement on peut tester si un résultat est infini avec la fonction
math.isinf()... sauf que cette fonction n'a apparemment pas été incluse dans la bibliothèque
math par
Casio. Alors il va nous falloir lui coder une remplaçante :
- Code: Select all
def isinf(n):
return n and n == n * 2
def expmax():
a, e = 1., 0
while not isinf(a):
a *= 10
e += 1
return e - 1
L'exposant maximul possible est donc de
308.
Enfin, reste à tester la précision de la mantisse :
- Code: Select all
def precm(b):
k, b = 0, float(b)
while 1 + b**-k-1 > 0:
k += 1
return k
Les appels
precm(10) et
precm(2) nous permettent de déterminer que les mantisses :
- permettent de coder jusqu'à 16 chiffres significatifs en base décimale
- permettent de coder jusqu'à 53 bits significatifs
Un codage caractéristique du des nombres flottants dits en double précision
(64 bits au lieu de 32 bits en comptant la mantisse, l'exposant et le signe), à égalité avec ce que donnait la
Graph 90+E ainsi que l'ensemble de la concurrence programmable en
Python.
Nous venons donc de voir qu'il manquait des choses à la bibliothèque
math de la
Graph Math+, à commencer par la fonction
isinf().
Tentons de chiffrer la chose avec le script suivant, ayant pour objectif de lister le contenu d'une bibliothèque et d'en compter les entrées utiles :
- Code: Select all
def clean(s):
for ss in ("<", ">", "'", "class ", "module "):
s = s.replace(ss, "")
return s
def module_entry_type(entry_name, module_name):
return clean(str(eval("type({:s}.{:s})".format(module_name, entry_name))))
def maxf(l, f):
return max([f(s) for s in l])
def rightPad(s, n):
while len(s) < n:
s += ' '
return s
def explmod(module):
module_name = module.__name__
lnames = dir(module)
lnames.sort()
dcol1 = maxf(lnames, len)
dcol2 = maxf([module_entry_type(name, module_name) for name in lnames], len)
n = len(lnames)
for f in lnames:
val = eval("{:s}.{:s}".format(module_name, f))
ignore = False
if f[:2] == "__" and f[-2:] == "__" and isinstance(val, str):
n -= 1
ignore = True
stype = module_entry_type(f, module_name)
sval = clean(str(eval("{:s}.{:s}".format(module_name, f))))
print("{:s} {:s} {:s} {:s}".format(ignore and '-' or '+', rightPad(f, dcol1), rightPad(stype, dcol2), sval))
return n
Après avoir importé la bibliothèque avec
import math, l'appel
explmod(math) nous liste et compte seulement
24 entrées utiles sur
Graph Math+.
À y regarder plus en détails, il nous manque pas mal de choses standard, comme :
- effectivement plusieurs fonctions de test relatives aux nombres : isfinite, isinf, isnan
- la fonction de troncature d'un nombre : trunc
- la fonction
copysign(x, y) appliquant le signe de y à la valeur absolue de x - les fonctions de conversion de mesure d'angle : degrees, radians
- la fonction
expm1(x) calculant de façon précise de exp(x)-1, utile lorsque x est proche de 0 - la fonction logarithmique de base 2 : log2
- les fonctions inverses de trigonométrie hyperbolique : acosh, asinh, atanh
- ce qui est relatif à la fonction d'erreur de Gauss : erf, erfc
- ce qui est relatif à la fonction gamma : gamma, lgamma
C'est quand même bien dommage car une bonne partie des absentes est clairement de niveau lycée et simplifierait de beaucoup le codage de certaines choses.
Il y avait très exactement le même problème sur
Graph 90+E, et
Casio n'a donc pas amélioré la chose.
- 42 entrées : NumWorks
- 41 entrées : TI-Nspire CX II, HP Prime
- 27 entrées : TI-82 Advanced Edition Python, TI-83 Premium CE Edition Python
- 24 entrées : Casio Graph 35+E II, Graph 90+E, Graph Math+
La
Graph Math+ dispose donc à ce jour de l'implémentation la plus pauvre de la bibliothèque
math, sans amélioration depuis la
Graph 90+E. Nous ignorons quel besoin a entrainé dès le départ ce besoin d'alléger la bibliothèque, alors que la
Graph 90+E était très loin d'être limitée matériellement par rapport à d'autres modèles.
Reprenons le script précédent mais cette fois-ci pour explorer la bibliothèque
builtins, fournissant toutes les fonctions disponibles par défaut en
Python.
Après avoir importé sous forme de bibliothèque avec
import builtins, l'appel
explmod(builtins) nous liste et compte seulement
83 entrées utiles sur
Graph Math+.
Ici on remarque de façon similaire le manque de nombre de types d'énumérateurs pour les boucles
(enumerate, filter, frozenset, reversed) ou encore de l'exception de type
UnicodeError.
- 97 entrées : TI-Nspire CX II, HP Prime
- 91 entrées : TI-82 Advanced Edition Python, TI-83 Premium CE Edition Python
- 88 entrées : NumWorks
- 83 entrées : Casio Graph 35+E II, Graph 90+E, Graph Math+
D12) Dimensions page graphique casioplotGo to top Mais l'application
Python de
Casio ne permet pas que des affichages dans la console, loin de là. Passons enfin à la bibliothèque caractéristique des calculatrices
Casio programmables en
Python,
casioplot.
Sur
Graph 90+E elle nous permettait de dessiner librement à l'écran pour le codage d'interfaces graphiques ou même jeux graphiques à l'aide de sa fonction
set_pixel(x, y, c).
De façon similaire, la fonction
get_pixel(x, y) permet de récupérer la couleur d'un pixel.
Les tracés sont effectués non pas dans la console
Python, mais sur une page-écran dédiée que nous appellerons
page graphique, affichée de façon indépendante. Précisons de plus que tout ce qui est tracé bénéficie d'un
double buffering. Tes tracés sont d'abord effectués de façon invisible hors écran sur la page dont nous venons de te parler, avant d'être tous montrés d'un coup par affichage de page lors du prochain appel à la fonction
show_screen().
C'est d'une part un gain en performances, la mémoire écran avec toutes ses contraintes n'ayant pas besoin d'être rafraichie à chacun de tes tracés. Et d'autre part, cela évite l'affichage de tracés intermédiaires pas toujours très esthétiques
(tracés partiels, traits de construction destinés à être effacés, clignotements, etc.).
La page graphique dont on contrôle les pixels est un rectangle, dont le coin supérieur gauche a pour coordonnées
(0;0). Mais quelles en sont les dimensions ?
On peut remarquer que la fonction
get_pixel(x, y) renvoie
None si appelée hors zone, par exemple avec des coordonnées négatives.
Voici donc un script exploitant cette astuce pour déterminer les dimensions en pixels de la zone graphique.
Dans un mouvement diagonal vers le bas et vers la droite, on va tester jusqu'à quand on peut :
- lire les pixels
- et inverser leurs valeurs
- Code: Select all
from casioplot import get_pixel, set_pixel, show_screen
bad_pixel = get_pixel(-2, -2)
def invert_color(c):
return [255 - c[k] for k in range(3)]
def is_pixel_writable(x, y):
if is_pixel_readable(x, y):
c0 = get_pixel(x, y)
set_pixel(x, y, invert_color(c0))
return get_pixel(x, y) != c0
return False
def is_pixel_readable(x, y):
try:
return get_pixel(x, y) != bad_pixel
except:
return False
def scr_test(x0, y0, dx0, dy0, test):
x, y, dx, dy = x0, y0, dx0, dy0
while not test(x, y):
x += dx
y += dy
if test(x, y - dy):
y = y0
elif test(x - dx, y):
x = x0
x0, y0 = x, y
x += dx
y += dy
while(dx or dy):
if not test(x - ((dx == 0) and dx0),y - ((dy == 0) and dy0)):
if test(x - ((dx == 0) and dx0), y - ((dy == 0) and dy0) - dy0):
dy = 0
elif test(x - ((dx == 0) and dx0) - dx0, y - ((dy == 0) and dy0)):
dx = 0
else:
dx, dy = 0, 0
x += dx
y += dy
return x0, y0, (x - x0) // dx0, (y - y0) // dy0
def scr_size():
xrd0, yrd0, xrd, yrd = scr_test(0, 0, -1, -1, is_pixel_readable)
xra0, yra0, xra, yra = scr_test(1, 1, 1, 1, is_pixel_readable)
xr0, yr0 = xrd0 - xrd + 1, yrd0 - yrd + 1
xr, yr = xra + xrd, yra + yrd
xw0, yw0, xw, yw = scr_test(xr0, yr0, 1, 1, is_pixel_writable)
show_screen()
print("at (" + str(xr0) + "," + str(yr0) + "): " + str(xr) + "x" + str(yr) + " readable pixels")
print("at (" + str(xw0) + "," + str(yw0) + "): " + str(xw) + "x" + str(yw) + " writable pixels")
return xr0, yr0, xr, yr, xw0, yw0, xw, yw
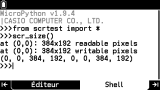
L'appel
scr_size() nous trouve donc sur
Graph Math+ une page graphique de
384×192 pixels, accessibles aussi bien en lecture qu'en écriture.
C'est très exactement ce qui était déjà proposé sur
Graph 90+E, et remarquons que c'est légèrement mieux que la zone graphique de
379×187 pixels partagée par les autres applications offrant une vue graphique.
- 320×240=76800 pixels : HP Prime
- 384×192=73728 pixels : Casio Graph 90+E, Graph Math+
- 320×222=71040 pixels : NumWorks
- 318×212=67416 pixels : TI-Nspire CX II
- 320×210=67200 pixels : TI-83 Premium CE Edition Python
- 128×64=8192 pixels : Casio Graph 35+E II
D13) Profondeur de couleurs casioplotGo to top 
Nous avons donc parlé du nombre de pixels allumables via la bibliothèque
casioplot, parlons maintenant de leurs couleurs.
Rappelons qu'en informatique un codage usuel est couleurs est le
RGB (ou RVB en Français), définissant une couleur selon ses coordonnées dans 3 composantes dites primaires : Rouge, Vert
(Green en Anglais) et Bleu. Les fonctions
casioplot attendent ou renvoient des couleurs sous la forme d'un tuple
(R, G, B) où chaque composante est une valeur entière allant de 0 à 255.
Il s'agit d'un format de couleurs
RGB-888, chaque composante avec 256 valeurs différentes nécessitant 8 bits, pour un total de 256×256×256=16'777'216 couleurs différentes nécessitant 24 bits.
Toutefois, si après un appel
set_pixel() tu vérifies la couleur prise par le pixel avec
get_pixel(), tu remarqueras qu'elle n'est pas toujours identique à ce que tu as demandé.
Si le
Python de la
Graph Math+ nous permet donc de travailler sur les couleurs en
RGB-888, il semble que le système d'exploitation de la calculatrice ou le matériel travaillent pour leur part dans un autre format de couleurs.
Tentons de voir ce qui se passe en affichant une mire de couleurs, c'est-à-dire un écran de test :
- Code: Select all
from casioplot import get_pixel, set_pixel, show_screen
def draw_vline(x, y1, y2, c):
for j in range(y2 - y1 + 1):
set_pixel(x, y1 + j, c)
def draw_hline(y, x1, x2, c):
for j in range(x2 - x1 + 1):
set_pixel(x1 + j, y, c)
def color8(j, v1, v2):
c = [0, 0, 0]
for b in range(3):
c[b] = j & 2**b and v1 or v2
return c
G_BRGHT, G_NONE, G_TLEFT = [i - 1 for i in range(3)]
G_HORIZ, G_VERT = range(2)
G_BLACK, G_WHITE = range(2)
def mire(gsens=G_TLEFT, gdir=G_HORIZ, gcol=G_BLACK, w=384, h=192):
"""trace une mire de couleurs selon les parametres suivants:
- gsens: activation et sens du degrade
* G_NONE : pas de degrade
* G_BRGHT: degrade vers bas/droite
* G_TLEFT: degrade vers le haut/gauche
- gdir: direction du degrade
* G_HORIZ: degrade horizontal
* G_VERT : degrade vertical
- gcol: couleur de destination du degrade
* G_WHITE: degrade vers le blanc
* G_BLACK: degrade vers le noir
- w: largeur du degrade en pixels
- h: hauteur du degrade en pixels
"""
if gdir: l1, l2, f = h, w, draw_hline
else: l1, l2, f = w, h, draw_vline
n = 8
for i in range(l1):
c1, c2 = 255, 0
if gsens != G_NONE:
if gcol:
c2 = 255 * (l1 - 1 - gsens*i % l1) // (l1 - 1)
else:
c1 = c1 * (gsens*i % l1) // (l1 - 1)
for j in range(n):
f(i, j * l2 // n, (j + 1) * l2 // n - 1, color8(j, c1, c2))
show_screen()
Avec les appels
mire(G_TLEFT, G_HORIZ, G_BLACK) ou
mire(G_TLEFT, G_HORIZ, G_WHITE), nous choissons d'afficher un dégradé vers le noir ou vers le blanc, des couleurs RGB primaires et secondaires :
Si tu regardes bien pour les dégradés vers le noir, tu remarqueras que toutes les couleurs utilisant la composante verte
(Vert, Jaune, Cyan et Blanc), présentent 2 fois plus de teintes intermédiaires, produisant des dégradés plus esthétiques.
Mais nos sens nous trompent selon Descartes, aussi le fameux
"je vois sur la figure" ne constitue en rien une démonstration, c'est-à-dire une preuve valide pour un matheux.
Alors dans cas, comptons, à l'aide du script suivant :
- Code: Select all
from casioplot import get_pixel, set_pixel, show_screen
from math import log
def rightPad(s, n):
while len(s) < n:
s += ' '
return s
def scr_colors():
cnames = ('red', 'green', 'blue')
v = 0
set_pixel(0, 0, [v] * 3)
cget0 = get_pixel(0, 0)
lbits = [0] * 3
while 0 in lbits:
v += 1
set_pixel(0, 0, [v] * 3)
cget = get_pixel(0, 0)
for i in range(3):
if not lbits[i] and cget[i] != cget0[i]:
n = 256 // v
lbits[i] = int(log(n, 2))
print("{:s} channel: {:d} values on {:d} bits".format(rightPad(cnames[i], 5), n, lbits[i]))
print("format : RGB-{:d}{:d}{:d}".format(lbits[0], lbits[1], lbits[2]))
return lbits
Nous détectons effectivement :
- 32 affichages différents possibles pour les composantes rouge et bleu, soit un codage sur 5 bits
- mais 64 affichages différents possibles pour la compossante verte, soit un codage sur 6 bits
Si le code
Python nous fait donc penser en
RGB-888, il semble que le système et/ou matériel de la
Graph Math+ travaille pour sa part en
RGB-565, un codage sur 16 bits permettant un affichage de 32×64×32=65536 couleurs différentes.
Pas d'amélioration donc ici, c'était déjà ce que permettait la
Graph 90+E, et c'est d'ailleurs le codage usuel sur la quasi totalité des calculatrices graphiques couleur programmables en
Python.
C'est un codage très confortable pour réaliser des activités permettant de mieux comprendre le codage des couleurs en informatique, des interfaces graphiques ou même des jeux !
- 24 bits (16'777'216 couleurs) : HP Prime
- 16 bits (65'536 couleurs) : TI-83 Premium CE Edition Python, NumWorks, Casio Graph 90+E, Graph Math+
D14) Colonnes et lignes casioplot avec drawstringGo to top Passons maintenant à une autre fonction de la bibliothèque
casioplot,
draw_string().
Cette fonction te permet d'écrire du texte non pas dans la console
Python, mais sur la page graphique avec donc l'ensemble de tes autres tracés.
De spécification
draw_string(x, y, t, c=(0,0,0), p="medium"), la fonction attend en paramètres :
- x et y : les coordonnées en pixels du coin supérieur gauche du cadre de texte
- t : le texte à écrire dans le cadre
- c : la couleur d'écriture du texte, et par défaut
(0,0,0) pour du noir si non spécifié - p : la police de texte à utiliser avec comme valeurs autorisées 'large', 'medium' et 'small', et par défaut 'medium' si non spécifié
Le cadre du texte est pour sa part totalement transparent et ne laisse aucune trace, ce qui permet de réaliser fort facilement de beaux effets de texte !
- Code: Select all
from casioplot import *
from math import sin, cos, pi
SCREEN_W, SCREEN_H = 384, 192
def fill_rect(x, y, w, h, c):
for dy in range(y, y+h):
for dx in range(x, x+w):
set_pixel(dx, dy, c)
def draw_string8(x, y, t, c, p, cb, wb):
for dy in range(-wb, wb + 1, wb):
for dx in range(-wb, wb + 1, wb + (not dy and wb)):
draw_string(x + dx, y + dy, t, cb, p)
def lighten_color(c, f):
f = max(f, 0)
return [v + int(f * (255 - v)) for v in c]
TEXT = ' '.join([c for c in 'CASIO'])
COLOR = (1, 50, 152)
COLOR_WHITE = (255, 255, 255)
MAX_STEPS = 64*2
R = 36
FACT = .75
fill_rect(0, 0, SCREEN_W, SCREEN_H, COLOR)
def loop():
x0, y0 = 2 * R + 2, SCREEN_H // 2 - 10
steps = 1
j = 0
dj, ds = 0, 1
while steps:
for i in range(-1, steps + 1):
c = lighten_color(COLOR, i / steps)
a = (i + j) * pi / 180 * FACT
x = x0 + 2*R*cos(a)
y = y0 + R*sin(a)
draw_string8(int(x), int(y), TEXT, c, 'large', c, 2)
draw_string8(int(x), int(y), TEXT, COLOR_WHITE, 'large', COLOR, 1)
draw_string(int(x), int(y), TEXT, COLOR_WHITE, 'large')
if j + dj > 360 / FACT - steps and steps:
ds = -1
elif not j and steps + ds >= MAX_STEPS:
dj, ds = 1, 0
j += dj
steps += ds
show_screen()
while True:
loop()
Pour positionner correctement des éléments de texte sur l'affichage de tes interfaces graphiques ou même jeux graphiques, tu as besoin de connaître les dimensions de chacune des 3 polices.
Alors creusons la question à l'aide du script suivant, qui va compter le maximum de pixels utilisés horizontalement et verticalement par les différents caractères affichables de la calculatrice :
- Code: Select all
from casioplot import *
SCREEN_W, SCREEN_H = 384, 192
C_BLACK = (0, 0, 0)
def font_size(font, maxw=25, maxh=25):
w, h = 0, 0
x1, x2 = 0, 0
y1, y2 = 0, 0
for n in range(32, 127):
c = chr(n)
clear_screen()
draw_string(0, 0, c, C_BLACK, font)
for y in range(maxh):
for x in range(maxw):
if get_pixel(x, y) == C_BLACK:
x2 = max(x, x2)
y2 = max(y, y2)
else:
x1 = min(x, x1)
y1 = min(y, y1)
w = x2 - x1
h = y2 - y1
print("left margin :", x1)
print("top margin :", y1)
print("width :", w)
print("height :", h)
return x1, y1, w, h
font_size('large') nous indique que cette police nécessite au maximum :
- 22 pixels en hauteur
- 17 pixels en largeur de caractère
Pour voir, tentons donc maintenant de remplir la page graphique de plusieurs lignes de texte à l'aide du script suivant, nous permettant de préciser la hauteur de police à utiliser :
- Code: Select all
from casioplot import *
def lgncols(l, c, font, fh):
clear_screen()
y = 0
col = (0, 0, 0)
code_base = ord('z') - c - l + 2
chars = [str((i + 1) % 10) for i in range(c)]
draw_string(0, 0, "".join(chars), col, font)
for i in range(1, l):
lgn = str(i + 1) + " "
lh = len(lgn)
if i > 1:
for j in range(c - lh):
lgn += chr(i + j + code_base + lh)
y += fh
draw_string(0, y, lgn, col, font)
show_screen()


Avec la police
'large', nous pouvons au choix :
- mettre 22 pixels entre 2 lignes de texte successives, pour un affichage sans chevauchement, et on peut alors avoir presque 9 lignes de texte par écran
- ou bien mettre 23 pixels entre 2 lignes successives pour avoir un interligne d'au moins 1 pixel de hauteur, et on peut alors avoir 8,5 lignes par écran
Notons au passage que la police
'large' semble être à largeur fixe, avec toujours
18 pixels entre 2 caractères successifs d'une ligne, et donc
21,5 colonnes par écran.

De façon similaire, testons la police
'medium'.
Elle nécessite au maximum :
- 16 pixels en hauteur
- 13 pixels en largeur de caractère
Pour enchaîner plusieurs lignes de texte, on peut donc les espacer :
- de 16 pixels pour éviter les chevauchements, et on peut alors avoir 12 lignes de texte par écran
- ou bien 17 pixels, pour avoir un interligne d'au moins 1 pixel de hauteur, et on peut alors avoir 11,5 lignes par écran
Notons qu'ici la police
'medium' n'est pas à largeur fixe.
Enfin, terminons avec la police
'small'.
Elle nécessite au maximum :
- 9 pixels en hauteur
- 7 pixels en largeur de caractère
Pour enchaîner plusieurs lignes de texte, on peut donc les espacer :
- de 9 pixels pour éviter les chevauchements, et on peut alors avoir 19,5 lignes de texte par écran
- ou bien 10 pixels pour avoir un interligne d'au moins 1 pixel de hauteur, et on peut alors avoir 17,5 lignes par écran
La police
'small' n'est elle non plus pas à largeur fixe.
Avec les formidables capacités graphiques que nous venons d'évoquer, il était possible sur
Graph 90+E de créer des jeux graphiques.
Toutefois, la machine souffrait de plusieurs limitations assez sérieuses.
Une de ces limitations était l'absence d'une fonction permettant de détecter les pressions de touches clavier.
Nous n'avions que 2 contournements pour permettre à un jeu de récupérer les actions du joueur :
- soit par appel à la fonction
input(), bloquante et donc mettant tout le jeu en pause, convenant plutôt à des jeux se jouant au tour par tour - soit par interception de l'exception KeyboardInterrupt déclenchée par la pression de la touche
AC/ON
, cette fois-ci certes utilisable pour des jeux se jouant en temps réel, mais à la condition qu'ils puissent se jouer avec 1 seule touche
Nous étions donc limités à des types assez restreints de jeux. Il restait possible de créer de très belles choses, mais il fallait bien penser son jeu en amont afin que le codage soit faisable. Nous pouvons citer les jeux
Flappy Bird,
Etiord City ou encore
Gravity Guy créés suite à une
commande de
Casio France, des jeux ayant tous la particularité d'être jouables avec 1 seule touche :
Et bien nous avons une formidable nouvelle à t'apprendre. Cela faisait des années que nous la réclamions à Casio, et sur Graph Math+ la bibliothèque casioplot a enfin été étendue avec une nouvelle fonction getkey() permettant d'identifier les touches tapées par l'utilisateur. Nous avons donc enfin droit aux jeux Python se jouant à plusieurs touches ! 👍
De plus Casio a vraiment été au top, la fonction getkey() étant non bloquante. Ne mettant pas le jeu en pause, la fonction est donc utilisable aussi bien pour les jeux au tour par tour que les jeux en temps réel ! 👍
Le développement de jeux Python sur Graph Math+ va donc pouvoir atteindre un tout nouveau niveau ! 🎉
La fonction
getkey() étant non bloquante, comment faire si tu as besoin d'attendre une pression de touche ?
Sachant que la fonction renvoie
None si aucune touche n'est pressée, il va te falloir attendre avec une boucle :
- Code: Select all
from casioplot import getkey
def waitkey():
key = None
while key == None:
key = getkey()
return key
On remarque en passant que l'on ne peut pas détecter de pression sur certaines touches via la fonction
getkey() :
- la touche
ON
est ignorée - et la touche
AC
interrompt le script
Mais pour pouvoir commencer à développer, il te faut connaître les codes des différentes touches du clavier. Concevons une petit interface afin de rapidement tous les découvrir :
- Code: Select all
from casioplot import *
from math import sqrt
SCREEN_W, SCREEN_H = 384, 192
FONT, FONT_W, FONT_H = 'medium', 13, 16
C_BLACK = (0, 0, 0)
C_RED = (255, 0, 0)
C_BLUE = (0, 0, 255)
C_GRAY = (191, 191, 191)
C_WHITE = (255, 255, 255)
C_MAGENTA = (255, 0, 255)
def waitkey():
key = None
while key == None:
key = getkey()
return key
def keycolor(row, col):
if row >= 3 or row == 2 and col >= 2 and col != 3: return C_BLACK
elif row == 2 and col == 0: return C_BLUE
elif row == 2 and col == 1: return C_RED
else: return C_GRAY
ROWS1, COLS1 = 5, 6
ROWS2, COLS2 = 4, 5
ROWS = ROWS1 + ROWS2
DKEY1 = SCREEN_H // COLS1
RKEY1 = DKEY1//2 - 1
DKEY2 = SCREEN_H // COLS2
RKEY2 = DKEY2//2 - 1
def getcols(row):
return row < ROWS1 and COLS1 or COLS2
def getxyr(row, col):
x = min(row, ROWS1)*DKEY1 + max(row - ROWS1, 0)*DKEY2
cols = getcols(row)
dkey = row < ROWS1 and DKEY1 or DKEY2
y = (cols - col - 1)*dkey
r = row < ROWS1 and RKEY1 or RKEY2
return x + dkey//2, y + dkey//2, r
def draw_line(x, y, w, c):
for dx in range(w):
set_pixel(x + dx, y, c)
def fill_circle(x0, y0, r, c):
for ry in range(-r, r + 1):
rx = sqrt(r**2 - ry**2)
x = int(round(x0 - rx, 0))
rx = abs(x - x0)
draw_line(x, y0 + ry, 2*rx + 1, c)
def draw_key(row, col, color=None, label=None):
x, y, r = getxyr(row, col)
if not color:
color = keycolor(row, col)
fill_circle(x, y, r, color)
if label:
draw_string(x - FONT_W*len(label)//2, y - FONT_H//2, label, C_WHITE, FONT)
for row in range(ROWS):
for col in range(getcols(row)):
draw_key(row, col)
for row in range(ROWS):
for col in range(getcols(row)):
if not (row, col) in ((0, 0), (5, 4)):
draw_key(row, col, color=C_MAGENTA)
show_screen()
k = waitkey()
draw_key(row, col, label=str(k))
show_screen()
L'interface t'indique successivement en couleur magenta chacune des touches clavier à presser
(à l'exception de ON
et AC
comme déjà dit), et t'en affiche alors le code sur la touche en question.
Nous finissons par obtenir la carte complète des codes de touches clavier :
Et bien nous nous rendons compte que le codage est en fait extrêmement logique et donc facile à retenir. Chaque touche est identifiable par un code à 2 chiffres
RC:
- où R est le numéro de rangée de la touche au clavier (rangée numérotée de haut en bas en partant de 1 )
- et C est le numéro de colonne de la touche sur la rangée (colonne numérotée de gauche à droite en partant de 1)
Si l'on suit cette même logique, la touche
AC
aurait pour code
65 (6e rangée en partant du haut, et 5e colonne de la rangée en partant de la gauche).
Si jamais tu en avais besoin, on peut même s'amuser à étendre la fonction
getkey() pour détecter également la touche
AC
:
- Code: Select all
from casioplot import getkey
_getkey = getkey
def getkey():
try:
return _getkey()
except :
return 65
def waitkey():
try:
key = None
while key == None:
key = getkey()
return key
except:
return 65
Si il y a certes eu des progrès très significatifs démultipliant les possibilités de création de jeux
Python graphiques sur
Graph Math+, il subsiste encore une contraire majeure.
La bibliothèque
casioplot ne fournit que les 2 fonctions de tracé que nous venons de couvrir :
set_pixel() pour allumer 1 pixel, et
draw_string() pour écrire du texte. Pas d'amélioration donc par rapport à la
Graph 90+E.
En l'absence de toute autre fonction de tracé, les jeux nécessitant un rafraîchissement de tout l'écran
(par exemple les jeux 3D) ne peuvent pas bénéficier d'une optimisation de leur affichage. Ils sont obligés d'effectuer 384×192=73728 appels à
set_pixel() à chaque rafraîchissement de l'écran, ce qui prend un temps certain, et conduit à un
framerate absolument catastrophique.
Prenons par exemple la fonction de remplissage de rectangle suivante :
- Code: Select all
def fill_rect(x, y, w, h, c):
for dy in range(y, y+h):
for dx in range(x, x+w):
set_pixel(dx, dy, c)
Sur
Graph 90+E, un remplissage intégral de l'écran par exemple avec
fill_rect(0, 0, 384, 192, (0, 0, 255)) était tout sauf instantané, prenant autour de 2 secondes, ce qui te pouvait laisser espérer une expérience de jeu avec un
framerate de
0.5 fps, et encore dans le meilleur des cas c'est-à-dire sans aucun autre calcul.
Une voie d'optimisation du rafraîchissement d'un jeu est justement de le décomposer en affichages de plusieurs rectangles remplis à chaque fois d'une couleur unie. Selon le type de graphismes du jeu, cela peut donner un nombre hautement réduit d'appels à une fonction
fill_rect().
Bien évidemment ici notre fonction
fill_rect() est codée en
Python et réalisera donc malgré tout à son tour les appels à
set_pixel() pour chacun des 73728 pixels de la page graphique.
Mais si
Casio pouvait nous coder cette fonction
fill_rect() de façon native et l'intégrer à la bibliothèque
casioplot, cela nous démultiplierait une nouvelle fois les possibilités pour les interfaces graphiques et jeux graphiques.

Passons à l'application
Base-N.
Elle vise à réaliser des conversions ou calculs faisant appel à d'autres bases numériques que la base décimale.
Cette application n'adopte pas la nouvelle répartitions par onglets, concentrant tout sur un unique écran.
La Graph 90+E permettait déjà de faire appel à différentes bases numériques pour tes calculs, mais c'était une fonctionnalité relativement cachée et fort mal intégrée.
Depuis l'application de calcul historique il fallait aller dans les réglages pour modifier le paramètre Mode sur une autre valeur que Comp.
Les conversions et calculs avec des bases non décimales devenaient alors possibles, mais au prix d'un changement radical du comportement de l'application de calcul, désactivant la saisie naturelle, l'accès à nombre de fonctions scientifiques au clavier, ou encore la possibilité de remonter dans l'historique des calculs.
L'écran de calcul devenait donc temporairement incapable de permettre autre chose que des conversions et calculs simples avec des bases non décimales. Pour retrouver un fonctionnement normal il fallait retourner défaire le réglage en question, doublant donc la lourdeur de la chose.
Un fonctionnement donc extrêmement déconcertant et lourd pour l'utilisateur.

Avec la
Graph Math+ c'en est fini de tout ça.
La toute nouvelle application
Base-N nous apporte en effet une toute nouvelle interface dédiée à ce type de calculs !
De haut en bas on distingue :
- la ligne de saisie pour tes nombres ou calculs
- la base numérique à utiliser pour les nombres de ta saisie dont tu ne précises pas la base, modifiable avec la touche
FORMAT
comme clairement indiqué (tu peux basculer entre hexadécimal, décimal, octal et binaire) - et enfin le résultat de la saisie, automatiquement converti pour un affichage simultané dans chacune des 4 bases numériques précédentes !
On note au passage au nombre constant de chiffres affichés que cette application permet de travailler avec des nombres de 32 bits au maximum
(c'est-à-dire 4 octets).

En base hexadécimale, pour la saisie de chiffres supérieurs à 9, c'est-à-dire des lettres
A à
F, tu peux utiliser le menu
CATALOG
avec son entrée
"Valeur hexadécimale".
Ces saisies hexadécimales te sont également possibles au clavier, à l'aide des touches de fonction alphabétique
A à
F.

Toutefois, problème avec le clavier. Il te
faudra en effet presser les touches ayant pour fonction alphabétique
A à
F, mais directement sans activer le modificateur
ALPHA
. Si tu actives le modificateur
ALPHA
, ta saisie sera ignorée.
Nous comprenons cette spécificité, évident de multiplier les pressions de la touche
ALPHA
dans un contexte où les lettres
A à
F interviendront souvent, mais le problème est que cela change sans avertissement les règles de fonctionnement du clavier, et que ce n'est donc pas intuitif pour les utilisateurs. Sûrement que nombre d'entre eux à leur première utilisation vont taper
ALPHA
puis se rendre compte que cela ne fonctionne pas.
L'effort est donc appréciable et plein de bonnes intentions, mais il aurait fallu faire en sorte que la saisie fonctionne dans les deux cas, avec et sans le modificateur
ALPHA
activé.

Puisque nous avons évoqué le menu
CATALOG
, profitons-en car il permet d'aller beaucoup plus loin.
Nombre d'opérations binaires
(dans le sens bit à bit) sont proposées sous l'entrée
"Opération logique" :
- Neg : négatif/opposé (complément à 2)
- Not : non/négation (complément à 1)
- and : et
- or : ou
- xor : ou exclusif
- xnor : non ou exclusif

Enfin, si tu souhaites effectuer un calcul faisant intervenir des nombres écrits dans différentes bases, c'est également possible. Il te suffit pour cela de préfixer les nombres ne correspondant pas au réglage courant afin d'en indiquer la base
(avec les préfixes b, d, o et h disponibles au catalogue sous l'entrée "Préfixe de base").
E2) Application Mémoire : Capacités, formats de fichiers supportés et point sur les applications additionnellesGo to top 
L'application
Mémoire présente 2 onglets :
- Mémoire princi (affiché par défaut)
- Mémoire stock
L'onglet
Mémoire princi concerne la mémoire principale.
Mais déjà avant tout, qu'est-ce que c'est ? Il s'agit de l'espace qui est réservé en mémoire
RAM pour le stockage des variables définies ou modifiables par l'utilisateur. On peut citer comme éléments de taille significative y étant usuellement stockés les matrices, vecteurs, listes ou encore programmes en langage
Casio Basic.
Pour obtenir l'espace libre maximal pouvant être rendu disponible pour l'utilisateur, il suffit de supprimer tous les éléments y étant présents.
La
Graph 90+E offrait jusqu'à
61.440 Ko d'espace disponible en mémoire de stockage, et il n'y a pas de changement sur la
Graph Math+.
Précisons que 2 éléments de la mémoire principale ne sont toutefois jamais effaçables, même en déclenchant une réinitialisation de la calculatrice,
ALPHA_MEM et
SETUP occupant respectivement
696 et
200 octets.
En supposant que l'écran en question nous liste bien tout, par addition de ces consommations à l'espace libre on obtient alors la capacité de la mémoire principale :
62,336 Ko.
L'onglet
Mémoire stock concerne la mémoire de stockage. C'est ici l'espace qui est réservé en mémoire
Flash pour le stockage des fichiers. Ici il s'agit d'un système de fichiers complet, librement organisable par l'utilisateur selon différents dossiers.
Les
Graph 90+E,
fx-CG50 et
fx-CG50AU utilisaient une puce
Flash de
32 Mio de capacité.
L'espace était découpé en 2 partitions : une pour le système d'exploitation, et une pour la mémoire de stockage.
Après vidage de son contenu, cet espace de stockage en mémoire
Flash indiquait comme capacité :
- 16,248 Mo sur Graph 90+E et fx-CG50
- 4,714 Mo sur le modèle australien fx-CG50AU
Bien qu'utilisant dans tous les cas une puce
Flash de
32 Mio (avec une partition de 16 Mio réservée au système d'exploitation), la capacité était donc bridée sur la
fx-CG50AU par rapport à une réglementation en Australie interdisant aux candidats de disposer de trop d'espace mémoire sur leur calculatrice.

Rien à vider sur
Graph Math+, la mémoire de stockage nous est venue intégralement vide. Malgré cela, de façon totalement inattendue, la capacité de la mémoire de stockage semble avoir été drastiquement réduite sur
Graph Math+, l'espace libre indiqué n'étant plus que de
4,717 Mo, c'est-à-dire très exactement la même valeur que sur
fx-CG50AU.
C'est à peine 30% de ce que nous avions sur
Graph 90+E, et c'est extrêmement surprenant.
Si les fonctionnalités annoncées pour la mise à jour majeure de 2025 sont destinées à être apportées sous la forme d'applications intégrées au système d'exploitation, on peut certes imaginer que ce dernier ait désormais besoin d'une partition plus large que
16 Mio.
Mesurons donc ce qu'occupent les actuelles applications additionnelles apportant des fonctionnalités équivalentes sur
Graph 90+E :
- 1,823 Mo : Physium (tableau périodique + bibliothèque de constantes physiques)
- 329 Ko : Graphe3D
- 406 Ko : Sim Prob
- 771 Ko : Geometrie
Dans le pire des cas, si jamais il ne restait plus d'espace utilisable pour du code exécutable dans la partition système de
16 Mio,
Casio aurait donc eu besoin de trouver juste dans les
3,3 Mo d'espace supplémentaire. Si certes il faut se garder une marge pour d'éventuels autres ajouts de fonctionnalités majeures lors de mises à jour futures non encore annoncées, nous avoir supprimé plus de
11,5 Mo nous paraît totalement excessif.
Autre hypothèse,
Casio aurait peut-être voulu faire un modèle
fx-CG100 international qui serait directement autorisé en Australie, éliminant donc le besoin de s'embêter à produire un modèle spécifique pour ce pays. Certes, nous avons vu qu'un modèle similaire spécifique à l'Australie était prévu, la
fx-1AU GRAPH, mais nous n'attendons pas sa sortie avant la rentrée 2025 au plus tôt. Peut-être
Casio a-t-il changé d'avis entre temps. Si la
fx-1AU GRAPH ne sortait finalement pas, la
fx-CG100 internationale pourrait directement être commercialisée à la place en Australie puisque dépourvue d'un espace de stockage jugé trop important selon les critères du pays en question. Nous verrons d'ici la rentrée 2025 ce qu'il en est.
Dernière hypothèse,
Casio a peut-être simplement cherché à minimiser les coûts de développement, surtout si c'est la même puce
Flash de
32 Mio qui est utilisée. Puisqu'il y avait besoin de réduire l'espace de stockage afin de laisser davantage de place pour la partition système, et que du code existait déjà en ce sens pour le modèle
fx-CG50AU,
Casio aurait apparemment pu choisir de réutiliser directement ce dernier, plutôt que d'avoir à écrire du code gérant un tout nouveau partitionnement intermédiaire de la mémoire
Flash de
32 Mio. Si certes remplacer une taille de partition éventuellement plusieurs fois dans le code n'est a priori pas complexe, rappelons qu'une mémoire
Flash ça s'use avec le nombre de réécritures aux mêmes endroits. Il y a toute une stratégie certes par partitions mais aussi par secteurs et par blocs, et réutiliser l'ancien code de partitionnement
fx-CG50AU éliminait certes le petit effort de modification du code, mais surtout le coût de vérification de la correction du code, ainsi que de la fiabilité et surtout durabilité de la puce
Flash dans le cadre de cette modification. En effet, l'ancien code avait l'avantage d'avoir déjà fait l'objet de cette validation pour la puce
Flash de
32 Mio en question.
Ces deux dernières hypothèses nous semblent être les plus probables, et concernant la dernière nous allons voir dans un moment si c'est bien la même puce
Flash de
32 Mio qui est utilisée.
Le mode examen qu'est-ce que c'est ? C'est un mode de fonctionnement spécial de ta calculatrice, dont l'activation est exigée en France depuis la session d'examens 2020, et régi par la
circulaire n°2015-178 du 1er octobre 2015. L'une des caractéristiques de ce mode est d'interdire la consultation de toute donnée qui auraient été préchargée en mémoire avant l'activation du mode examen. Il est donc destiné à être activé au tout début d'une épreuve.
Le bon fonctionnement du mode examen doit être indiqué par le clignotement régulier et permanent
(même calculatrice éteinte) d'une diode dédiée présente sur la tranche supérieure de la calculatrice.
Sur la
Graph 90+E, l'invocation du mode examen nécessitait d'allumer la calculatrice en maintenant les touches
7
et
COS
enfoncées. Moyen mnémotechnique, en fonctions alphabétiques ces touches correspondaient respectivement à
M et
E, ce qui donnait
Mode Examen. Mais cela n'en restait que peu accessible pour qui ne connaissait pas cette astuce ou ne réalisait pas cette manipulation assez souvent, et ne lisait pas l'aide en ligne du mode examen disponible dans la calculatrice.


Avec la
Graph Math+ fini les ennuis,
Casio a eu l'idée lumineuse de créer une toute nouvelle application
Mode examen dédiée, une application fort loquace qui te le laissera jamais tomber avec son aide en ligne exhaustive ! 👍
Cette application n'est pas organisée en onglets, se présentant comme un simple menu, permettant une activation claire, simple et rapide du mode examen :

Attention car comme sur
Graph 90+E, le mode examen de la
Graph Math+ est plus sévère que ce qu'exige la réglementation.
Il ne se contente pas de bloquer l'accès aux données préchargées en mémoire, mais interdit également tout calcul vectoriel, comme indiqué clairement entre bien d'autres choses dans l'aide en ligne évoquée.
Comme tu peux le constater, en mode examen toutes les entrées ou fonctions relatives au calcul vectoriel disparaissent des menus :
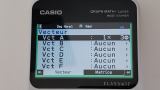
Il te sera toujours possible de définir des vecteurs, mais sans accès désormais au préfixe
Vct il te sera strictement impossible de faire quelque chose avec.
Précisons toutefois que tu conserves l'accès au calcul matriciel. Il te reste donc possible de définir de définir tes vecteurs sous la forme de matrices
(à 1 seule ligne ou 1 seule colonne) et d'effectuer des calculs simples dessus : addition, soustraction. Pas de possibilité simple d'effectuer un produit vectoriel. Toutefois en faisant preuve d'un peu d'astuce, le produit scalaire de 2 vecteurs est pour sa part accessible en tant que produit de 2 matrices :
À notre connaissance
Casio interdit le calcul vectoriel dans le mode examen français, parce que le constructeur tient à ce que ses modèles français puissent être utilisés aux épreuves du Baccalauréat International, où ces fonctionnalités sont interdites.
À notre sens c'est bien dommage, de brider ainsi la totalité des lycéens et lycéennes de France juste pour la petite minorité passant le Baccalauréat International. Rappelons qu'aucun concurrent n'interdit le calcul vectoriel en mode examen sur ses modèles français.


Une fois le mode examen activé, son bon fonctionnement peut être vérifié par les surveillants de 4 façons différentes, pas moins :
- déjà, à l'écran d'accueil de l'application Mode Examen, ce dernier précisant de plus :
- la configuration du mode examen (France dans notre cas) et donc sa conformité avec la réglementation
- à titre informatif la version système, au cas où des failles aient été identifiées et soient corrigées dans une version plus récente
- un drapeau R bleu clignotant en haut à droite de l'écran (de façon rapide puis ralentie après 15 minutes, une façon de vérifier si le mode examen a bien été activé en début d'épreuve et pas avant)
- une diode rouge clignotante sur la tranche supérieure de la calculatrice, le clignotement se poursuivant même calculatrice éteinte, avec une période constante de 2 secondes
- une bordure de couleur autour de l'écran, vert dans le cas de la configuration pour la France, seule couleur garantissant la conformité de la configuration du mode examen avec la réglementation française
Par rapport à ce dernier point précisons que la bordure verte, présente sur les bords gauche, droit et inférieur de l'écran, utilise de petites bandes de pixels qui ne sont jamais utilisées par l'interface, restant toujours de couleur noire en dehors du mode examen :
- bandes de 6 pixels de large à gauche et à droite
- bande de 8 pixels de haut en bas

Pour les petits malins qui activent leur mode examen avant leur épreuve afin de pouvoir arriver à cette dernière avec une mémoire non vide
(la mémoire n'étant vidée qu'au moment de l'activation),
Casio a prévu plusieurs parades.
D'une part, aucun besoin pour les surveillants de s'embêter à trouver une calculatrice compatible ou configurer en urgence un ordinateur pour désactiver le mode examen, l'application propose dans ce cas la possibilité directe de réactiver le mode examen, c'est-à-dire de vider à nouveau toute éventuelle donnée mémoire !
D'autre part, 15 minutes après l'activation du mode examen, la période de clignotement du drapeau
R à l'écran change, passant de 1 à 2 secondes. Si cette période de 2 secondes est constatée durant les premières 15 minutes d'une épreuve, c'est que d'une façon ou d'une autre il y a eu tentative de fraude.
Précisons plusieurs restrictions du mode examen dans son implémentation par
Casio :
- l'éclairage de l'écran peut être diminué mais jamais éteint complètement, ce qui permet une meilleur visibilité sur ce que font les candidats par les surveillants
- toutes les données saisies pendant l'examen, y compris celles qui habituellement vont en mémoire de stockage Flash comme les fichiers de scripts Python, sont stockés obligatoirement en mémoire principale RAM, ce qui te limite donc à 64K de données
- toutes les données saisies en examen sont perdues en cas de :
- redémarrage de le calculatrice (bouton RESTART au dos ou plantage)
- rupture de l'alimentation (piles à plat, retrait d'une pile, changement de piles)
Désactiver le mode examen c'est important car, comme l'application te le rappelle lors de son activation, il consomme beaucoup d'énergie. Ce n'est pas la petite diode clignotante qui a une consommation aussi extraordinaire. En fait en mode examen ta calculatrice ne s'éteint jamais complètement. L'écran s'éteint certes, mais le processeur reste pour sa part éveillé afin de continuer à piloter le clignotement de la diode. Or les deux éléments de la calculatrice les plus gourmands en énergie sont justement l'écran et le processeur, ce dernier arrivant d'ailleurs de loin en première position lorsque occupé par un calcul.
Sauf que désactiver le mode examen d'une
Graph 90+E c'était tout sauf trivial, cela ne se devinait pas.
Pour désactiver le mode examen à partir d'une autre calculatrice, il te fallait :
- trouver une autre calculatrice Casio, couleur ou monochrome, mais n'étant pas en mode examen
- relier les 2 calculatrices à l'aide du câble mini-Jack 2.5mm
- ouvrir l'application Lien/LINK sur les 2 calculatrices
- toujours sur les 2 calculatrices, vérifier que le type de câble est bien réglé sur "3 pins/broches" et non USB (et à défaut, régler le bon câble)
- sur la calculatrice en mode examen, la mettre en mode réception de données
- enfin sur l'autre calculatrice, selon le cas :
- sur une machine disposant du mode examen, lancer sous l'onglet EXAM le déverrouillage du mode examen
- ou sinon, dans tous les cas, effectuer les manipulations pour transférer n'importe quelle donnée présente en mémoire
Pour désactiver le mode examen à partir d'un ordinateur
(ou de n'importe quel appareil hôte USB actif : tablette, smartphone OTG, ...), il te fallait :
- connecter ta calculatrice en mode examen à l'ordinateur
- sur la fenêtre popup de la calculatrice, choisir le mode de connexion "clé USB"
- dans l'espace de stockage apparaissant sur l'ordinateur, réaliser n'importe quelle manipulation en faisant varier l'espace libre (création, copie ou suppression d'un fichier non vide)
Et bien, superbes améliorations de la désactivation du mode examen sur
Graph Math+.
Pour la désactivation du mode examen à partir d'une autre calculatrice, pas besoin de mettre la
Graph Math+ en mode réception de données
(ce qui de toutes façons est impossible sans l'application Lien), et pas de type de câble à régler non plus. La
Graph Math+ semble tout simplement écouter en permanence toute arrivée de donnée sur son port
mini-Jack 2.5mm ! 👍

Pour la désactivation du mode examen à partir d'un hôte
USB actif
(ordinateur, tablette, smartphone OTG, ...), plus besoin de s'embêter à réaliser la manipulation faisant varier l'espace libre. La simple connexion puis déconnexion suffit désormais ! 👍
Et encore mieux que cela, superbe amélioration de la
Graph Math+, il devient désormais possible de désactiver le mode examen par simple connexion à un hôte
USB passif, c'est-à-dire une simple connexion électrique sans le moindre besoin d'échange de données. On peut citer par exemple un chargeur
USB secteur ou encore une simple batterie
USB. Voici qui rend le mode examen de la
Graph Math+ le moins contraignant à désactiver pour les candidats en fin d'épreuve, félicitations
Casio ! 👍


L'application
Paramètres permet de configurer ta calculatrice. Elle n'est pas organisée en onglets mais se présente sous la forme d'un menu.
Réinitialisation par exemple permet d'effacer rapidement tout le contenu de la mémoire principale, de la mémoire de stockage, ou encore des deux à la fois.
Un des premiers réglages concerne la langue de l'interface de la calculatrice, avec 5 choix possibles :
- English pour l'Anglais
- Español pour l'Espagnol
- Français
- Italiano pour l'Italien
- Português pour le Portugais

C'est-à-dire que par rapport à la
Graph 90+E, nous perdons 2 langues :
- le Chinois qui sera peut-être développé et rajouté ultérieurement
- et de façon moins surprenante l'Allemand, l'Allemagne ayant fait en effet le choix surprenant d'interdire les calculatrices graphiques d'entrée et milieu de gamme à l'horizon de la session 2030 de l'Abitur, alors que paradoxalement les simples calculatrices scientifiques et calculatrices graphiques formelles haut de gamme restent autorisées, un grand écart nous étant difficilement compréhensible
Tu peux également configurer entre autres :
- le type de piles AAA utilisées (alcalines, ou rechargeables Ni-MH), très important à régler correctement pour la bonne détection de l'état des piles
- la luminosité du rétroéclairage
- les paramètres d'économie d'énergie : délais d'inactivité avant arrêt du rétroéclairage de l'écran puis extinction de la calculatrice
En France avec les énormes volumes de calculatrices graphiques en circulation chaque année, un gros problème est la perte ou le vol. Cela peut concerner aussi bien les élèves avec leur machine individuelle, que les enseignants disposant d'un stock de machines prêtées aux élèves.
Pour identifier ta calculatrice graphique
Casio, tu pouvais conserver une photo du numéro de série à code barre présent sur l'autocollant dans le compartiment des piles.
Sauf que cet autocollant pouvait être perdu, abîmé, ou volontairement retiré par un voleur.
La
Graph 90+E te permettait quelque chose d'un peu plus poussé qui aurait pu être génial, la signature électronique de ta calculatrice. Tu pouvais en effet y enregistrer en mémoire
Flash des noms d'utilisateur et organisation, informations montrées à chaque extinction de la calculatrice, et protéger leur modification par un mot de passe. Les informations étaient alors consultables dans l'application
Système et également rappelées sur l'écran du logo s'affichant à chaque extinction de la calculatrice.
A priori une belle protection contre la perte ou le vol... sauf que
Casio n'a pas osé aller jusqu'au bout.
Casio n'a pas voulu laisser tomber les utilisateurs oubliant leur mot de passe, ou acheteurs de calculatrices d'occasion à qui on ne communiquerait pas le mot de passe en question, et qui auraient alors été définitivement dans l'impossibilité de modifier les informations d'identification enregistrées.

Une combinaison permettait en effet d'effacer ce mot de passe et les données associées sur l'ensemble des
Graph 90+E :
- éteindre la calculatrice
- maintenir enfoncées les touches
F2
↑
- sans les relâcher, allumer la calculatrice en maintenant enfoncée la touche
AC/ON
(si tout a bien été fait, on obtient la fenêtre popup de réinitialisation) - taper non pas
F1
comme indiqué mais 9
pour confirmer la réinitialisation
Une combinaison publique sur Internet et cassant ainsi complètement la sécurité de la chose, car utilisable par n'importe quel voleur pour écraser immédiatement ta signature élecronique de ta calculatrice. Dans sa large bienveillance ne souhaitant abandonné personne sur le bord du chemin,
Casio avait ainsi rendu inefficace son propre outil de protection contre le vol.

Avec la
Graph Math+,
Casio change cela.
La signature électrique est conservée avec toujours un affichage à l'écran d'extinction de la calculatrice
(mais uniquement hors mode examen, car on pourrait bien y glisser une toute petite donnée utilisable).
Une idée de changement aurait été de conserver le mot de passe et supprimer la possibilité offerte à n'importe qui de le réinitialiser, mais ce n'est apparemment pas ce qui a été retenu.
Bien au contraire,
Casio a simplement supprimé le mot de passe ; c'est-à-dire que n'importe qui peut désormais changer librement la signature électronique de la calculatrice, rendant cette dernière désormais totalement inutile en tant qu'outil d'identification des machines.
En remplacement nouveauté,
Casio affiche désormais un numéro de série logiciel unique inaltérable à l'écran de configuration de la signature, et dont il te suffira de conserver une photo quelque part.

Si le passage à un connecteur
USB-C constitue matériellement une évolution majeure, toutefois logiciellement nous constatons à ce jour un recul important de la connectivité
USB de la
Graph Math+ par rapport à la
Graph 90+E.
Pour la connectivité
USB, plusieurs choix ne sont plus proposés dans la fenêtre
popup s'ouvrant lorsque l'on branche la calculatrice à un hôte USB. Il n'est en effet plus possible :
- d'effectuer une capture d'écran de la calculatrice directement depuis un ordinateur (via le logiciel Screen Receiver)
- de présenter en direct l'écran de la calculatrice par connexion à un ordinateur muni également du logiciel Screen Receiver
- de présenter en direct l'écran de la calculatrice par connexion à un vidéoprojecteur de marque Casio
Les enseignants pourront continuer à faire ce genre de chose, mais ils devront utiliser l'émulateur
Casio Graph Math+ à la place de la calculatrice physique.
C'est d'ailleurs dommage car même si l'émulateur permet beaucoup de choses dans un contexte académique, il ne permet pas de reproduire tous les menus de la calculatrice de façon complète ou identique, notamment tout ce qui est un petit peu plus technique et malgré tout parfois utile en classe. On peut par exemple citer des différences dans les menus des applications
Mémoire,
Mode Examen ou
Paramètres, ainsi qu'une impossibilité d'accéder au manu d'auto-diagnostic puisque l'émulateur ne permet pas de maintenir enfoncées plusieurs touches simultanément.
Ce recul est bien embêtant pour nous, car les captures d'écran nous servaient à illustrer rapidement et proprement divers tutoriels faisant appel à ces menus.
Les seuls et uniques usages restants pour la connectivité
USB semblent être uniquement, comme listés, le transfert de fichiers entre la calculatrice et un ordinateur, ainsi que la mise à jour du système d'exploitation de la calculatrice depuis un ordinateur.
Du côté de la connectivité série
(mini-Jack), la disparition des applications
Lien et
E-CON4 suggérait déjà qu'il n'était pour le moment plus possible de transférer directement des données entre 2 calculatrices, ou encore d'effectuer une acquisition de mesures physiques via une interface
CMA CLab.
Mais histoire de savoir si ces changements sont temporaires ou durables, nous avons testé des envois de donnée vers la
Graph Math+ depuis une autre calculatrice :
- si la Graph Math+ n'est pas en mode examen, aucune réaction et la calculatrice émettrice finit par indiquer une erreur de transmission après quelques secondes
- si la Graph Math+ est en mode examen, l'envoi se termine apparemment immédiatement sans que la machine émettrice n'indique d'erreur (bizarrement, même pour l'envoi d'un gros fichier), le mode examen de la Graph Math+ se désactive, mais les données soi-disant transférées avec succès ne sont pas rajoutées dans sa mémoire
Il semble donc que la
Graph Math+ soit toujours capable d'écouter ce qui arrive sur le port série, et d'être capable de le faire de façon permanente en tâche d'arrière plan
(plus besoin de basculer manuellement la machine en mode réception de données ce qui de toutes façons n'est plus réalisable sans l'application Lien/LINK)... mais malheureusement la
Graph Math+ ne fait ça qu'en mode examen et de plus ignore royalement le contenu des données en question.
Casio semble donc s'être donné la peine de désactiver/contourner des pans entiers du protocole de communication, ce qui semble indiquer que ce changement serait hélas sans retour.
Pour les transferts de données entre calculatrices, la suppression peut se comprendre :
- D'une part cette fonctionnalité historique a été introduite par Casio avec ses modèles de rentrée 1992, à une époque où les ordinateurs ne couraient pas les rues. C'est sans doute beaucoup moins utilisé de nos jours.
- Peut-être y a-t-il eu également des considérations par rapport au mode examen, dont les spécifications en France interdisent toute capacité de transfert de données une fois le mode examen activé. Si la capacité n'existe tout simplement plus, rien de particulier à coder, et aucune ambiguïté possible.
Nous comprenons mais regrettons malgré tout ce changement, le transfert de données entre calculatrices restant utile pour se partager rapidement de grosses données
(matrice, vecteur, liste) ou scripts Python dans une salle ou un couloir, sans avoir besoin de s'embêter à aller chercher, allumer et configurer un ordinateur.

Mais l'apparente désactivation de tout transfert de données implique aussi l'impossibilité d'effectuer une acquisition de mesures physiques via une interface
CMA CLab. C'est ici très surprenant que
Casio ait abandonné cette possibilité à l'intérêt scolaire pourtant certain, notamment pour les TPs de Physique-Chimie ou projets STEM. Nous avons deux hypothèses :
- l'interface CMA CLab est à notre connaissance, hélas, très peu vendue et utilisée, au moins pour la France, et Casio a pu faire le choix d'abandonner cette fonctionnalité car jugée ne pas servir à suffisamment de monde
- ou alors Casio a prévu une nouvelle interface se connectant cette fois-ci en USB lors d'une mise à jour future, mais c'est à prendre avec des pincettes car jusqu'ici les calculatrices Casio n'ont jamais supporté le mode hôte USB, c'est-à-dire la possibilité d'accueillir, reconnaître et gérer des périphériques USB
Nous préférerions ce dernier point plutôt qu'à un abandon pur et simple, mais c'est sans garantie.
Bref pour résumer, par élimination, le seul et unique usage restant pour la connectivité série sur
Graph Math+ semble être la désactivation du mode examen par connexion entre elles de 2 calculatrices.
À notre sens un coût non optimal d'avoir conservé un port
mini-Jack 2.5mm juste pour la désactivation du mode examen, mais peut-être que la développement du support d'un mode hôte
USB pour continuer à permettre la désactivation depuis une 2
e calculatrice n'était pas envisageable
(trop coûteux, techniquement complexe ou impossible à réaliser dans le temps de développement imparti).
Comme tu as pu voir plus haut, les câbles
USB et
mini-Jack ne sont plus fournis avec la calculatrice ; peut-être un moyen pour
Casio de faire un effort sur le prix en faveur des utilisateurs en cette période de forte inflation.
Il sera toutefois possible d'acquérir ces câbles séparément,
Casio ayant prévu la commercialisation d'un kit
SB-2000 comprenant un câble
USB-C et un câble
mini-Jack 2.5mm (SB-62).
Toutefois tu restes parfaitement libre d'utiliser des câbles non officiels en ta possession :
- pour l'USB-C ce n'est sans doute pas bien gênant, tu disposes probablement déjà de plusieurs câbles, mais attention juste aux câbles pas chers qui ne sont câblés que pour la charge et ne permettront pas le transfert de fichiers ni la future mise à jour majeure en 2025
- le câble mini-Jack 2.5mm te sera essentiel pour désactiver le mode examen, donc il va falloir te le procurer d'une façon ou d'une autre - de la connectique adéquate est encore trouvable en magasin aux rayons Hifi/Audio, où tu dois choisir de la connectique mini-Jack 2.5mm stéréo
Profitons-en pour connecter la calculatrice en
USB à un ordinateur, et explorer un peu ce qui se passe.
Appraît alors sur l'ordinateur un disque
USB reprenant le contenu de la mémoire de stockage. Le disque en question annonce
16,07 Mo de capacité, aussi bien avec la
Graph 90+E que la
Graph Math+.
Différence majeure toutefois :
- avec la Graph 90+E, le disque comporte une unique partition formatée en FAT16 et occupant toute la capacité du disque
- avec la Graph Math+, le disque est scindé en 2 partitions, dont une seule formatée cette fois-ci en FAT12 avec seulement 4,55 Mo de capacité, laissant donc en apparence une partition de 9,51 Mo non utilisée
C'est cohérent par rapport à la réduction de la capacité de mémoire de stockage vue plus haut sur
Graph Math+.
L'outil avec lequel nous avons testé ne voulait pas redimensionner la partition en question, mais il ne faut de toutes façons sûrement pas s'attendre à ce que cela soit aussi simple.
F3) Fichiers mémoire principale .g4m et compatibilité .g1m/g2m/g3m/txtGo to top Les données présentes en mémoire principale peuvent être exportées sous la forme de fichiers mémoire, et alors transférées sur ordinateur pour sauvegarde ou bien transfert vers une autre calculatrice. Ces fichiers peuvent contenir tous les types de données pouvant être stockées en mémoire principale
(entre autres matrices, vecteurs, listes, et sur les anciens modèles programmes).
On distingue différentes extensions pour les fichiers mémoire :
- .g1m et .g2m : calculatrices graphiques monochromes Graph 25+E/Pro, Graph 35+E, et Graph 75/85/95
- .g3m : calculatrices graphiques couleur Graph 90+E et fx-CG10/20/50
- et .g4m, spécifique à la Graph Math+
Nous avons regardé et le codage des données mémoire dans ces fichiers n'a pas changé avec la
Graph Math+. Les seules différences sont :
- l'extension qui passe à .g4m, mais qui est sans importance sur calculatrice
- de petites différences dans les 32 octets de header

Pour charger un fichier mémoire sur une
Graph Math+ connectée en
USB à un ordinateur, 2 possibilités :
- soit on copie le fichier mémoire dans le dossier /@MainMem/ de la calculatrice, et il sera automatiquement chargé à la déconnexion
- soit on copie le fichier hors de ce dossier, il sera alors accessible en mémoire de stockage et pourra être chargé manuellement en mémoire principale avec le menu contextuel
...
, à la différence plusieurs fois si nécessaire
À première vue pas de rétrocompatibilité, la
Graph Math+ n'accepte pas de charger les fichiers
.g1m,
.g2m ou
.g3m générés sur d'anciens modèles, et bien évidemment, changer l'extension à
.g4m ne suffit pas à les faire passer, à cause des différences de
header, la
Graph Math+ retournant une erreur :
- Echecconversion données (sic, avec un oubli d'espacement) si on passe par le dossier /@MainMem/
- "Invalid Type" pour un chargement manuel à partir de la mémoire de stockage

Toutefois, si on corrige un simple octet dans le
header pour le faire ressembler à celui des fichiers générés sur
Graph Math+ (à l'offset 0x08, type de fichier à régler sur la valeur générique 0x31 justement utilisée par certains logiciels d'édition), alors ça passe.
Si si regarde, ça marche parfaitement, nous avons même réussi à faire passer un programme
Casio Basic, la
Graph Math+ ayant même toute seule créé le dossier
PROGRAM en mémoire principale pour le mettre dedans, même si malheureusement nous n'avons hélas rien pour l'ouvrir et le lancer :
Il semble donc que le support des programmes
Casio Basic n'ait pas été retiré du code du protocole. Peut-être que l'application
Programmes sera à la différence toujours présente sur les modèles équivalents hors de France dont la
fx-CG100.
Il y avait également une autre méthode pour charger des programmes sur les anciens modèles, il suffisait de mettre le code source en clair dans un fichier texte
.txt et de copier ce dernier soit dans le dossier
/@MainMem/PROGRAM/, soit en dehors en mémoire de stockage pour un chargement ultérieur.
Cette façon de faire par contre semble bien avoir été désactivée sur
Graph Math+, nous obtenons les messages d'erreur précédents dans les deux cas.
F4) Fichiers images .g4p et compatibilité .g3p/g3b/bmpGo to top Comme clairement indiqué au clavier, la combinaison
SHIFT
×10ˣ
permet de prendre une capture de l'écran de la
Graph Math+, tout comme on pouvait déjà le faire sur
Graph 90+ELes captures d'écran sont alors enregistrée dans le dossier
\Capt de la mémoire de stockage. Mais là où la
Graph 90+E enregistrait par défaut dans un format d'image
.g3p spécifique à
Casio, la
Graph Math+ utilise par défaut un format
.g4p qu'il va nous falloir creuser.
Dans l'application
Mémoire, à partir d'un fichier sélectionné en mémoire de stockage, le menu contextuel
...
permet via son entrée
Détails d'obtenir un écran avec :
- nom du fichier
- type du fichier si l'extension est reconnue
- taille du fichier
- dimensions si il s'agit d'un fichier image gérée (et nous remarquons vite que les captures d'écran sont prises en 384×216 pixels, c'est-à-dire avec la barre de statut en haut d'écran)
- et enfin dans le cas d'une image gérée, son affichage en arrière plan (que l'on peut faire passer au premier plan en masquant les informations précédentes à l'aide des flèches horizontales)
De suite, petit exemple illustrant tout ceci avec une capture de l'écran d'accueil :
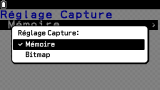
Par défaut donc, la
Graph Math+ enregistre les captures d'écran au format
.g4p. Mais tu peux aussi dans l'application
Paramètres choisir d'enregistrer au format
Bitmap (.bmp).
Mais dans le cas d'une image
.bmp, bien que le type de fichier soit parfaitement reconnu, aucun aperçu de l'image ne sera affichable sur calculatrice :
C'est que les 2 formats d'images visent des objectifs distincts :
- pour le format .g4p, l'utilisation sur calculatrice
- pour le format .bmp, l'utilisation sur ordinateur
La
Graph 90+E utilisait donc à la place un format
.g3p.
Testons de suite ce que ça donne sur
Graph Math+, avec la collection d'exemples d'images
.g3p qui étaient préchargées en usine dans la
Graph 90+E.
Et bien visiblement ça marche, la
Graph Math+ reconnaît parfaitement les images
.g3p et les gère apparemment en lecture aussi bien que les
.g4p :
Inversement par contre, les images
.g4p ne seront pas exploitables sur
Graph 90+E, même après renommage pour passer l'extension du nom de fichier en
.g3p, la machine signalant une erreur de données.
À y regarder de plus près, les formats d'image
.g3p et
.g4p semblent pourtant identiques au niveau du codage des données.
En fait, en plus de l'extension de fichier, tout ce qui change c'est une simple signature en en-tête :
- CP0100Ly755 pour la format .g3p (LY755 étant la référence du modèle fx-CG20 ayant précédé la Graph 90+E)
- CP0100Cy875 pour le format .g4p, (CY875 étant la référence de la Graph Math+)
Nous ignorons pourquoi soudainement après 12 ans de modèles utilisant ce format d'écran couleur et le même format d'images
.g3p,
Casio a éprouvé le besoin de distinguer les images produites par ou pour la
Graph Math+, en passant au format
.g4p incompatible avec les modèles précédents.
Un autre format d'image était également géré par la
Graph 90+E, le
.g3b pour les images animées, exploitables via l'application
Plot Image.
Rappelons que cette application est absente de la
Graph Math+, et que contrairement à d'autres sont retour n'a pas été annoncé pour la mise à jour majeure V2 de 2025.
Et bien il est possible qu'il ne soit tout simplement pas prévu de reprendre cette application sur
Graph Math+. En effet, nous nous rendons rapidement compte à l'aide de l'application
Mémoire de la
Graph Math+, que les exemples d'images
.g3b préchargées sur
Graph 90+E :
- n'ont pas d'aperçu affiché en arrière plan
- n'ont pas leurs dimensions affichées
- ne sont même pas reconnues en tant qu'images, le type restant à Inconnu
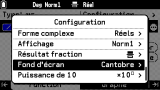
Si l'usage du format
.bmp a été évoqué, à quoi servent les images
.g3p et
.g4p sur
Graph Math+ ?
Et bien le menu
SETTINGS
te permet de choisir une image à mettre en fond d'écran de la vue graphique, pour des activités destinées à montrer que les mathématiques nous entourent
(où trouve-t-on des paraboles, etc.)
F5) Point sur les applications et langues additionnellesGo to top La
Graph 90+E était une machine librement extensible, même si les capacités rajoutées n'étaient utilisables que hors mode examen.
Il était possible de lui installer :
- en plus des languges intégrées, des langues additionnelles, comme le Russe (fichiers .g3l)
- en plus des applications intégrées, des applications additionnelles (fichiers .g3a), que des développeurs tiers pouvaient librement créer en compilant leur code source écrit en langage C à l'aide du SDK
On compte pléthore de pépites qu'il serait trop long de toutes couvrir dans ce test. Citons (trop) rapidement :
Et bien selon nos tests, la Graph Math+ perd cette modularité.
Les fichiers .g3l et .g3a ne sont plus supportés. Il n'est plus possible de se rajouter librement des fonctionnalités (langues ou applications) en fonction de ses besoins ou envies, du moins dans la version actuelle de la calculatrice.
Nous n'interdisons à personne d'espérer un retour des applications additionnelles communautaires dans une mise à jour future, mais pour le moment cette fonctionnalité contrairement à bien d'autres n'a pas été annoncée pour la mise à jour majeure de 2025.
Nous t'avouerons qu'après la volonté très forte que nous avons vue un peu plus haut d'alléger/simplifier le système d'exploitation en supprimant nombre de possibilités jugées désuètes ou non académiques, nous n'avons à ce jour pas grand espoir... Mais nous serions les premiers heureux de nous tromper.
G1) Moteur de calcul en virgule flottanteGo to top Continuons à explorer ce que renferme la
Graph Math+, en creusant maintenant son moteur de calcul numérique. Il s'agit du moteur utilisé par toutes les applications pour évaluer les saisies en écriture décimale, à l'exception de l'application
Python.
Les calculatrices utilisent pour cela un moteur de calcul dit en virgule flottante. Dans ce type de moteur, les nombres sont codés sous la forme suivante :
$mathjax$M\times 10^E$mathjax$
avec
M la mantisse et
E l'exposant.
Chaque implémentation d'un moteur de calcul en virgule flottante, se caractérise par le codage utilisé pour la mantisse et l'exposant, et donc les limites en découlant.
Commençons par déterminer les plus petites et plus grandes valeurs autorisées pour l'exposant. Pour cela, il nous suffit de simuler pas à pas à l'écran de calcul le fonctionnement des 2 scripts
Python suivants.

- Code: Select all
def expmin():
a, e = 1., 0
while a > 0:
a /= 10
e += 1
return -e
À force de divisions par 10, nous finissons par obtenir l'affichage d'un résultat nul. Le dernier résultat non nul utilisait l'exposant minimal autorisé :
-99.
- Code: Select all
def expmax():
a, e = 1., 0
while True:
try:
a *= 10
e += 1
except: break
return e
À force ici de multiplications par 10, nous finissons par déclencher une exception de dépassement de capacité. Le dernier résultat avant erreur utilisait l'exposant maximal autorisé :
+99.
La
Graph Math+ code donc en interne les nombres avec des exposants allant de
-99 à
+99, comme la
Graph 90+E, mais aussi comme beaucoup de calculatrices graphiques de milieu de gamme, donc rien de véritablement surprenant pour le moment.
Passons donc à la mantisse et effectuons un test de précision afin d'estimer la taille utilisée par le codage.
Voici ici encore la transcription en
Python des saisies que nous allons enchaîner à l'écran de calcul :
- Code: Select all
def precm(b):
k, b = 0, float(b)
while 1 + b**-k-1 > 0:
k += 1
return k


Commençons en base décimale, ce qui correspondrait à l'appel
precm(10).
Si
$mathjax$1+10^{-12}-1$mathjax$
renvoie certes un résultat correct,
$mathjax$1+10^{-13}-1$mathjax$
renvoie pour sa part un résultat nul.
Le codage des mantisses supporte donc au maximum 13 chiffres significatifs en base décimale.
Poursuivons en base binaire, ce qui correspondrait à l'appel
precm(2).
Si
$mathjax$1+2^{-39}-1$mathjax$
renvoie encore un résultat correct,
$mathjax$1+2^{-40}-1$mathjax$
renvoie quant à lui un résultat nul.
Le codage des mantisses supporte donc au maximum 40 bits significatifs.
Cela correspond très exactement aux mêmes paramètres de codage utilisés par la
Graph 90+E.
Mais allons plus loin avant de faire des conclusions hatives, car nous avons un moyen d'identifier le moteur de calcul.
Chez les passionnés de calculatrices, il y avait dans le temps un test permettant d'identifier les microprocesseurs utilisés, celui de la signature trigonométrique.
Prenons en mode degrés le calcul suivant :
$mathjax$Arcsin\left(Arccos\left(Arctan\left(tan\left(cos\left(sin\left(9\right)\right)\right)\right)\right)\right)$mathjax$
Le résultat théorique est de 9, mais en pratique les moteurs de calcul en virgule flottante de nos calculatrices répondent une valeur approchante, que nous appellerons justement signature trigonométrique. En classant alors les calculatrices par signature, l'on prétendait regrouper les calculatrices utilisant le même processeur, ou du moins les calculatrices utilisant des processeurs partageant un même cœur de calcul.
En réalité ce n'est pas exact, ce test permet de regrouper les calculatrices utilisant le même moteur de calcul, et ce peu importe qu'il soit matériel ou logiciel.
Dans le temps, alors que les calculatrices étaient fort limitées en capacité mémoire, les moteurs de calcul étaient écrits en langage assembleur
(langage collant au fonctionnement interne de chaque processeur) puis assemblés en langage machine. Afin d'économiser de la mémoire, plutôt que de les recoder ces moteurs exploitaient au maximum les fonctions de calcul déjà intégrées au processeur. La signature trigonométrique était donc fortement dépendante du processeur et de son cœur de calcul.
De nos jours la mémoire n'est plus un problème, et il n'est pas rare d'avoir des moteurs de calcul entièrement logiciels, écrits intégralement dans un langage de plus haut niveau puis compilés en langage machine. Dans ce cas il est même possible que des calculatrices utilisant des processeurs complètement différents partagent malgré tout la même signature trigonométrique.
Ceci étant dit, la signature trigonométrique de la
Graph Math+ est de
8.99999999759468, soit très exactement la même que sur
Graph 90+E.
Même moteur de calcul donc, ce qui ne prouve certes pas encore que l'on reste sur un processeur de la même famille, mais c'est une hypothèse à envisager très sérieusement désormais, et nous allons faire tout ce qu'il faut pour pouvoir la confirmer ou l'infirmer.
Sur
Graph 90+E, il était possible via une combinaison secrète d'accéder à un menu d'auto-diagnostic permettant d'en apprendre davantage sur le fonctionnement internet de la calculatrice.
Il fallait pour cela :
- éteindre la calculatrice
- maintenir enfoncées les touches
OPTN
×10ˣ
- sans les relâcher, allumer la calculatrice en maintenant enfoncée la touche
AC/ON
(si tout a bien été fait, on obtient la fenêtre popup d'accès) - relâcher toutes les touches
- taper
F1
pour valider l'accès - taper comme indiqué
9
pour confirmer l'accès
Problème, la plupart de ces touches n'existent plus sur
Graph Math+...


Pour accéder au menu d'auto-diagnostic sur
Graph Math+, il nous faut trouver par quelles touches
Casio a remplacé les précédentes.
Nous avons une bonne nouvelle, à force de tentatives nous avons réussi. Pour accéder au menu d'auto-diagnostic caché de la
Graph Math+, il te faut :
- éteindre la calculatrice
- maintenir enfoncées les touches
HOME
×10ˣ
AC
- sans les relâcher, allumer la calculatrice en maintenant enfoncée la touche
ON
(si tout a bien été fait, on obtient la fenêtre popup d'accès) - relâcher toutes les touches
- taper
SETTINGS
pour valider l'accès - taper comme indiqué
9
pour confirmer l'accès

C'est donc parti pour un peu d'exploration.
Le menu d'accueil nous confirme en en-tête la référence du logiciel déjà remarquée plus haut,
CY875.
Il nous rajoute également les valeurs des drapeaux
Qbits,
011 exactement comme sur
Graph 90+E. Ces drapeaux sont liés aux positions de 3 résistances à proximité du processeur. Avec 2 emplacements possibles pour chacune, elles permettent d'adapter le comportement de la calculatrice. L'une d'entre elles par exemple indique la présence d'une diode examen, avec des différences sur l'économie d'énergie lorsque l'on éteint la calculatrice en mode examen.


L'entrée
VERSION nous permet d'en apprendre d'avantage sur le système d'exploitation :
- l'écran obtenu nous rappelle le numéro de version du système vu plus haut, 01.00.2202
- mais nous indique en plus sa date de compilation, ligne DateO avec 2024.0209.1158 pour le 9 Février 2024 à 11h58
De plus, la ligne
DateA nous précise la date du compilation du
Boot code (code de démarrage), ici
2017.0106.2008 pour il y a fort fort longtemps le
6 janvier 2017 à
20h08... exactement comme le
Boot code de la
Graph 90+E !
Le
Boot code de la
Graph 90+E semble donc avoir été réutilisé à l'identique pour la
Graph Math+. L'absence du besoin de recompiler quelque chose d'aussi sensible et lité au matériel que le
Boot Code, implique plusieurs choses d'importance qu'il nous faudra confirmer :
- le matériel Graph Math+ est donc très probablement similaire à celui de la Graph 90+E
- une certaine compatibilité entre les Graph 90+E et Graph Math+ au niveau du code machine, ce qui concerne aussi bien le système d'exploitation que les applications additionnelles...
- en effet excellente nouvelle suite à ce choix, en théorie, les applications additionnelles Graph 90+E devraient pouvoir fonctionner sans la moindre modification sur Graph Math+, si Casio veut bien nous faire le plaisir de réactiver cette fonctionnalité ! 👍

L'entrée
TEST permet entre autres de tester les mémoires
RAM et
ROM, mais hélas ne révèle rien sur leurs capacités :


Nous y trouvons aussi de quoi tester l'écran LCD. Plusieurs mires
(motifs de test) y sont disponibles, dont un dégradé permettant de confirmer le fonctionnement de l'écran en couleurs
RGB-565 comme vu plus haut.
Régal pour les yeux illustrant les capacités de ce très bel écran, on trouve dans les réglages du test une entrée
Sample Picture (échantillon d'image).
On y retrouve alors l'image de forêt enneigée qui était déjà présente sur
Graph 90+E, mais également de nouvelles images rajoutées depuis :
Il existait un autre menu caché sur
Graph 90+E, accessible via une combinaison similaire et offant d'autres possibilités d'exploration.
Pour y accéder il fallait :
- éteindre la calculatrice
- maintenir enfoncées les touches
OPTN
×10ˣ
- sans les relâcher, allumer la calculatrice en maintenant enfoncée la touche
AC/ON
(si tout a bien été fait, on obtient la fenêtre popup d'accès) - relâcher toutes les touches
- taper
5
9
6
3
pour valider l'accès


On traduit cette fois-ci beaucoup plus aisément la combinaison de touches pour
Graph Math+ :
- éteindre la calculatrice
- maintenir enfoncées les touches
HOME
×10ˣ
AC
- sans les relâcher, allumer la calculatrice en maintenant enfoncée la touche
ON
(si tout a bien été fait, on obtient la fenêtre popup d'accès) - relâcher toutes les touches
- taper
5
9
6
3
pour valider l'accès

Dans l'entrée
Font/Lang Check, on trouve par exemple un accès complet à la table des caractères de la calculatrice.
Comme tu peux voir, c'est hautement plus riche et complet que ce qui est utilisable et affichabe en
Python, c'est bien dommage de ne pas pouvoir les exploiter dans nos scripts :


Nous pouvons maintenant aller voir dans l'entrée
File System puis
FugueInfo.
La sous-entrée
Volume Info nous permet d'avoir des informations sur la partition correspondant à la mémoire de stockage, confirmant la réduction à exactement
4,739 Mo de capacité, ainsi que le passage au système de fichier
FAT12 :


Revenons à l'accueil du menu de test, et notre attention est attirée par une nouvelle entrée
etc qui n'était pas présente sur
Graph 90+E. Nous y trouvons entre autres de quoi activer enfin la communication avec le logiciel
Screen Receiver ! 👍
Le menu test, inaccessible sur émulateur, nous est donc enfin présenté en direct sur ordinateur avec la possibilité d'en prendre des captures d'écran propres :
Et encore mieux que ça, le lien avec le logiciel
Screen Receiver reste actif tant que la calculatrice ne redémarre pas, et tant qu'elle ne reste pas éteinte trop longtemps.
Nous pouvons donc quitter le menu de test et obtenir enfin des captures d'autres écrans inaccessibles sur émulateur
(mode examen, menu d'auto-diagnostic, etc.) :
Profitons-en d'ailleurs pour te récupérer les échantillons d'images du menu d'auto-diagnostic : 😉
C'est bien que ça reste donc possible, mais les manipulations permettant d'activer ce mode restent assez lourdes, et il faut de plus faire attention à ce que la calculatrice ne redémarre pas et reste allumée afin de ne pas avoir en prime à les refaire.

Bon… nombre d'indices précédents nous ont pointé vers une forte similarité matérielle entre la
Graph Math+ et la
Graph 90+E. Mais similarité ne signifie pas forcément matériel identique.
Il est enfin grand temps de regarder ce que la
Graph Math+ a dans le ventre.
Le matériel s'articule en 2 cartes électroniques reliées par une nappe flexible:
- la carte avec comme visible l'alimentation par piles et au dos la matrice du clavier, de référence PWB-CY875-E4
- et la carte mère avec tout le reste, sans référence visible de ce côté
Puisque nous avons de quoi, on peut même comparer les cartes
Graph Math+ avec celles du prototype testé chez
Casio :
Les seules différences visibles semblent ne concerner que les timbres à date.
Pour la carte d'alimentation, nous avons :
- 2345 (production de la carte la 45e semaine de 2023) sur le prototype Graph Math+ (novembre 2023)
- 2352 (production de la carte la 52e semaine de 2023) sur la Graph Math+ finale (décembre 2023)
Pour la carte mère, nous avons :
- 5023 (production de la carte la 50e semaine de 2023) sur le prototype Graph Math+ (décembre 2023)
- 0324 (production de la carte la 3e semaine de 2024) sur la Graph Math+ finale (janvier 2024)
Comparons maintenant les cartes
Graph 90+E et
Graph Math+ :
Déjà un bon point, là où la nappe flexible reliant les 2 cartes était soudée sur
Graph 90+E, elle est amovible sur
Graph Math+. Un bon point pour la réparabilité ! 👍
Passons maintenant aux cartes mère. Les positions des port
USB et
mini-Jack étant inversées, comme on pouvait s'y attendre nombre de composants changent de position, passant d'un côté à un autre, mais pas tous. Les cartes ne sont donc ici pas comparables par superposition, toutefois leur articulation autour des différents composantes principaux semble être extrêmement similaire.
Les cartes mère
Graph 90+E et
Graph Math+ font appel à 3 composants majeurs :
- la puce RAM, dans les deux cas une M12L64164A de chez ESMT, offrant 8 Mio de mémoire SDRAM
- la puce ROM, dans les deux cas une S99-50272 de chez Spansion, offrant 32 Mio de mémoire Flash
- le processeur, sans référence lisible
Casio ne semble donc pas avoir profité de l'occasion de la sortie de la
Graph Math+ pour faire évoluer les capacités mémoire par rapport à la
Graph 90+E de rentrée 2017.
Et niveau performances, que donne la
Graph Math+ ?
Reprenons les applications précédentes pour répondre. Pour une réponse indiscutable, nous te proposons de faire le tour de la question en pas moins de 4 tests auxquels nous soumettons justement chaque nouvelle calculatrice compatible :
- calcul
- graphique
- flottants Python
- entiers Python
Commençons par un test de performances via un calcul. Pour les modèles disposant de l'opérateur de sommation
(Σ), nous retenons le calcul développé par
pier4r sur HP Museum, à évaluer en mode degrés :
$mathjax$\sum\limits_{x=1}^{1000}{\sqrt[3]{e^{sin\left(Arctan\left(x\right)\right)}}}$mathjax$
La
Graph Math+ sort la réponse en
8,56s.
- 0,475s : HP Prime G2
- 0,252s : NumWorks N0120
- 0,997s : TI-Nspire CX II
- 1,100s : NumWorks N0115
- 8,550s : Casio Graph 90+E
- 8,560s : Casio Graph Math+
- 13,800s : TI-82 Advanced Edition Python
- 14,100s : Casio Graph 35+E II, TI-83 Premium CE Edition Python
Passons maintenant à un test graphique, avec l'avantage d'être réalisable sur n'importe quelle calculatrice graphique.
À l'aide de la fonction auxiliaire d'expression
$mathjax$t(x)=\arcsin\left(\arccos\left(\arctan\left(\tan\left(\cos\left(\sin(x)\right)\right)\right)\right)\right)$mathjax$
, nous allons représenter graphiquement les 2 fonctions d'expressions suivantes :
$mathjax$f(x)=\arcsin\left(\arccos\left(\cos\left(\sin\left(t^2(x)\right)\right)\right)\right)$mathjax$
$mathjax$g(x)=-\arcsin\left(\arccos\left(\cos\left(\sin\left(t^2(x)\right)\right)\right)\right)$mathjax$
La
Graph Math+ donc, nous termine les deux représentations graphiques en
6,91s. Comme la fenêtre graphique utilise comme nous avons vu
379 colonnes, cela nous donne ici
18,2ms par colonne.
- 0,475ms/colonne : HP Prime G2
- 1,710 ms/colonne : NumWorks N0120
- 5,390 ms/colonne : NumWorks N0115
- 16,800 ms/colonne : Casio Graph 90+E
- 18,200 ms/colonne : Graph Math+
- 18,400 ms/colonne : TI-Nspire CX II
- 89,800 ms/colonne : Casio Graph 35+E II
- 170,000 ms/colonne : TI-82 Advanced Edition Python, TI-83 Premium CE Edition Python
Passons maintenant aux tests de performances concernant les calculatrices programmables en
Python.
Commençons par un calcul en virgule flottante. Voici la transcription en
Python d'un algorithme de seuil sur une suite numérique, niveau Première :
- Code: Select all
def seuil(d):
n = 0
u = 2.
d = d ** 2
while (u-1)**2 >= d:
u = 1 + 1/((1 - u)*(n + 1))
n = n + 1
return [n, u]
La
Graph Math+ met
3,57s à évaluer l'appel
seuil(0.008).
- 0,087s : HP Prime G2
- 0,201s : NumWorks N0120
- 0,297s : TI-Nspire CX II-T
- 0,714s : NumWorks N0115
- 3,270s : Graph 90+E
- 3,570s : Graph Math+
- 3,990s : TI-83 Premium CE Edition Python
- 4,010s : TI-82 Advanced Edition Python
- 9,21s : Graph 35+E II
Et terminons maintenant à un calcul
Python sur des entiers.
Voici donc un test de primalité retranscrit en
Python :
- Code: Select all
def nodivisorin(n, l):
for k in l:
if n // k * k == n:
return False
return True
def isprimep(n):
l, k = [3], 7
if n == 2 or n == 5: return True
if int(n) != n or n // 2 * 2 == n or n // 5 * 5 == 5:
return False
if n < k: return n in l
while k * k < n:
if nodivisorin(k,l): l.append(k)
k += 2 + 2*((k + 2) // 5 * 5 == k + 2)
r = nodivisorin(n, l)
return r
La
Graph Math+ met
1,53s à évaluer l'appel
isprimep(10000019).
- 0,171s : HP Prime G2
- 0,406s : NumWorks N0115
- 0,451s : TI-Nspire CX II-T
- 0,745s : NumWorks N0120
- 1,530s : Graph Math+
- 1,580s : Graph 90+E
- 4,39s : Graph 35+E II
- 8,910s : TI-83 Premium CE Edition Python
- 9,220s : TI-82 Advanced Edition Python
Comme bilan, comparons la
Graph Math+ à son illustre prédécesseur, la
Graph 90+E :
test | Graph 90+E | Graph Math+ |
calcul | 8,55s | 8,56s |
graphes | 16,8 ms/colonne | 18,2 ms/colonne |
flottants Python | 3,27s | 3,57s |
entiers Python | 1,58s | 1,53s |
Dans tous les cas les durées sont extrêmement proches, si bien qu'à l'imprécision des mesures près on peut les considérer comme identiques.
Le matériel
Graph Math+ de rentrée 2024 nous apparaît donc de plus en plus similaire
(si ce n'est identique) au matériel
Graph 90+E de rentrée 2017.
Compatibilité au niveau du code machine et maintenant performances identique, il s'agit donc non seulement d'un processeur 32 bits
Renesas SH4, mais très probablement également du même processeur que dans la
Graph 90+E de rentrée 2017, le
SH7305 toujours cadencé à
117,96 MHz.
Avec la
Graph Math+,
Casio semble donc s'être concentré sur l'amélioration du logiciel, et n'avoir pas du tout profité de l'occasion pour rafraîchir la plateforme matérielle malgré ses déjà 7 ans d'âge.
En conclusion, la Graph Math+ constitue une évolution majeure de la calculatrice graphique couleur par Casio.
Mais avec certains choix effectués, c'est un modèle qui va être très clivant.
Certains vont l'adorer pour certains points et d'autres tout au contraire la détester pour d'autres points, particulièrement parmi les anciens utilisateurs et fans de calculatrices Casio.
D'un côté, dans le contexte scolaire et donc essentiellement de nouveaux utilisateurs, la
Graph Math+ est un véritable petit bijou ! 😍
Casio nous offre une toute nouvelle interface, que nous pouvons caractériser en 3 points essentiels :
- Articulation de chaque application en onglets, qui permettent selon le contexte :
- soit de basculer entre différentes représentations des mêmes objets mathématiques, faisant travailler naturellement aux élèves la compétence représenter 👍
- soit de présenter les étapes successives à suivre dans la résolution 👍
- Navigation au sein de chaque onglet entièrement intuitive car s'appuyant en effet sur les touches fléchées du clavier. 👍
- Cherche à laisser le contexte d'appel visible autant que possible (fenêtres popup, astuces d'aide en ligne superposées à la barre de statut en haut d'écran, outils de sélection de caractères superposé sur la barre d'onglets en bas d'écran, ...) ce qui éviter de couper brutalement l'élève de son contexte. 👍
Mais
Casio est loin de s'être contenté de simplement refondre l'interface, le constructeur lui adjoint également un tout nouveau clavier conçu sur mesures ! 👍
Tout a été pensé pour le confort de tes petits doigts. On peut citer :
- afin de minimiser la distance parcourue par tes doigts, les 2 touches de validation pour un accès immédiat :
OK
lorsque les doigts seront autour du pavé directionnel en train de naviguer dans des menusEXE
lorsque les doigts seront sur la pavé numérique en train de saisir un calcul
- et, pour éviter un trop grand nombre d'appuis répétés sur les touches fléchées, élément indispensable pour toute interface par onglets faisant un usage intensif des touches fléchées, 4 touches fléchées supplémentaires :
- 2 pour passer à l'onglet précédent ou suivant d'une simple pression de touche, sans chemin compliqué à parcourir à l'écran !
- et 2 pour défiler l'affichage d'une hauteur d'écran vers le haut ou vers le bas, ici encore d'une seule pression de touche !
Rajoutons nombre d'éléments inventés pour une meilleure compréhension et une utilisation plus efficiente en classe, entre autres :
- rappel de la configuration de la fenêtre graphique avant affichage
- démarrage de l'application Python sur un script, évitant tout passage technique par un gestionnaire de fichiers/dossiers
- tous les éléments de définition d'une suite numérique présentés sur un même écran
La
Graph Math+ est ainsi un véritabe trésor, à la fois sur le plan de l'intuitivité, de l'ergonomie et de la pédagogie ! 😍
Cette capacité à exceller sur ces 3 axes fait de la
Graph Math+ une machine absolument remarquable ! 👍
Accessoirement, rappelons en
Python la tant attendue nouvelle fonction
getkey(), qui plus est non bloquante pour une interaction optimale avec l'utilisateur, nous ouvrant en grand les possibilités de développement
Python. Rappelons à ce sujet que nous apprécierions beaucoup avec ceci l'ajout d'une fonction
fill_rect() afin de pouvoir également optimiser les tracés graphiques.
La calculatrice est visiblement issue d'une longue et profonde réflexion, faisant la synthèse d'années de retours de la part d'utilisateurs et enseignants. Nous ne pouvons que nous incliner devant les hautes compétences des professeurs agrégés ayant contribué à la création de ce nouveau modèle :
- Djelloul Hidra, professeur agrégé de Mathématiques (académie de Nantes), et justement également consultant formateur pour CASIO France depuis bientôt 12 ans
- Thomas Lechenne, professeur agrégé de Mathématiques (académie de Besançon), et également consultant pour CASIO France depuis 16 ans
- Yves Coudert, professeur agrégé de Mathématiques s'occupant également de la spécialité NSI au Lycée Le Bon Sauveur à Le Vésinet (académie de Versailles), et également consultant pour CASIO France depuis 15 ans et demi
Merci à vous, vous avez conçu et de très loin la meilleure calculatrice graphique couleur de ces 5 dernières années ! ❤️
Casio Graph Math+, la calculatrice qui donne du sens aux Mathématiques ! 🎉
D'un autre point de vue, la
Graph Math+ souffre à ce jour d'un déficit en fonctionnalités.
Il manque plusieurs choses nous semblant essentielles pour un cursus scientifique au lycée :
- feuille de calcul / tableur
- tableau périodique des éléments
- bibliothèque de constantes physiques
De façon plus accessoire citons les graphes 3D, les animations de graphes paramétrés, la géométrie dynamique ou encore la simulation d'expériences aléatoires, des fonctionnalités qui étaient toutes présentes sur
Graph 90+E sous la forme d'applications.
Nous supposons que
Casio a manqué de temps, ces applications ayant été conçues pour l'ancien clavier
Graph 90+E et ayant donc en effet besoin d'être repensées pour épouser l'esprit de la nouvelle interface par onglets ainsi que sa navigation par touches fléchées.
Des fonctionnalités qui seront donc rajoutables à la
Graph Math+ lors de la publication de la mise à jour V2 majeure au premier semestre 2025.
La
Graph Math+ nous semble ainsi être un excellent choix pour un élève passant en Seconde pour cette rentrée 2024, élève qui pourra dès cette année faire évoluer gratuitement les capacités de la calculatrice avec ses besoins ! 👍
Nous serions à ce jour plus mesurés pour un élève plus avancé dans un cursus scientifique au lycée, passant en Première ou Terminale pour cette rentrée 2024. Mais ce problème sera donc réglé d'ici la rentrée 2025.
Et enfin, on touche à ce qui blesse, du moins parmi les anciens utilisateurs particulièrement fans du modèle précédent
Graph 90+E.
Pour satisfaire la demande légitime des utilisateurs moyens et enseignants d'avoir avec la
Graph Math+ une calculatrice plus simple à utiliser,
Casio n'a pas joué que sur l'intuitivité et l'ergonomie.
Casio a également cru bon de supprimer plein de fonctionnalités jugées désuètes ou inutiles
(car non académiques par exemple).
Et nous pouvons dire que
Casio n'a pas fait les choses à moitié, c'est une véritable purge. Nombre de fonctionnalités historiques caractéristiques de l'ADN des calculatrices graphiques
Casio disparaissent.
Parmi les choses qui disparaissent et pour lesquelles à la différence aucun retour n'a été annoncé, voici ce que nous retenons, par ordre d'importance.
Déjà, même si cela ne concerne que nous, nous avons la fort douloureuse disparition des captures instantanées d'écran de la calculatrice depuis un ordinateur avec
Screen Receiver qui nous embête pour la rédaction et l'illustration de tutoriels techniques... et nous a particulièrement bien embêtés dans le cadre de ce test, multipliant les manipulations à effectuer pour tout écran étant inaccessible ou bien non reproduit à l'identique sur émulateur.
Rajoutons la suppression de l'application
e-Activités, qui permettait la rédaction de documents scientifiques interactifs et dynamiques, incluant en effet des objets connectés avec les diverses applications scientifiques de la calculatrice
(saisies, calculs à évaluer, graphiques, diagrammes, etc). Sa suppression est compréhensible dans le sens où la plupart des utilisateurs ne s'en servaient que comme éditeur et lecteur de pompes. Mais elle bénéficiait malgré tout de son lot de fans en faisant un usage parfaitement légitime.
Nous arrivons maintenant aux 2 points les plus douloureux, car touchant à des fonctionnalités constituant le ciment de la communauté des utilisateurs de calculatrices
Casio.
Nous avons la suppression des programmes en langage
Casio Basic. Si on s'en tient à une lecture purement académique ça se comprend, en France les lycéens et lycéennes ne sont censés programmer qu'en
Python sur leur calculatrice.
Sauf que nous avons pour notre part également la chance d'avoir un point de vue extérieur ; pour des raisons que nous ignorons, le
Python sur calculatrice, ça ne marche pas, ou du moins pas aussi bien que le
Basic.
Le constat se résume en 2 points :
- même aujourd'hui en 2024, nous avons encore sur TI-Planet et Planète Casio, des jeunes nous partageant leurs petits jeux simplistes créés en langage TI-Basic ou Casio Basic, une activité créative à la fois ludique et formatrice
- nous n'avons quasiment personne (mis à part nous ou quelques très rares enseignants) partageant pour calculatrices ne serait-ce que le même genre de petits jeux en Python
Nous n'avons pas tous les éléments pour l'expliquer, mais nous avons plusieurs hypothèses :
- par rapport au Basic, une marche d'entrée beaucoup plus haute pour les élèves en Python avec la logique fonctionnelle à appréhender, faisant donc qu'il y a moins d'élèves codant en Python que ceux qui codent/codaient en Basic
- peut-être l'enseignement de la programmation par blocs orientée tracés au Collège, qui au lieu de la rendre plus naturelle nuirait à la transition vers le Python en Seconde
- un nombre encore trop important d'enseignants de Mathématiques ou Physique-Chimie n'abordant pas ou alors bien trop peu le Python (qui officiellement devrait être invoqué de façon transversale dans chaque chapitre tout le long de l'année)
- l'idée reçue que taper du Python sur calculatrice c'est pénible, particulièrement chez ceux qui ne le font pas justement, alors que les constructeurs ont fait plein d'efforts formidables (catalogue faisant qu'il suffit de choisir la fonction plutôt que de la saisir, indentation automatique, coloration syntaxique, autocomplétion, etc.)
- pour les éventuels élèves accrochant à l'enseignement du Python, vu qu'il s'agit ici d'un langage universel, la migration rapide vers d'autres plateformes autrement moins bridées pour leurs créations de projets, sautant donc complètement la case programmation sur calculatrice
Pour ce que nous pouvons constater, supprimer le langage
Basic sur
Graph Math+ est contre-productif. Cela ne va pas aider les élèves à faire davantage de
Python, bien au contraire. Cette suppression d'un langage autrement plus abordable va surtout les aider à moins programmer, en leur supprimant une chance de rentrer différemment dans le monde du codage, c'est-à-dire en s'affranchissant dans un premier temps de la notion de fonction.
Et pour finir, nous avons la suppression, à ce jour sans retour, des applications additionnelles que les développeurs les plus passionnés, jeunes ou moins jeunes, pouvaient coder en langage assembleur ou C. Nous pouvons citer, de façon tout sauf exhaustive, nombre d'applications
Graph 90+E de qualité professionnelle désormais inutilisables sur le modèle successeur
Graph Math+ :
- adaptation du logiciel de calcul littéral EigenMath
- KhiCAS, adaptation du logiciel intégré de calcul formel, mathématique et sciences Xcas pour ordinateurs
- Prizoop, émulateur de console de jeux Nintendo Game Boy Color
- Oiram, jeu à la Super Mario Bros 3
- Gravity Duck, portage du jeu Flash pour navigateurs
- CGDoom, portage des moteurs de jeu Doom et Doom 2 pour ordinateurs
- OutRun, adaptation du jeu d'arcade Sega
- NESizm, émulateur de console de jeux Nintendo NES
- jeu Bomberman
- jeu Super Mario 3D
- jeu Catylizm
- jeu Celeste, portage du jeu pour console virtuelle PICO-8
- portage du moteur de jeu OpenJazz Jackrabbit pour ordinateurs
Une activité certes non académique, rien à voir avec le langage
Python, mais ô combien de développeurs aujourd'hui professionnels ont découvert leur vocation en codant pour leur calculatrice
Casio au lycée ?
Cela fait vraiment beaucoup niveau suppressions, et même si nous comprenons les raisons c'est un peu trop brutal et extrême… Espérons que
Casio sera en mesure de nous entendre et faire un geste envers sa communauté… en revenant au moins sur ce dernier point.

 Comme Casio Espagne dès la rentrée 2019, pour la rentrée 2021 Casio Allemagne se lançait dans les coques en édition limitée pour calculatrices scientifiques conçues en partenariat avec des artistes.
Comme Casio Espagne dès la rentrée 2019, pour la rentrée 2021 Casio Allemagne se lançait dans les coques en édition limitée pour calculatrices scientifiques conçues en partenariat avec des artistes.
 Heureusement Casio a repris les visuels Classwiz Be Inspired, Change the Future 2021 pour des éditions limitées des modèles de dernière génération, mais dans d'autres pays que l'Allemagne.
Heureusement Casio a repris les visuels Classwiz Be Inspired, Change the Future 2021 pour des éditions limitées des modèles de dernière génération, mais dans d'autres pays que l'Allemagne.

 Rentrée 2022, Casio Allemagne a étendu sa collection Classwiz Be Inspired, Change the Future, avec une nouvelle série de 3 coques cette fois-ci sur le thème de la musique et du sport, toutes conçues en partenariat avec l'artiste Aleksander Gorgiev.
Rentrée 2022, Casio Allemagne a étendu sa collection Classwiz Be Inspired, Change the Future, avec une nouvelle série de 3 coques cette fois-ci sur le thème de la musique et du sport, toutes conçues en partenariat avec l'artiste Aleksander Gorgiev.

 Ici encore, Casio nous sort maintenant des éditions limitées avec le nouveau format de coque à clipser CW Classwiz, non seulement en Allemagne mais également dans d'autres pays.
Ici encore, Casio nous sort maintenant des éditions limitées avec le nouveau format de coque à clipser CW Classwiz, non seulement en Allemagne mais également dans d'autres pays.