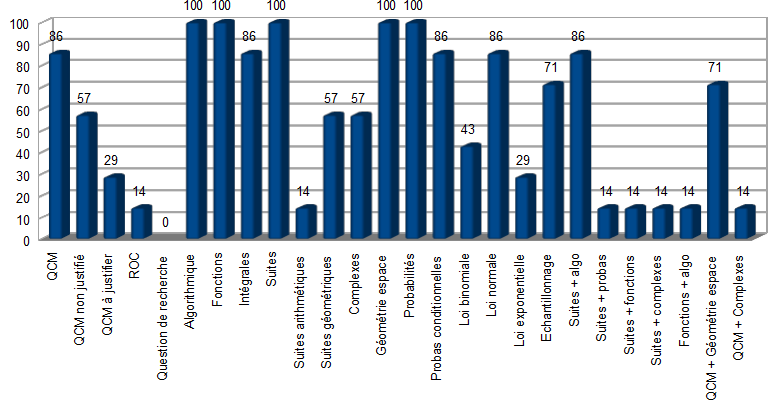
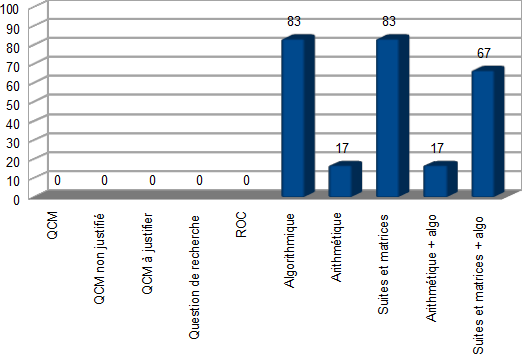
Intéressons-nous ce soir à l'algorithme tombé au sujet de Maths Obligatoire du BAC S 2013 en Antilles-Guyane, en exercice 4.
Il est assez particulier et donc intéressant; en effet il n'est pas seulement tombé avec une suite comme d'habitude, mais avec une suite complexe!

 Question A)3)a)
Question A)3)a)On nous demande donc une trace de l'algorithme avec l'état des variables à chaque itération de la boucle
(supposons que c'est à chaque fin d'itération de boucle - puisque l'énoncé ne précise pas).
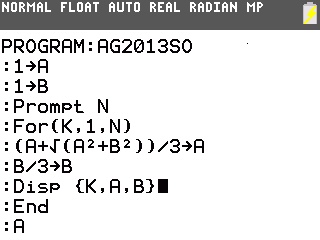
Il nous suffit pour cela de traduire l'algorithme en un programme pour notre calculatrice TI-76/82/83/84:
Rajoutons maintenant une simple instruction de sortie dans la boucle...
Et il n'y a plus qu'à recopier les résultats!

| K | A | B |
| 1 | 0,8047 | 0,3333 |
| 2 | 0,5586 | 0,1111 |
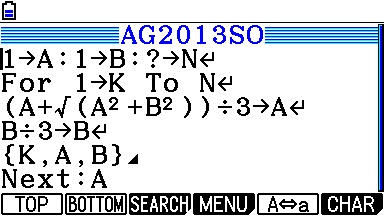
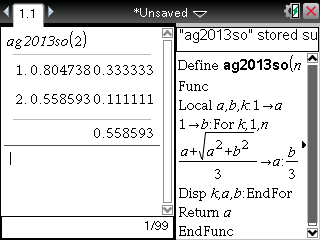
La même chose pouvait bien sûr s'obtenir à partir d'une Casio Graph/Prizm ou d'une TI-Nspire/89/92/V200:
Question A)3)b)L'énoncé définit donc une suite complexe z
n+1=(z
n+|z
n|)/3 avec z
0=1+i.
Cette suite complexe peut être modélisée par deux suites réelles a et b prenant respectivement les valeurs des parties réelles et imaginaires:
a
n+1=(a
n+√(a
n2+b
n2))/3 avec a
0=1
b
n+1=b
n/3 avec b
0=1
Ce sont ces suites qu'implémente l'algorithme, ces relations se retrouvant exactement dans les initialisations et affectations récurrentes sur A et B.
On pouvait aussi deviner en remarquant b
1=1/3 dans la trace précédente.
Comme l'algorithme se termine par un affichage de A, son but est d'afficher a
n, ou encore la partie réelle de z
n.
Lien:BAC S 2013 - Annales des sujets inédits toutes matières et corrections



 .
. .
.